Capítulo 1 Variables indicadoras (o dummies)
1.1 Ejemplos
1.1.1 Datos de atletas australianos
Los datos ais, de la libreria alr4, tienen información sobre 202 atletas australianos de élite (102 hombres y 100 mujeres). Se quiere evaluar la relación entre la concentración de hemoglobina (Hg, g/dl) y el índice de masa corporal (BMI, kg/m\(^2\)).
data(ais)
par(mfrow=c(1,2))
plot(density(ais$Hg[ais$Sex==0]),xlim=c(11,20),lwd=2,main = '',ylab='Densidad',xlab='Hg (g/dl)')
lines(density(ais$Hg[ais$Sex==1]),col=2,lwd=2)
plot(Hg~BMI,data=ais,col=ais$Sex+1,ylab='Hg (g/dl)',xlab='BMI')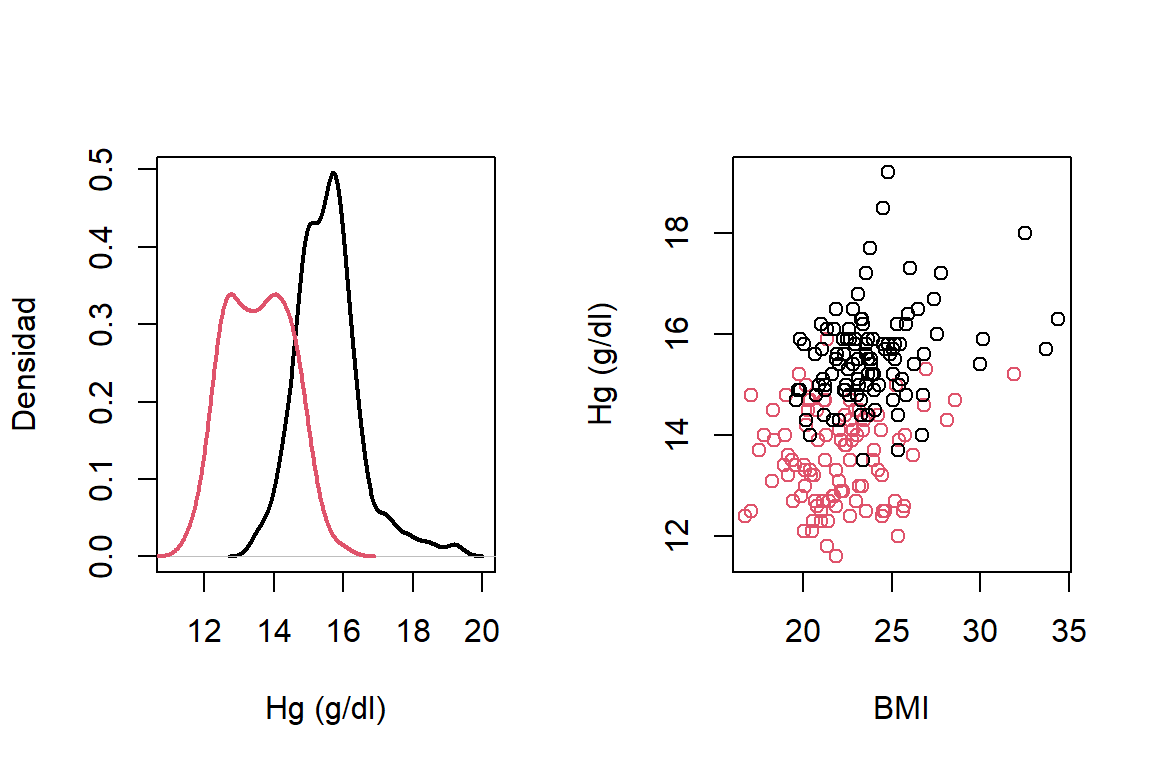
Figure 1.1: Datos de atletas. Densidad de la hemoglobina para hombres y mujeres (derecha) y diagrama de dispersión entre la homoglobina y el índice de masa corporal (izquierda). Negro para hombres y rojo para mujeres.
En la Figura 1.1 (izquierda) vemos que los niveles de hemoglobina son mayores para hombres que para mujeres. En la Figura 1.1 (derecha) observamos que hay una relación positiva entre la hemoglobina y el índice de masa corporal tanto para hombres como para mujeres. Esto nos puede indicar que ingresar el sexo del atleta en el modelo puede mejorarnos el ajuste.
1.1.2 Datos de la ONU
Retomemos los datos de la ONU (UN11 de la librería alr4). Las variables de interés son:
- fertility: Número esperado de nacidos vivos por mujer.
- ppgdp: producto nacional bruto per cápita (PNB, en dólares).
- Purban: el porcentaje de la población que vive en un área urbana.
- lifeExpF: esperanza de vida femenina (años).
- group: si el país pertenece a la OCDE (Organización para la Cooperación y el Desarrollo Económicos), África o otros.
Por ahora consideremos la relación entre la fertilidad y el PNB per cápita, teniendo en cuenta el grupo al que pertenece cada país.
data(UN11)
plot(log(fertility)~log(ppgdp),data=UN11,col=UN11$group,xlab='log PNB per cápita (dólares)', ylab='log # esperado de nacidos vivos por mujer')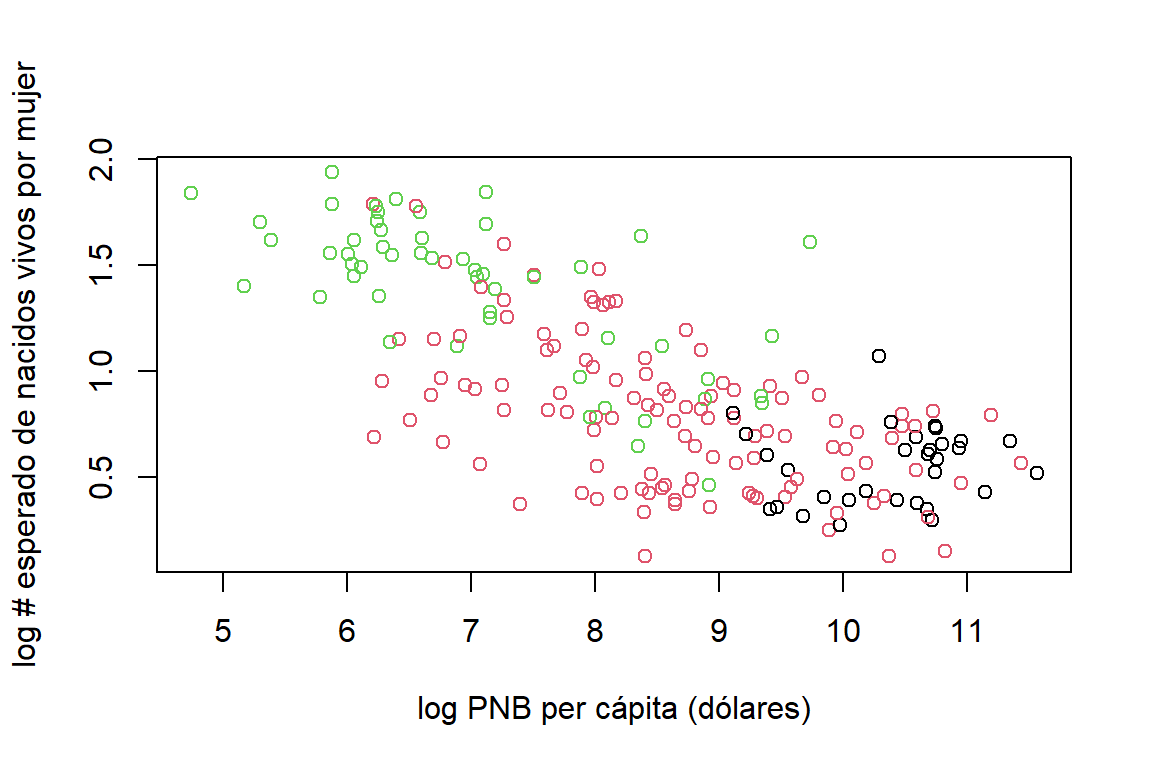
Figure 1.2: Datos de la ONU. Relación entre la fertilidad y el PNB per cápita para los países de OCDE (puntos negros), países africanos (puntos verdes) y los otros países (rojos)
En la Figura 1.2 podemos observar que, en general, cuando el PNB aumenta, la tasa de fertilidad disminuye. Sin embargo, esta relación puede variar según la categoría del país. Para los países de la OCDE, esta relación no es fuerte. Mientras que para los demás se mantiene esta relación negativa. Por esta razón sería de gran importancia incluir esta variable categórica dentro del modelo.
1.2 Variables indicadoras
Las covariables categóricas entran en un modelo como variables indicadoras (o también llamadas dummies). En el caso que la covariable \((X)\) tenga dos categorías, entonces se crea una variable indicadora. Por ejemplo, para los datos de los atletas, el sexo requiere una indicadora: \[ u_{i} = \begin{cases} 1 & \mbox{ si la observación i es de una mujer}, \\ 0 & \mbox{ si la observación i es de un un hombre}. \\ \end{cases} \] Aquí la categoría hombre es llamada la categoría de referencia.
En caso que la covariable categórica tenga \(K\) categorías, se tienen que crear \(K-1\) variables indicadoras. Por ejemplo, para la variable grupo de país en los datos de la ONU se requieren 2 variables indicadoras \((u_{1} y u_{2})\) como lo muestra la Tabla 1.1. En este caso, la categoría de referencia es OECD.
| Categoría | \(u_{1}\) | \(u_{2}\) |
|---|---|---|
| OECD | 0 | 0 |
| otro | 1 | 0 |
| África | 0 | 1 |
1.2.1 Modelos con covariables categóricas
Suponga que se quiere ajustar un modelo para una variable respuesta \(Y\) en función de dos covariables: una continua \(X\) y una indicadora \(Z\) (es decir una variable categórica con dos 2 categorías). El modelo propuesto es el siguiente: \[\begin{equation} y_{i} = \beta_{0} + x_{i}\beta_{1} + z_{i}\beta_{2} + x_{i}z_{i}\beta_{3} + \varepsilon_{i}, \tag{1.1} \end{equation}\] donde \(\varepsilon_{i} \sim N(0,\sigma^{2})\). Tenemos que, si \(z_i=0\): \[ E(Y | X=x_i, Z=0) = \beta_{0} + x_{i}\beta_{1}. \] Mientras que, si \(z_i=1\): \[ E(Y | X=x_i, Z=1) = (\beta_{0}+\beta_{2}) + x_{i}(\beta_{1}+\beta_{3}). \] Por lo que el modelo (1.1) genera dos rectas, una para cada categoría. \(\beta_2\) indica la diferencia de intercepto entre las dos categorías y \(\beta_3\) la diferencia entre pendientes. En la Figura 1.3(izquierda) se observan las dos rectas que se obtienen a partir de este modelo. Si se elimina la interacción entre variables (es decir, \(\beta_3=0\)), se obtienen dos rectas paralelas (Figura 1.3, derecha).
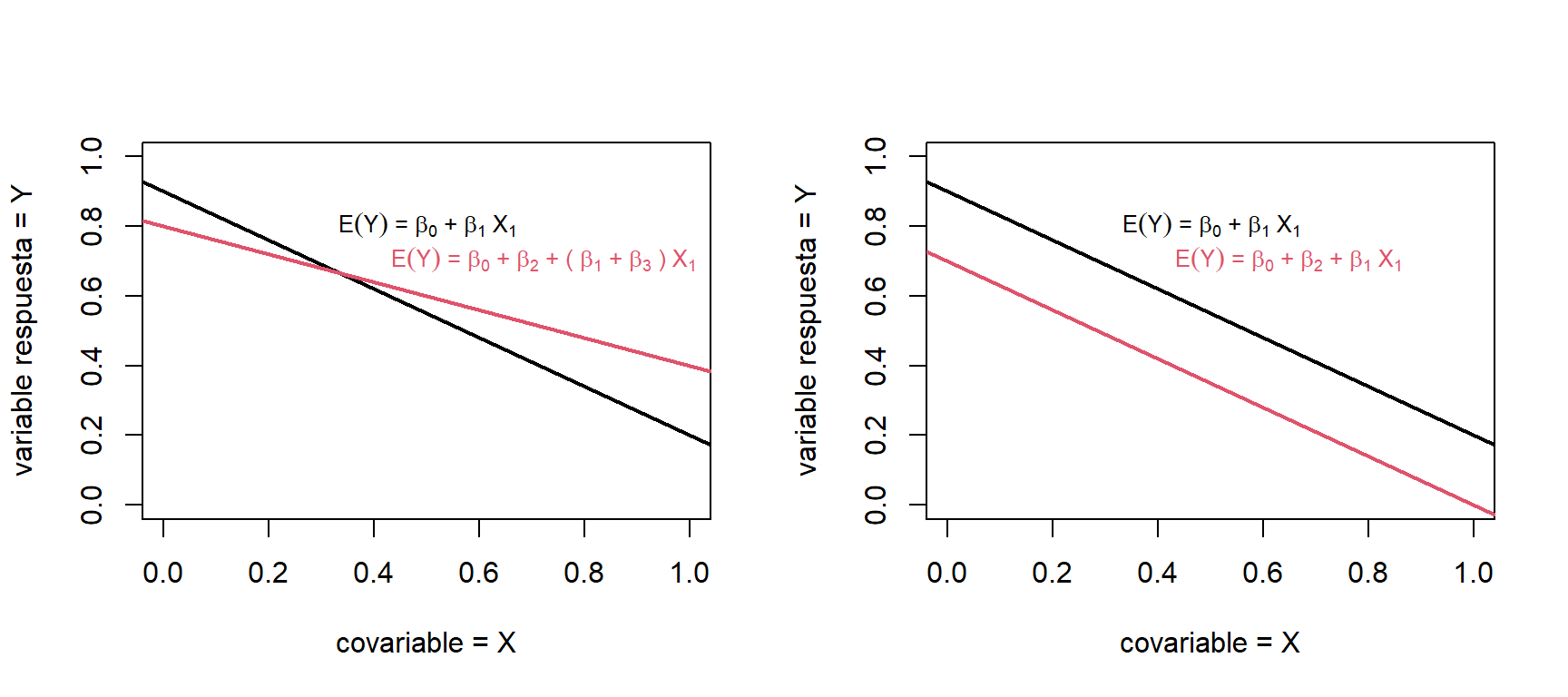
Figure 1.3: Efecto de la interacción entre variable continua e indicadora. Modelo general (izquierda) y modelo de líneas paralelas (derecha).
Hay que tener en cuenta que la asignación de la categoría de referencia no afecta en nada al ajuste del modelo. Sin embargo, la interpretación de los coeficientes cambia.
1.2.2 Modelo para los datos de atletas australianos
Para los datos de los atletas, se sugiere el siguiente modelo:
\[\begin{equation}
\begin{split}
\mbox{Hg}_{i} =& \beta_{0} + \mbox{Sex}_{i}\beta_{1} + \mbox{BMI}_{i}\beta_{2} + \mbox{Sex}_{i}\mbox{BMI}_{i}\beta_{3} + \varepsilon_{i},
\end{split}
\nonumber
\end{equation}\]
donde:
\[
\mbox{Sex}_{i} = \begin{cases}
1 & \mbox{ si la observación i corresponde a una mujer}, \\
0 & \mbox{ de otra forma}. \\
\end{cases}
\]
Note que en la base de datos ais, la variable sex ya está codificada de esta forma. Si la variable no está codificada de forma numérica, R eligirá la categoría de referencia de forma automática. Sin embargo, esta puede modificarse con la función relevel().
Para ajustar el modelo utilizamos la función lm (aquí estamos incluyendo los efectos de BMI y Sex, así como la interacción):
##
## Call:
## lm(formula = Hg ~ Sex * BMI, data = ais)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.9997 -0.6625 -0.0478 0.5784 3.5583
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 13.21316 0.78662 16.797 <2e-16 ***
## Sex -0.66140 1.09835 -0.602 0.5477
## BMI 0.09788 0.03269 2.994 0.0031 **
## Sex:BMI -0.05203 0.04761 -1.093 0.2758
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9092 on 198 degrees of freedom
## Multiple R-squared: 0.5613, Adjusted R-squared: 0.5546
## F-statistic: 84.44 on 3 and 198 DF, p-value: < 2.2e-16Tenemos que \(\widehat{\beta}_{2} =0.1\), lo que nos indica que el valor esperado del nivel de hemoglobina aumenta en \(0.1\) g/dl por cada aumento unitario en el índice de masa corporal de los hombres. Para las mujeres, el efecto del índice de masa corporal sobre el nivel de hemoglobina también es positivo, pero con una pendiente menor \(\widehat{\beta}_{2} +\widehat{\beta}_{3} = 0.1 - 0.05 = 0.05\).
La representación gráfica del modelo se puede observar en la Figura 1.4. Aquí vemos que la pendiente para las mujeres es un poco menor que para los hombres.
plot(Hg~BMI,data=ais,col=ais$Sex+1,ylab='Hg (g/dl)',xlab='BMI')
abline(a=mod.ais$coefficients[1],b=mod.ais$coefficients[3],lwd=2)
abline(a=mod.ais$coefficients[1]+mod.ais$coefficients[2],b=mod.ais$coefficients[3]+mod.ais$coefficients[4],col=2,lwd=2)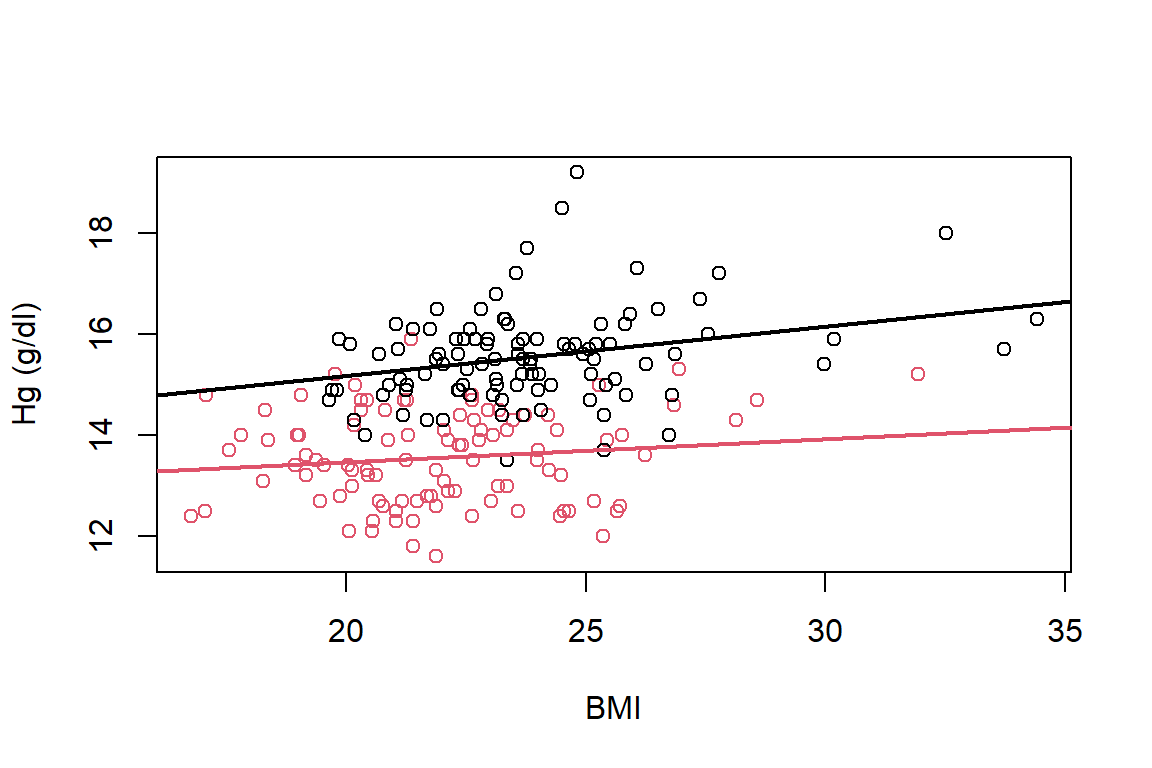
Figure 1.4: Datos de atletas. Ajuste del modelo para la homoglobina en función del índice de masa corporal y sexo. Línea negra para hombres y línea roja para mujeres.
Si miramos la significancia del \(\widehat{\beta}_3\) (valor-\(p\) igual a 0.276), podemos concluir que las diferencias en pendiente no son significativas. Por lo que, el efecto del índice de masa corporal sobre los niveles de hemoglobina es el mismo para mujeres que para hombres.
Si queremos evaluar si los niveles de hemoglobina son iguales para hombres y mujeres, debemos evaluar la siguiente hipótesis:
\[
H_{0}: \beta_{1} = \beta_3 = 0.
\]
En R, esto lo podemos realizar usando la función anova() (la cuál realiza una prueba F) comparando el modelo completo contra el modelo reducido sin la variable Sex:
## Analysis of Variance Table
##
## Model 1: Hg ~ BMI
## Model 2: Hg ~ Sex * BMI
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 200 318.52
## 2 198 163.69 2 154.82 93.637 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Vemos que se rechaza \(H_0\), es decir que hay diferencias en los niveles de homoglobina entre hombres y mujeres. \(\beta_1\) o \(\beta_3\) es diferente de cero, pero no ambos (esto por los resultados del modelo completo). Eliminando la interacción obtenemos un modelo con lineas paralelas: \[ \mbox{Hg}_{i} = \beta_{0} + \mbox{Sex}_{i}\beta_{1} + \mbox{BMI}_{i}\beta_{2} + \varepsilon_{i}, \] donde \(\varepsilon_{i} \sim N(0, \sigma^{2})\), y se calcula de la siguiente forma:
##
## Call:
## lm(formula = Hg ~ Sex + BMI, data = ais)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.0131 -0.6530 -0.0263 0.6249 3.5806
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 13.79954 0.57549 23.979 < 2e-16 ***
## Sex -1.85251 0.13587 -13.634 < 2e-16 ***
## BMI 0.07335 0.02378 3.085 0.00233 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9097 on 199 degrees of freedom
## Multiple R-squared: 0.5586, Adjusted R-squared: 0.5542
## F-statistic: 125.9 on 2 and 199 DF, p-value: < 2.2e-16La estimación del efecto asociado al sexo indica la diferencia media del nivel de hemoglobina entre hombres y mujeres. En la Figura 1.5 vemos que el modelo de líneas paralelas tiene casi el mismo ajuste que el modelo general.
plot(Hg~BMI,data=ais,col=ais$Sex+1,ylab='Hg (g/dl)',xlab='BMI')
abline(a=mod.ais$coefficients[1],b=mod.ais$coefficients[3],lwd=2)
abline(a=mod.ais$coefficients[1]+mod.ais$coefficients[2],b=mod.ais$coefficients[3]+mod.ais$coefficients[4],col=2,lwd=2)
abline(a=mod.ais.lp$coefficients[1],b=mod.ais.lp$coefficients[3],lwd=2,lty=2)
abline(a=mod.ais.lp$coefficients[1]+mod.ais.lp$coefficients[2],b=mod.ais.lp$coefficients[3],col=2,lwd=2,lty=2)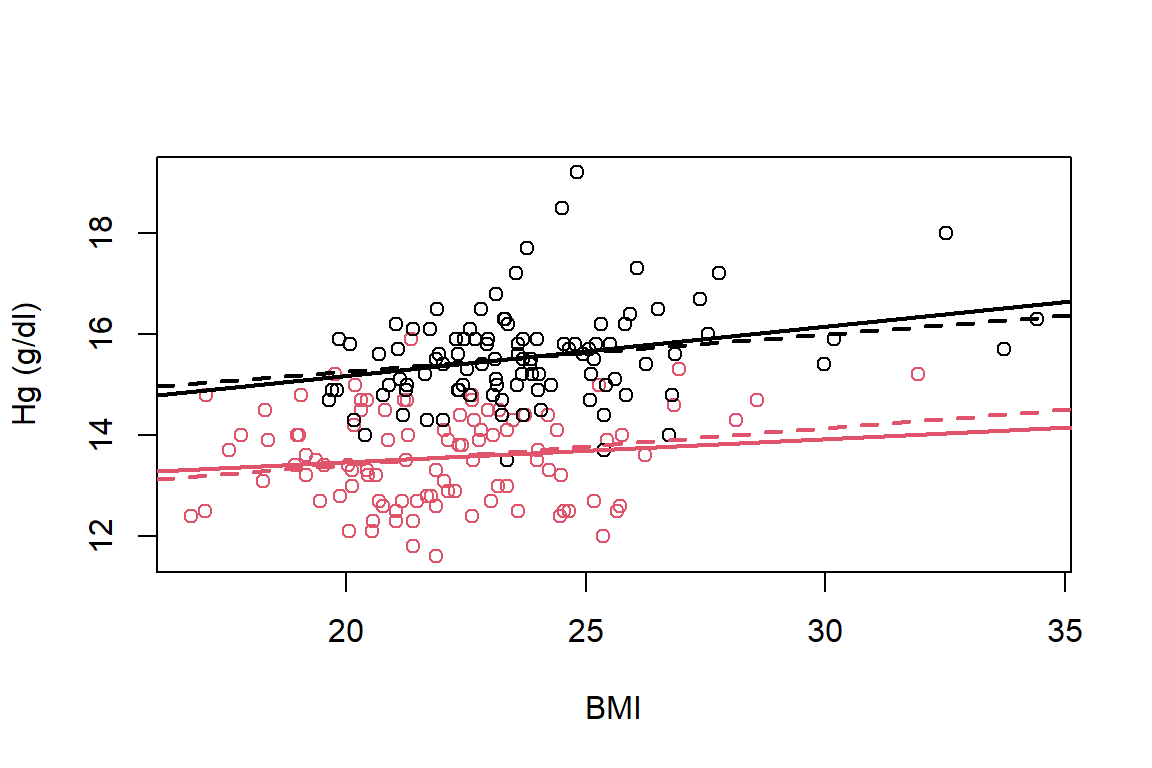
Figure 1.5: Datos de atletas. Ajuste del modelo general (línea solida) y el modelo líneas paralelas (línea discontinua) para la homoglobina en función del índice de masa corporal y sexo. Líneas negra para hombres y líneas roja para mujeres.
En conclusión, hay diferencia en los niveles de hemoglobina entre hombres y mujeres (es, en promedio, mayor para lo hombres en 1.85g/dl). Sin embargo, el efecto del índice de masa corporal es el mismo para ambos sexos.
1.2.3 Modelo para los datos de la ONU
El modelo propuesto es el siguiente: \[\begin{equation} \begin{split} \log\mbox{fertility}_{i} =& \beta_{0} + \mbox{u}_{1i}\beta_{1}+\mbox{u}_{2i}\beta_{2} + \log\mbox{ppgdp}_{i}\beta_{3} + \\ & \mbox{u}_{1i}\log\mbox{ppgdp}_{i}\beta_{4} + \mbox{u}_{2i}\log\mbox{ppgdp}_{i}\beta_{5} + \varepsilon_{i}, \end{split} \nonumber \end{equation}\] donde: \[ \mbox{u}_{1i} = \begin{cases} 1 & \mbox{ si el país i pertenece a la categoría otro}, \\ 0 & \mbox{ de otra forma}, \\ \end{cases} \mbox{ y } \mbox{u}_{2i} = \begin{cases} 1 & \mbox{ si el país i pertenece a África}, \\ 0 & \mbox{ de otra forma}. \\ \end{cases} \] Por lo tanto, OECD es la categoría de referencia. El modelo ajustado es:
##
## Call:
## lm(formula = log(fertility) ~ group * log(ppgdp), data = UN11)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.69358 -0.16963 0.02005 0.16838 0.73633
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.21836 0.81290 0.269 0.78851
## groupother 1.87888 0.83290 2.256 0.02520 *
## groupafrica 2.54072 0.84299 3.014 0.00293 **
## log(ppgdp) 0.03217 0.07832 0.411 0.68170
## groupother:log(ppgdp) -0.18418 0.08106 -2.272 0.02417 *
## groupafrica:log(ppgdp) -0.22637 0.08430 -2.685 0.00788 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2739 on 193 degrees of freedom
## Multiple R-squared: 0.6305, Adjusted R-squared: 0.6209
## F-statistic: 65.86 on 5 and 193 DF, p-value: < 2.2e-16A partir de estos resultados obtenemos tres rectas que describen el valor esperado del logarítmo de la fertilidad en función del logarítmo del PNB per cápita, una para cada tipo de país. Para los países de la OCDE, tenemos que: \[ E(\log\mbox{fertility}) = 0.218 + 0.032\log \mbox{ppgdp}. \] Para los países Africanos: \[ E(\log\mbox{fertility}) = 2.759 -0.194\log \mbox{ppgdp}. \] Finalmente, para los otros países: \[ E(\log\mbox{fertility}) = 2.097 -0.152\log \mbox{ppgdp}. \] Aquí vemos que para los países que no son de la OCDE, el PNB tiene un efecto negativo significativo sobre la tasa de fertilidad. Mientras que para los países de la OCDE, este efecto es positivo, aunque no es significativo. Esto mismo lo podemos ver gráficamente en la Figura 1.6.
Beta.UN11 = mod.UN11$coefficients
plot(log(fertility)~log(ppgdp),data=UN11,col=UN11$group,xlab='log PNB per cápita (dólares)', ylab='log # esperado de nacidos vivos por mujer')
abline(a=Beta.UN11[1],b=Beta.UN11[4],lwd=2)
abline(a=Beta.UN11[1]+Beta.UN11[2],b=Beta.UN11[4]+Beta.UN11[5],col=2,lwd=2)
abline(a=Beta.UN11[1]+Beta.UN11[3],b=Beta.UN11[4]+Beta.UN11[6],col=3,lwd=2)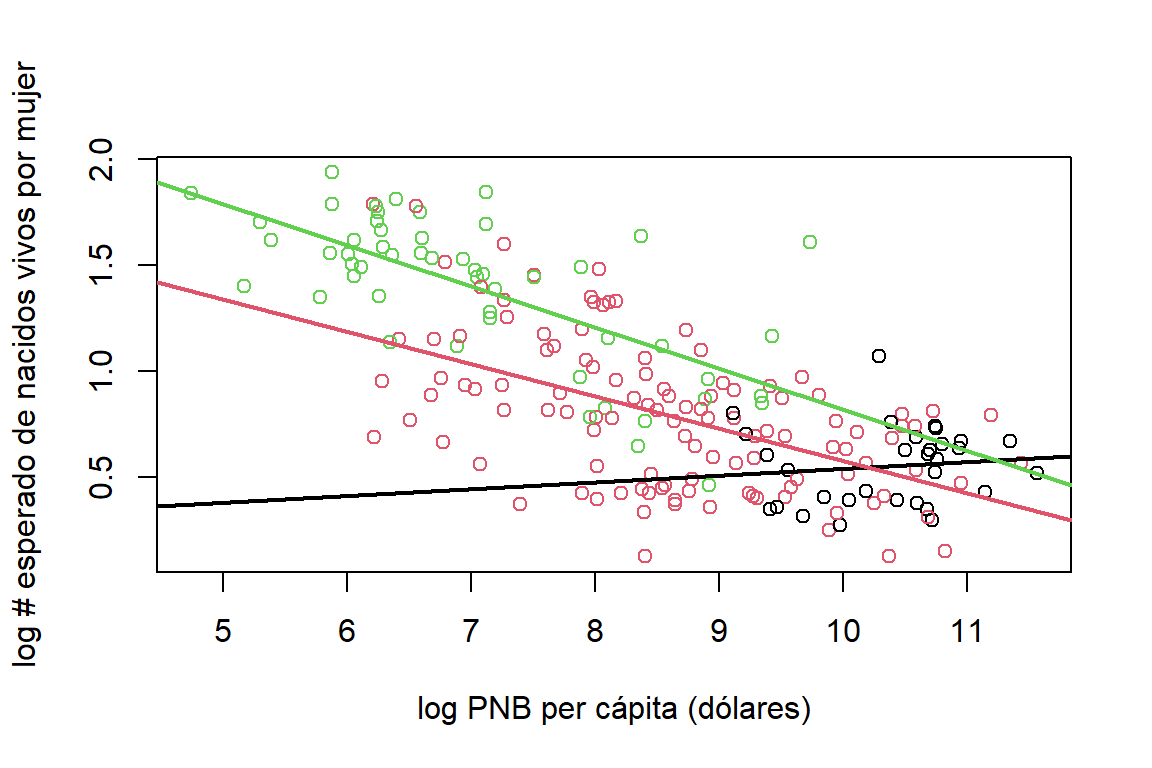
Figure 1.6: Datos de la ONU. Ajuste del modelo para la fertilidad en función del PNB y tipo de país. Países de OCDE (línea negra), países africanos (línea verde) y los otros países (línea roja)
Usando la función relevel() se puede cambiar la categoría de referencia. Por ejemplo, si queremos que la categoría de referencia sea other:
UN11.alt = UN11
UN11.alt$group = relevel(UN11.alt$group,ref ='other')
mod.UN11.alt = lm(log(fertility)~group*log(ppgdp), data=UN11.alt)
summary(mod.UN11.alt)Note que cambiar la categoría de referencia no altera en nada los resultados del ajuste. Solo cambian la interpretación de los coeficientes.
Se podría hacer la siguiente pregunta, ¿el efecto del PNB sobre la fertilidad es el mismo para cada tipo de país?. Para resolver esta pregunta, se plantea la siguiente hipótesis:
\[
H_0: \beta_4 = \beta_5 = 0.
\]
El estadístico de prueba lo podemos obtener usando la función anova() (prueba F) en R:
## Analysis of Variance Table
##
## Model 1: log(fertility) ~ group + log(ppgdp)
## Model 2: log(fertility) ~ group * log(ppgdp)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 195 15.033
## 2 193 14.484 2 0.54848 3.6542 0.02769 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Este resultado indica que hay evidencia suficiente para concluir que el efecto del PNB sobre la fertilidad no es el mismo para cada tipo de país.
Ahora, podríamos preguntarnos: ¿las pendientes son las mismas para las categorías de otro y África?. Para esto, se plantea la siguiente hipótesis: \[ H_0: \beta_4 = \beta_5. \] También se puede expresar de la siguiente forma: \[ H_{0}: \boldsymbol L\boldsymbol \beta= \begin{pmatrix} 0 & 0 & 0 & 0 & 1 & -1 \end{pmatrix} \begin{pmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \\ \beta_3 \\ \beta_4 \\ \beta_5 \end{pmatrix} = 0 \] Esto, en R es:
## Linear hypothesis test
##
## Hypothesis:
## groupother:log(ppgdp) - groupafrica:log(ppgdp) = 0
##
## Model 1: restricted model
## Model 2: log(fertility) ~ group * log(ppgdp)
##
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 194 14.579
## 2 193 14.484 1 0.094808 1.2633 0.2624Dado que no se rechaza \(H_0\), el efecto del PNB sobre la fertilidad es el mismo para los países Africanos y los de la categoría de otros.
En resumen, a partir del análisis de regresión se tiene que: el efecto del PNB per cápita sobre la fertilidad depende del tipo de país. Para los países miembros de la OECD, no hay un efecto significativo. Sin embaro, para los demás países, el efecto es negativo (y no es significativamente diferente para las categorías de África y otros).