Capítulo 2 Modelos polinomiales

2.1 Ejemplos

2.1.1 Pasteles

Con los datos cakes de la libreria alr4 se tienen dos objetivos. Primero, evaluar el efecto de la temperatura y tiempo de horneado sobre la palatabilidad de mazclas de pasteles para hornear. Segundo, encontrar la combinación de estos factores que maximizan la palatabilidad. Como variable respuesta (Y) se tiene el promedio de calificación de la palatabilidad de cuatro pasteles horneados. Mientras que las covariables son: el tiempo de horneado (X1, en minutos) y la temperatura (X2, en grados Fahrenheit)

library(alr4)
data(cakes)
plot(cakes[,-1])

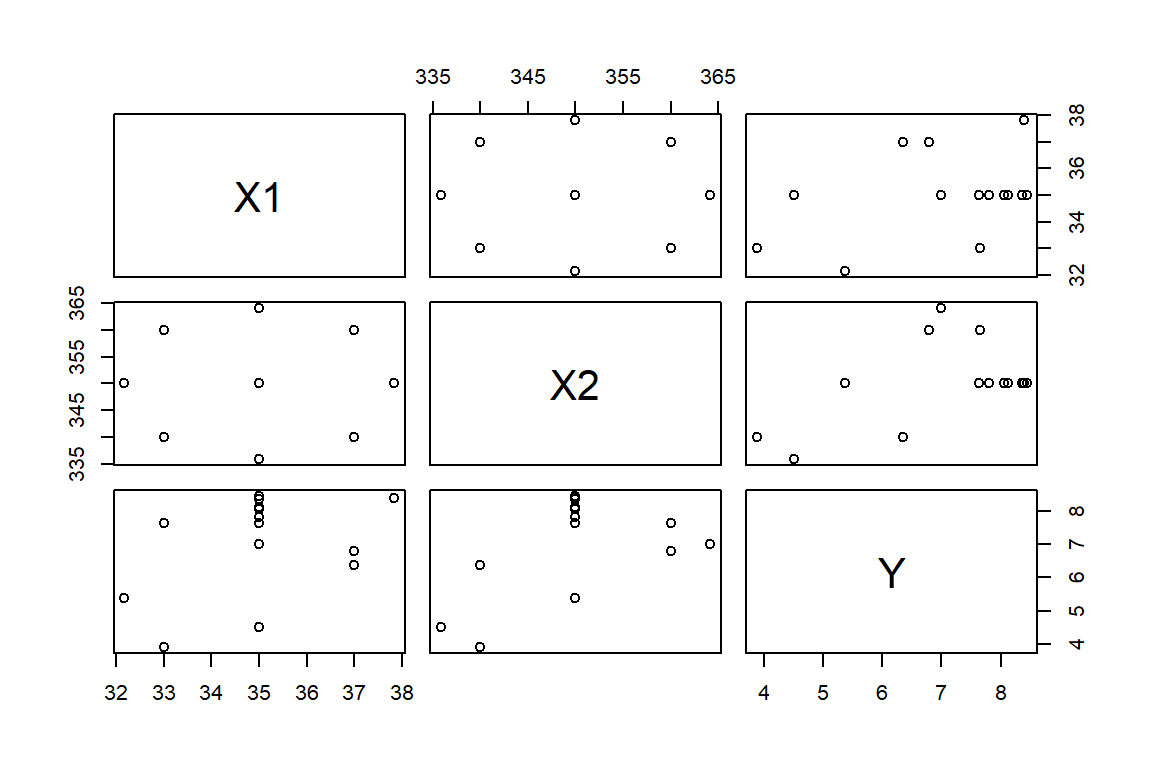
Figure 2.1: Datos de pasteles. Diagrama de dispersión.

2.1.2 Datos de Boston

La base de datos Boston de la libreria MASS contiene información sobre 506 suburbios del area metropolitana de Boston. El objetivo del estudio es evaluar la relación del precio de las viviendas y la concentración de contaminación ambiental. En esta sección evaluaremos la relación entre la concentración anual de óxido de nitrógeno (\(y\), en partes por diez millones) y la distancia a cinco centros de empleo.

library(MASS)
data(Boston)
plot(nox~dis,data=Boston,ylab='NOx',xlab='distancia a centros de empleo')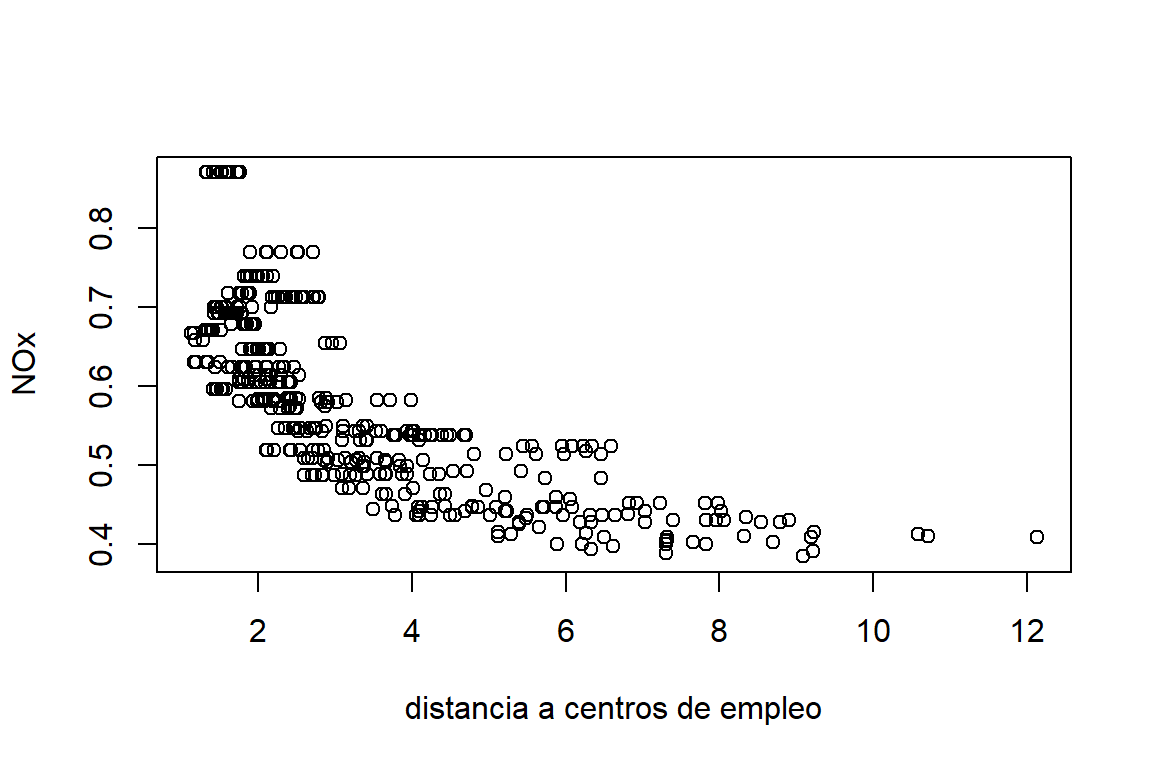

Figure 2.2: Datos de Boston. Relación entre el óxido de nitrógeno y la distancia a centros de empleo.

2.2 Modelos polinomiales

Considere el modelo: \[ y_{i} = \beta_{0} + \beta_{1}x_{i} + \varepsilon_i, \] donde \(\varepsilon_i \sim N(0,\sigma^2)\) y \(cov(\varepsilon_i,\varepsilon_j)=0\) para todo \(i\neq j\). Este describe la relación lineal entre \(y\) y \(x_1\). Si las relación entre las variables presentan curvaturas, se puede considerar un modelo polinómico de la forma: \[ y_{i} = \beta_{0} + \beta_{1}x_{i} + \beta_{2}x_{i}^{2} + \ldots + \beta_{r}x_{i}^{r} + \varepsilon_i. \] Este modelo se sigue considerando como un modelo lineal, dado que es lineal en los parámetros (es una función lineal de \(\boldsymbol \beta\)). En la Figura 2.3 se puede observar diferentes curvas para modelos lineales (orden 1), cuadráticos (orden 2) y cúbicos (orden 3). Aquí vemos que este tipo de modelos son muy versatiles. Cualquier función suave se puede ajustar meidante un polinomio de grado suficientemente alto. Por esta razón, los modelos polinomicos son usados en casos donde las relaciones entre las variables son no-lineales y se pueden aproximar por un polinomio.

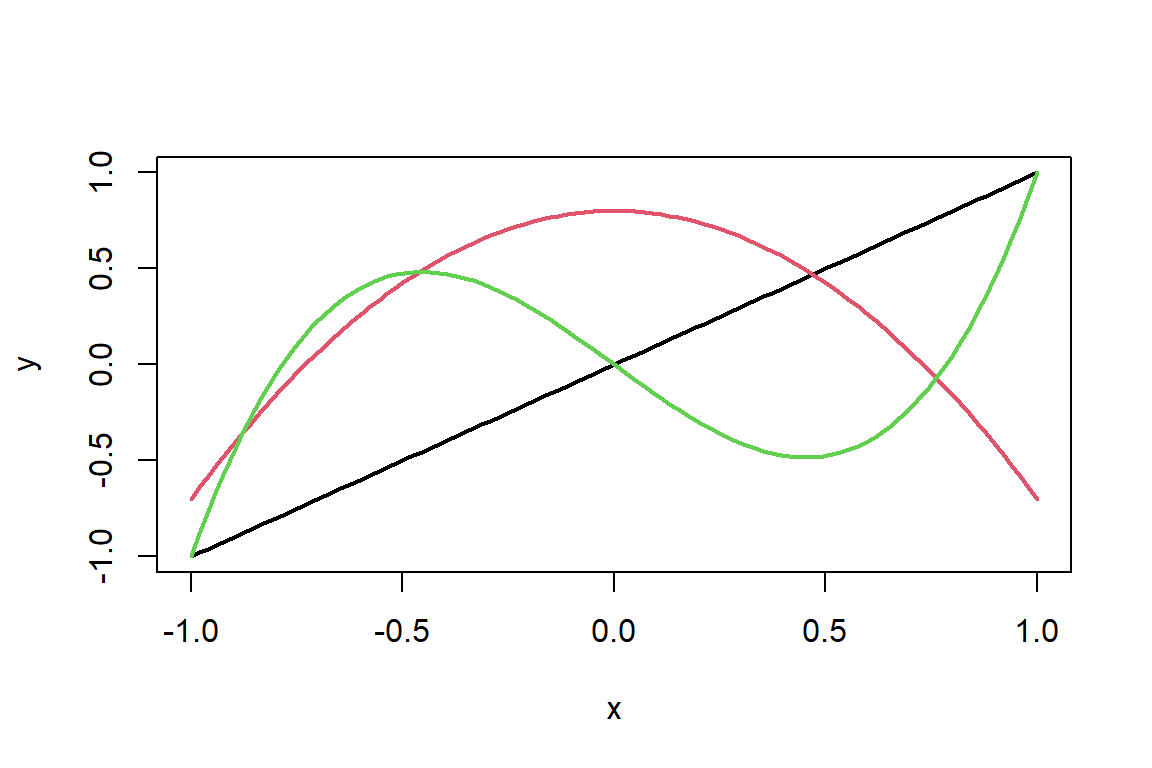
Figure 2.3: Polinomio de grado 1 (linea negra), grado 2 (linea roja) y grado 3 (linea verde).

En el caso que se tengan dos covariables, un modelo de orden 2 se expresa de la forma: \[ y_{i} = \beta_{0} + \beta_{1}x_{1i} + \beta_{2}x_{2i} + \beta_{3}x_{1i}^2 + \beta_{4}x_{2i}^2 + \beta_{5}x_{1i}x_{2i} + \varepsilon_i. \] En las Figuras 2.4-2.6 muestran el valor esperado de \(Y\) en un modelo lineal (asumiendo \(\beta_3=\beta_4=\beta_5=0\)), con interacción (\(\beta_3=\beta_4=0\)) y cuadrático.

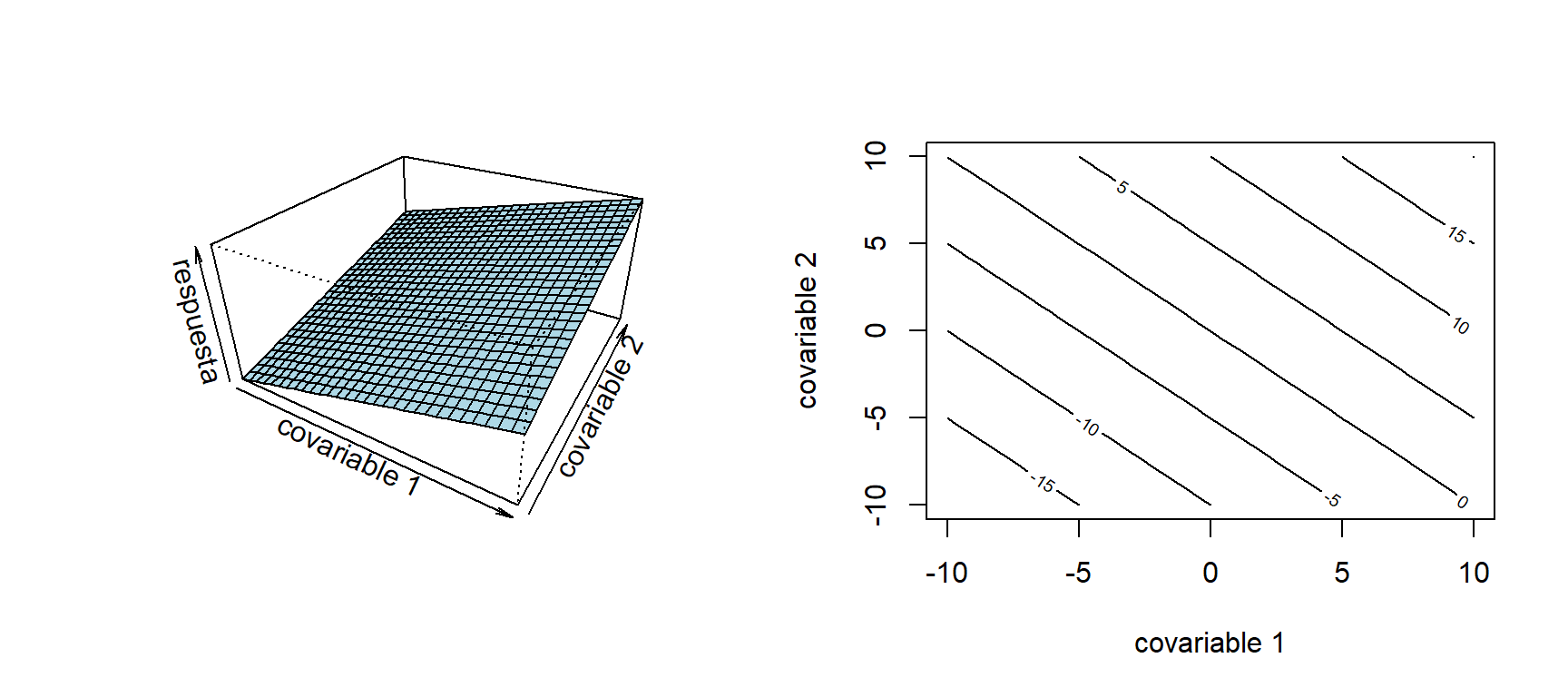
Figure 2.4: Valor esperado de \(Y\) en un modelo lineal (izquierda) y gráfico de contorno (derecha).

El número de parámetros incrementa rápidamente con el número de covariables. Con \(k\) covariables, tenemos: un intercepto, \(k\) términos lineales, \(k\) términos cuadráticos, y \(k(k - 1)/2\) interacciones. Por esta razón, en muchos casos, no se toman en cuentas las interacción cuando el número de covariables es grande.

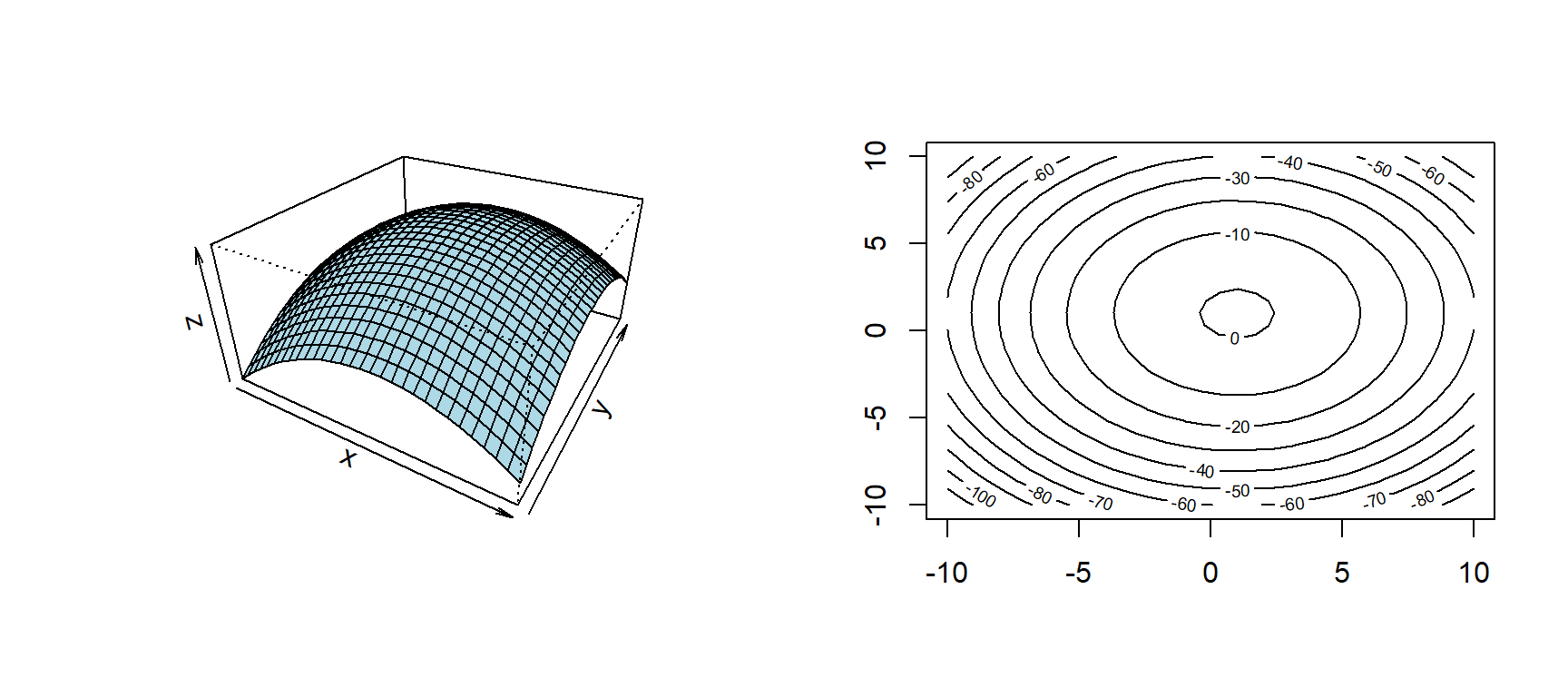
Figure 2.5: Valor esperado de \(Y\) en un modelo cuadrático (izquierda) y gráfico de contorno (derecha).

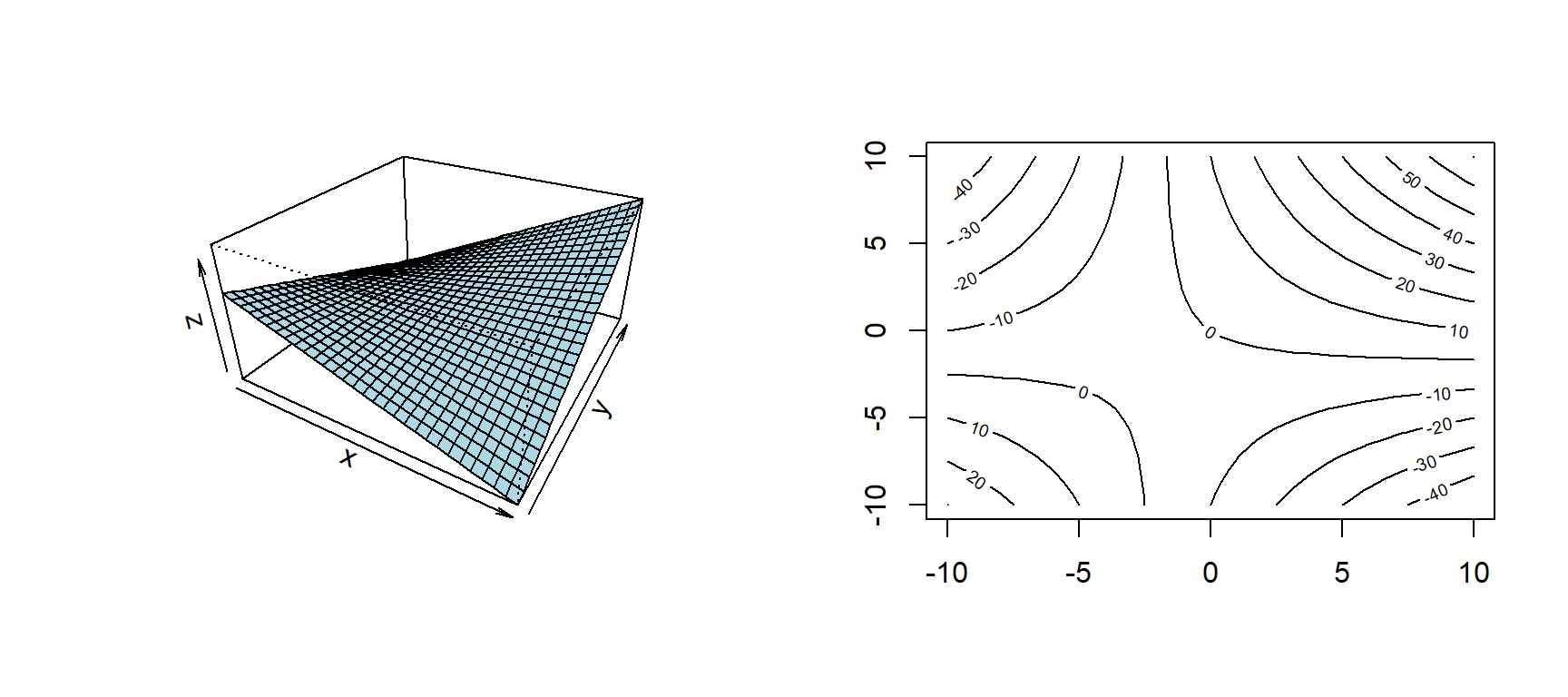
Figure 2.6: Valor esperado de \(Y\) en un modelo lineal con interacción (izquierda) y gráfico de contorno (derecha).

Hay aspectos que se deben tener en la práctica cuando se implementa un modelo polinomial:

Selección del orden: La idea es mantener el orden del polinomio bajo. Si embargo, si es muy bajo no logra capturar la curvatura presente en los datos. En caso que el orden sea grande, el modelo es innecesariamente más complejo y puede haber problemas de multicolinealidad.

Si los datos exige un modelo de orden alto \((k > 3)\), se pueden hacer transformación sobre las variables, y así, poder ajustar un modelo polinomial de orden bajo (por ejemplo cuadrático).

La selección del orden puede hacerse de dos formas. (1) Hacia delante: empezar con un modelo de orden \(1\) e incrementar el orden uno a uno hasta que un término mayor ya no sea significativo. Hacia atrás: empezar con el modelo más complejo y eliminar los términos mayores uno a uno hasta que todos sean significativos.

Extrapolación: La extrapolación con modelos polinomiales puede ser muy peligrosa. Por ejemplo en la Figura 2.7 podemos ajustar un modelo de orden dos a los datos (linea negra). Si hacemos una predicción fuera del rango de los datos, el valor esperado predicho sigue el comportamiento cuadrático propuesto. Sin embargo, el valor esperado de \(Y\) puede seguir un comportamiento diferente (linea roja discontinua). Lo que lleva a tener una predicción sesgada.

Figure 2.7: Problema de extrapolación.

Multicolinealidad: Al aumentar el polinomio, la matriz \(\boldsymbol X'\boldsymbol X\) se vuelve mal acondicionada. Es decir, las estimaciones pueden ser inestables y los errores estándar se inflan. Este problema se puede solucionar centrando las covariables. Por ejemplo en un modelo de orden 2: \[ E(Y | X=x) = \beta_{0} + \beta_{1}(x-\bar{x}) + \beta_{2}(x-\bar{x})^{2}. \] Otra solución es usando polinomios ortogonales.

2.2.1 Interpretación de los coeficientes

Considere un modelo de orden 2. El valor esperado de \(Y\) está dado por: \[ E(Y| X_{1}=x_1,X_{2}=x_2) = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \beta_{3}x_{1}^{2} + \beta_{4}x_{2}^{2} + \beta_{5}x_{1}x_{2}. \] Si \(x_{1}\) cambia en \(\delta\) unidades \((x_{1} + \delta)\), tenemos que: \[ E(Y| X_{1}=x_1+\delta,X_{2}=x_2) = \beta_{0} + \beta_{1}(x_{1}+\delta) + \beta_{2}x_{2} + \beta_{3}(x_{1} + \delta)^{2} + \beta_{4}x_{2}^{2} + \beta_{5}(x_{1}+\delta)x_{2}. \] Ahora calculando la diferencia: \[ E(Y| X_{1}=x_1+\delta,X_{2}=x_2) - E(Y| X_{1}=x_1,X_{2}=x_2) = (\beta_{1}\delta + \beta_{3}\delta^{2}) + 2\beta_{3}\delta x_{1} + \beta_{5}\delta x_{2}. \] Note que el efecto del cambio \(\delta\) en \(X_1\) depende de ambas covariables y del valor de \(\delta\). Por esta razón, la interpretación de los coeficientes es complicada.

2.2.2 Pasteles

Para los datos de los pasteles, se propone el siguiente modelo: \[ y_{i} = \beta_{0} + \beta_{1}x_{1i} + \beta_{2}x_{2i} + \beta_{3}x_{1i}^2 + \beta_{4}x_{2i}^{2} + \beta_{5}x_{1i}x_{2i} + \varepsilon_{i}. \] El ajuste del modelo es:

mod.cakes = lm(Y ~ X1*X2 + I(X1^2)+I(X2^2),data=cakes)
summary(mod.cakes)

## 
## Call:
## lm(formula = Y ~ X1 * X2 + I(X1^2) + I(X2^2), data = cakes)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.4912 -0.3080  0.0200  0.2658  0.5454 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -2.204e+03  2.416e+02  -9.125 1.67e-05 ***
## X1           2.592e+01  4.659e+00   5.563 0.000533 ***
## X2           9.918e+00  1.167e+00   8.502 2.81e-05 ***
## I(X1^2)     -1.569e-01  3.945e-02  -3.977 0.004079 ** 
## I(X2^2)     -1.195e-02  1.578e-03  -7.574 6.46e-05 ***
## X1:X2       -4.163e-02  1.072e-02  -3.883 0.004654 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4288 on 8 degrees of freedom
## Multiple R-squared:  0.9487, Adjusted R-squared:  0.9167 
## F-statistic:  29.6 on 5 and 8 DF,  p-value: 5.864e-05

Además, los factores de inflación de varianza son los siguientes:

car::vif(mod.cakes)

##       X1       X2  I(X1^2)  I(X2^2)    X1:X2 
## 3778.083 5921.833 1328.089 5309.339 3063.500

Aquí vemos que los VIF presentan valores muy altos, producto de ajustar un modelo cuadrático. Ahora consideremos el modelo con las covariables centradas:

cakes$X1c = cakes$X1 - mean(cakes$X1)
cakes$X2c = cakes$X2 - mean(cakes$X2)
modc.cakes = lm(Y ~ X1c*X2c + I(X1c^2)+I(X2c^2),data=cakes)
summary(modc.cakes)

## 
## Call:
## lm(formula = Y ~ X1c * X2c + I(X1c^2) + I(X2c^2), data = cakes)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.4912 -0.3080  0.0200  0.2658  0.5454 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  8.070000   0.175044  46.103 5.41e-11 ***
## X1c          0.367558   0.075796   4.849 0.001273 ** 
## X2c          0.096392   0.015159   6.359 0.000219 ***
## I(X1c^2)    -0.156875   0.039446  -3.977 0.004079 ** 
## I(X2c^2)    -0.011950   0.001578  -7.574 6.46e-05 ***
## X1c:X2c     -0.041625   0.010719  -3.883 0.004654 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4288 on 8 degrees of freedom
## Multiple R-squared:  0.9487, Adjusted R-squared:  0.9167 
## F-statistic:  29.6 on 5 and 8 DF,  p-value: 5.864e-05

Los VIFs del modelo con las covariables centradas son:

car::vif(modc.cakes)

##      X1c      X2c I(X1c^2) I(X2c^2)  X1c:X2c 
## 1.000000 1.000000 1.005952 1.005952 1.000000

En este caso, los VIF decrecieron considerablemente con respecto al modelo con las covariables originales.

En la figura 2.8 podemos observar el valor esperado estimado de la palatabilidad para diferentes valores de tiempo y temperatura de horneado.

par(mfrow=c(1,2))
X01.1 = data.frame(X1c = seq(32,38,length.out = 100)-mean(cakes$X1),
                   X2c = 360 - mean(cakes$X2))
X01.2 = data.frame(X1c = seq(32,38,length.out = 100)-mean(cakes$X1),
                   X2c = 350 - mean(cakes$X2))
predX1.1 = predict(modc.cakes,X01.1)
predX1.2 = predict(modc.cakes,X01.2)

X02.1 = data.frame(X1c = 33-mean(cakes$X1),
                   X2c = seq(330,365,length.out = 100) - mean(cakes$X2))
X02.2 = data.frame(X1c = 35-mean(cakes$X1),
                   X2c = seq(330,365,length.out = 100) - mean(cakes$X2))
predX2.1 = predict(modc.cakes,X02.1)
predX2.2 = predict(modc.cakes,X02.2)


plot(X01.1$X1c+mean(cakes$X1),predX1.2,type='l',lwd=2,ylab='palatabilidad',
     xlab='tiempo de horneado (minutos)')
lines(X01.2$X1c+mean(cakes$X1),predX1.1,col=2,lwd=2)
legend('bottomright',c('X2=350','X2=360'),col=1:2,lty=1)
plot(X02.1$X2c+mean(cakes$X2),predX2.2,type='l',lwd=2,ylab='palatabilidad',
     xlab='temperatura de horneado (Fahrenheit)')
lines(X02.2$X2c+mean(cakes$X2),predX2.1,col=2,lwd=2)
legend('bottomright',c('X1=35','X1=33'),col=1:2,lty=1)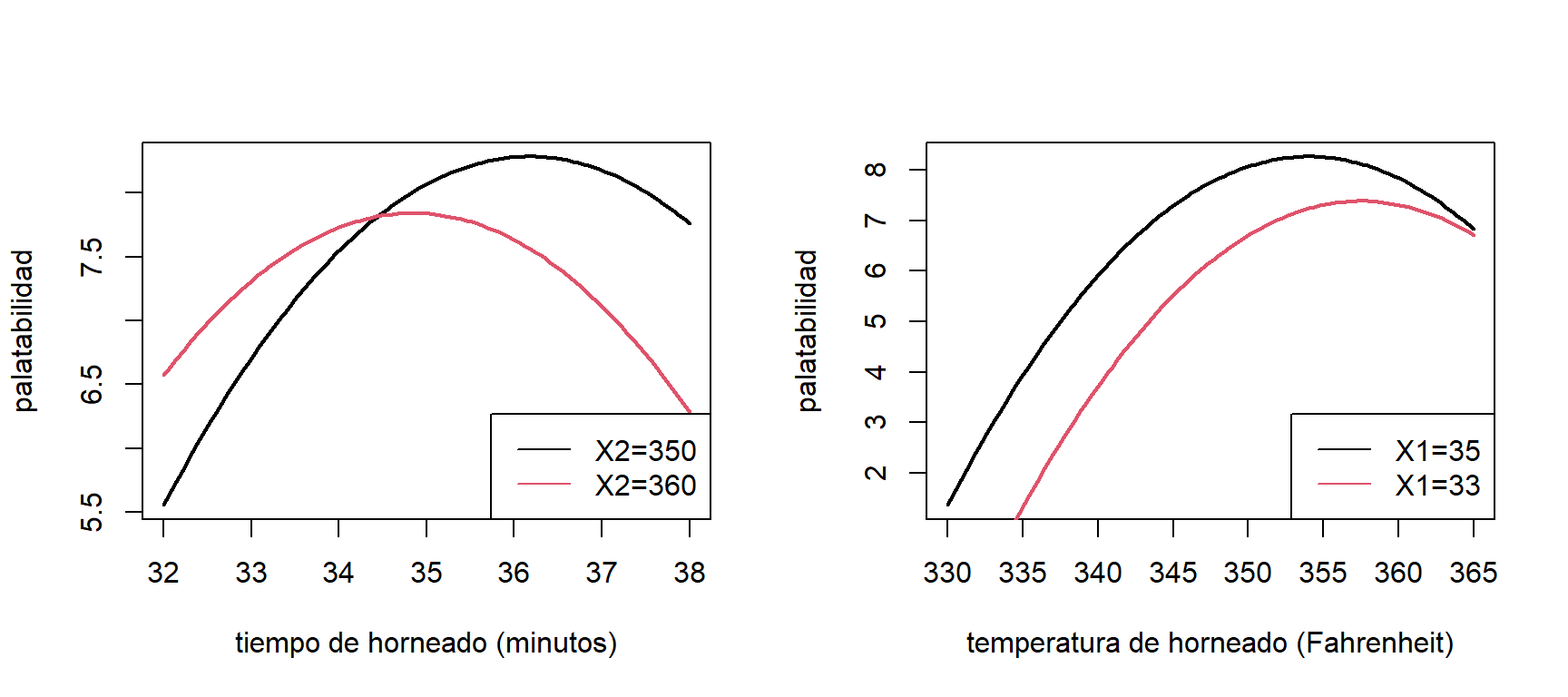

Figure 2.8: Datos de pasteles. Valor esperado de la palatabilidad para diferentes valores de tiempo y temperatura de horneado.

En la Figura 2.8 (izquierda) vemos que, cuando la temperatura es de 350 grados Fahrenheit, el máximo de palatabilidad que se obtiene en un tiempo entre 36 y 37 minutos. Sin embargo, cuando la temperatura se incrementa a 360, la máxima palatibilidad que se puede lograr es menor. Además, se obtiene en un tiempo también menor. El efecto de la interacción también se puede observar en la Figura 2.9 (derecha), pero ahora fijando el tiempo de horneado y variando la temperatura. El gráfico de contornos (Figura 2.9) muestra que la máxima palatabilidad se observa cuando la temperatura está alrededor de 355 y el tiempo de horneado está entre 35 y 36 minutos.

X1 = seq(32, 38, length.out = 50)
X2 = seq(335, 365, length= 50)

y <- outer(X= X1, Y = X2, FUN = function(x, y) {
    predict(modc.cakes, newdata = data.frame(X1c = x-mean(cakes$X1), X2c = y-mean(cakes$X2)))
})

contour(X1, X2, y,xlab='tiempo de horneado (minutos)',
        ylab='temperatura de horneado (Fahrenheit)')

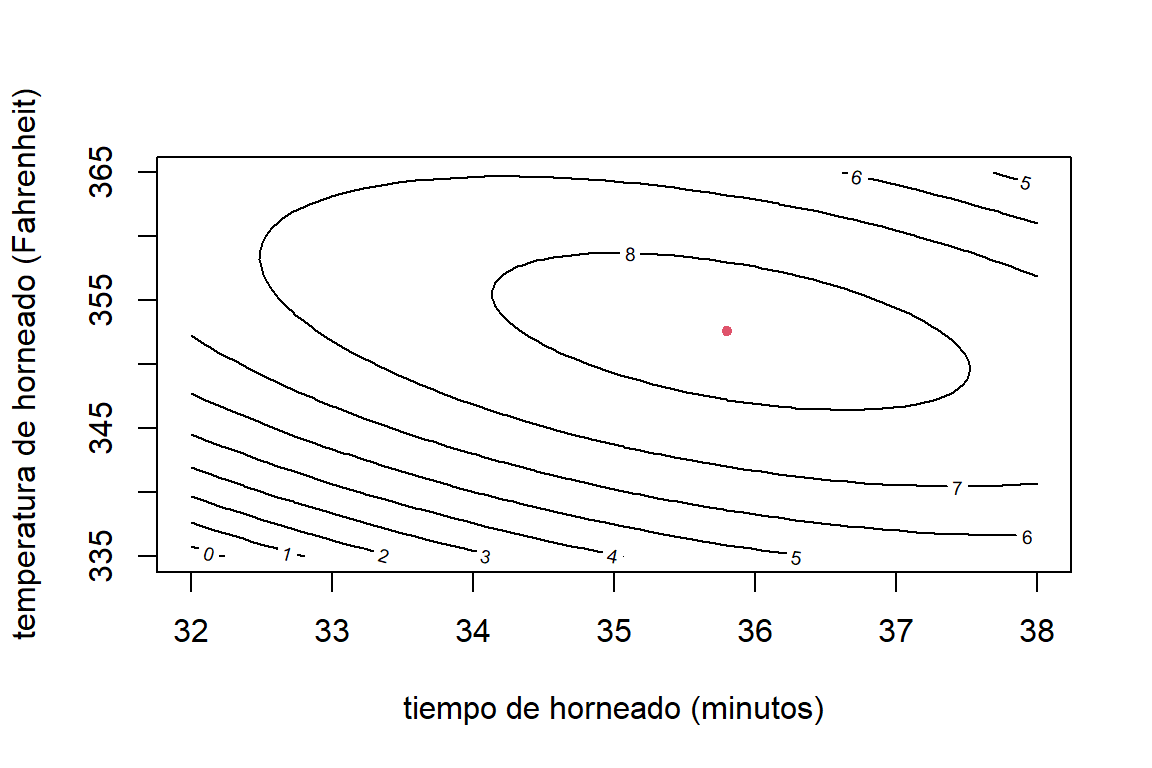
Figure 2.9: Datos de pasteles. Gráfica de contornos.

Para determinar en que combinación de tiempo (X1) y temperatura de horneado (X2) se obtiene la máxima palatabilidad, debemos resolver la siguiente ecuación: \[ \frac{\partial E(Y)}{\partial \boldsymbol x} = \frac{\partial}{\partial \boldsymbol x} \left( \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \beta_{3}x_{1}^2 + \beta_{4}x_{2}^{2} + \beta_{5}x_{1}x_{2} \right) = \boldsymbol 0, \] verificando que se obtiene un máximo. Resolviendo la ecuación anterior, el máximo valor esperado de palatabilidad \((8.3)\) se obtiene en un tiempo de horneado de 35.8 minutos y a una temperatura de F. El intervalo del 95% de confianza en este punto es: \((7.9, 8.7)\).

2.2.3 Datos de Boston

Para los datos de contaminación se puede proponer el siguiente modelo: \[ \mbox{NOx}_{i}^{-1.5} = \beta_{0} + \beta_{1}\mbox{dis}_{i} + \beta_{2}\mbox{dis}_{i}^{2} + \beta_{3}\mbox{dis}_{i}^{3} + \varepsilon_{i}. \] La potencia en la variable respuesta se seleccionó usando el método de Box-Cox. El ajuste del modelo es el siguiente:

Boston$disc = Boston$dis - mean(Boston$dis)
mod3.Boston = lm(I(nox)^(-1.5)~disc+I(disc^2)+I(disc^3),data=Boston)
summary(mod3.Boston)

## 
## Call:
## lm(formula = I(nox)^(-1.5) ~ disc + I(disc^2) + I(disc^3), data = Boston)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.86825 -0.21380  0.00826  0.26905  0.68913 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  2.7939644  0.0244485 114.279  < 2e-16 ***
## disc         0.3675414  0.0104022  35.333  < 2e-16 ***
## I(disc^2)   -0.0461689  0.0059438  -7.768 4.54e-14 ***
## I(disc^3)    0.0020017  0.0009723   2.059     0.04 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3494 on 502 degrees of freedom
## Multiple R-squared:  0.7826, Adjusted R-squared:  0.7813 
## F-statistic: 602.4 on 3 and 502 DF,  p-value: < 2.2e-16

La Figura 2.10 muestra el ajuste del modelo cúbico. Para hacer comparaciones, se muestra también el ajuste lineal y cuadrático. Se observa que el modelo cúbico presenta un buen ajuste. El modelo explica alrededor del \(78.3\)% de la variabilidad de la concentración anual de óxido de nitrógeno. Con el modelo cuadrático, el coeficiente de determinación es de \(0.781\). Sin embargo, se puede observar que este ajuste presenta deficiencias cuando las distancias son muy grandes (mayores a 11).

Datos de Boston. Valor esperado de la concentración anual de óxido de nitrógeno (en partes por diez millones) en función de las distancias a cinco centros de empleo (media ponderada). Modelo lineal (negro), cuadrático (rojo) y cúbico (verde).

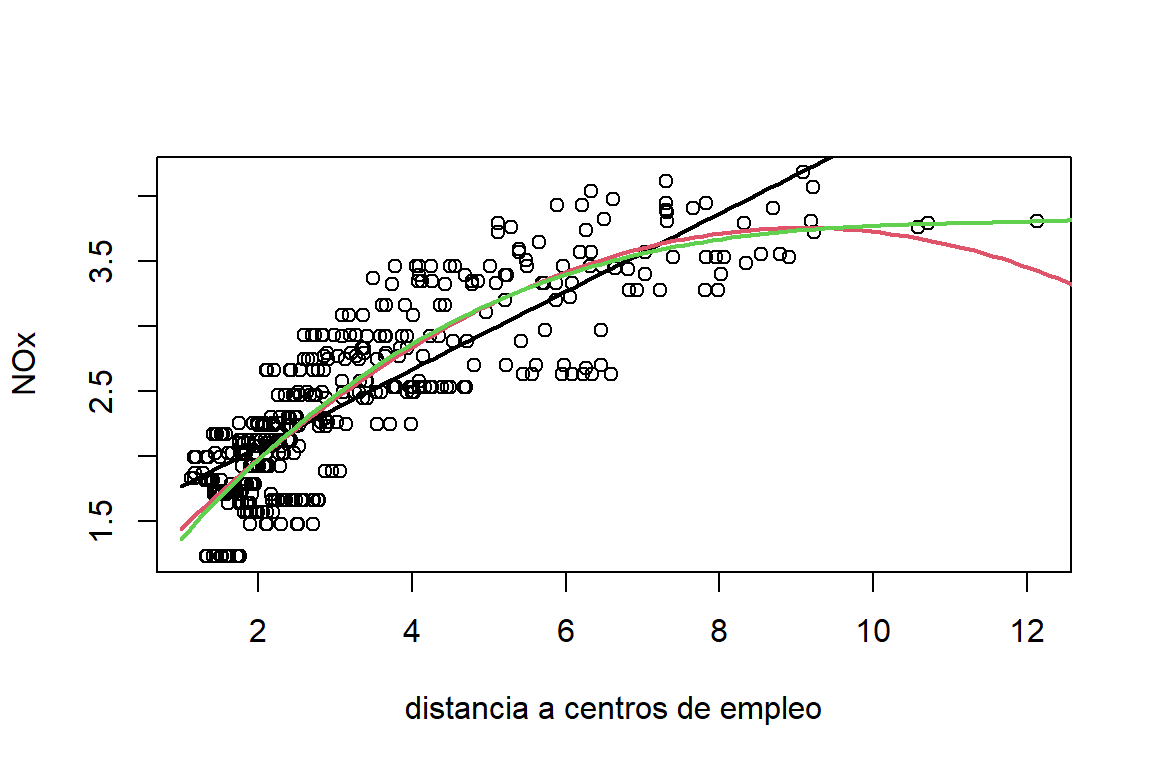
Figure 2.10: Datos de Boston. Valor esperado de la concentración anual de óxido de nitrógeno (en partes por diez millones) en función de las distancias a cinco centros de empleo (media ponderada). Modelo lineal (negro), cuadrático (rojo) y cúbico (verde).

2.3 Regresión por segmentos

El modelo por segmentos se puede expresar como: \[ y_{i} = \beta_{0} + \beta_{1}x_{i} + \beta_{2}(x_{i}-t)^{0}_{+} + \beta_{3}(x_{i}-t)^{1}_{+} + \varepsilon_{i}. \] donde: \[ (x_{i}-t)_{+}^{r} = \begin{cases} 0 & \mbox{ si } x_{i} + t \leq 0, \\ (x_{i}-t)^{r} & \mbox{ si } x_{i} + t > 0. \\ \end{cases} \nonumber \] Por lo tanto, si \(x_{i} \leq t\), \(E(y_{i}| x_{i}) = \beta_{0} + \beta_{1}x_{i}\). Mientras que, si \(x_{i} > t\), tenemos que \(E(y_{i}| x_{i}) = (\beta_{0} + \beta_{2} - \beta_{1}t) + (\beta_{1} + \beta_{3})x_{i}\).

Este modelo está representado graficamente en la Figura 2.11. Cuando \(\beta_2 \neq 0\), el modelo presenta una discontinuidad en \(t\). Mientras que, cuando se fija \(\beta_2 = 0\), el modelo presenta un cambio de pendiente en el punto \(t\). Además, \(\beta_3\) indica el cambio de pendiente.

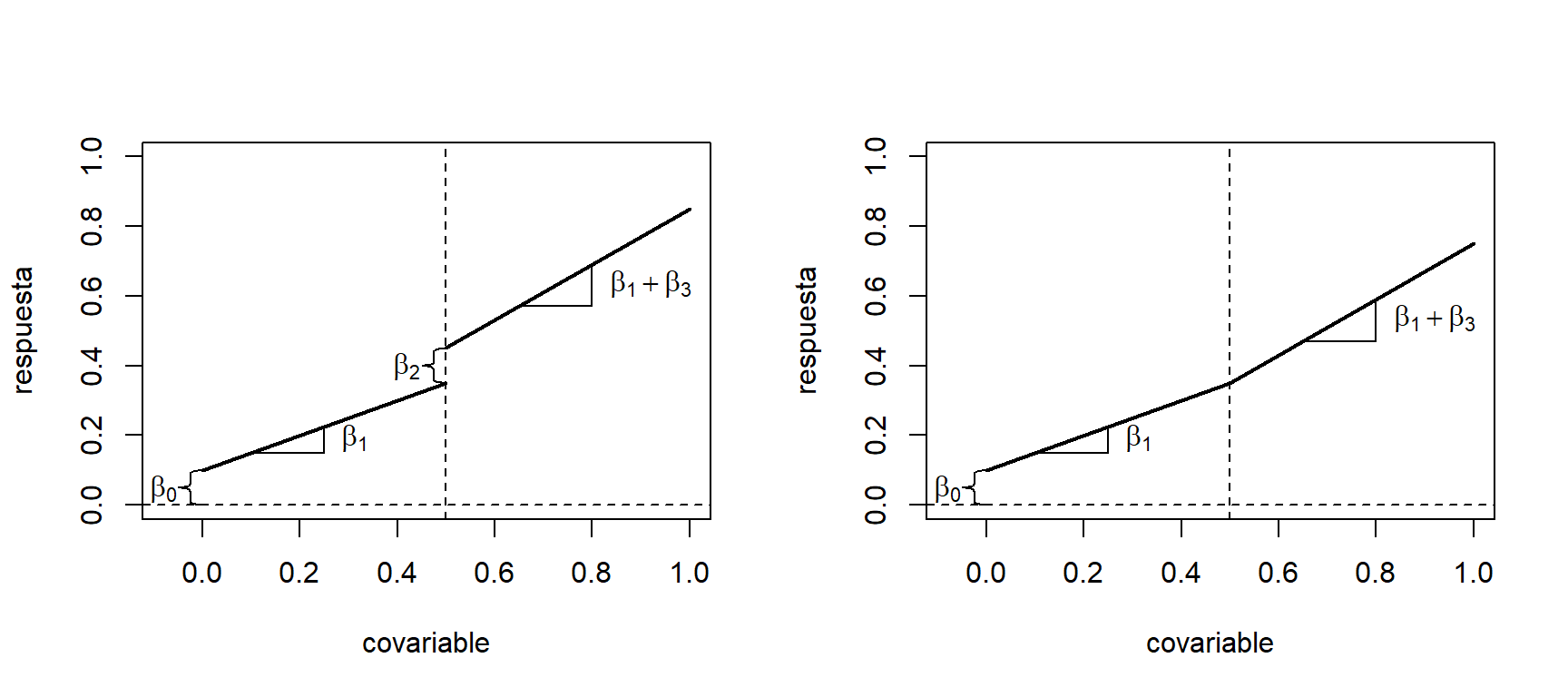
Figure 2.11: Modelo de regresión por segmentos. Modelo con discontinuidad en \(t\) (izquierda). Modelo con cambio de pendiente en \(t\) (derecha).

Aquí asumimos que \(t\) es conocido. Si este valor se asume como desconocido, debe estimarse a partir de los datos como un parámetro adicional. Sin embargo, se tendría que recurrir a un método de estimación para modelos no-lineales.

2.3.1 Ejemplo

library(MPV)
data(p7.11)
plot(p7.11,ylab='costo de producción por unidad (USD)',xlab='Unidades por lote')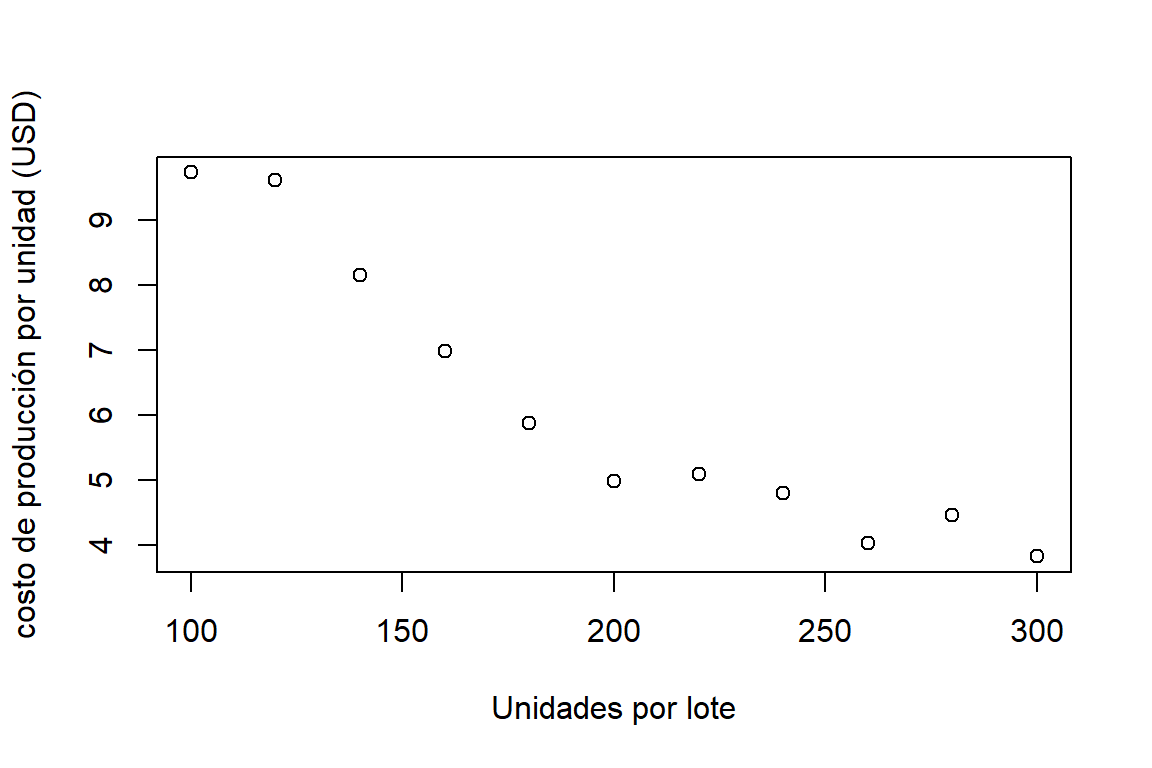

Figure 2.12: Datos de costos por lote. Diagram de dispersión de el costo de producción promedio por unidad (USD) y el tamaño del lote (unidades).

Considere la base de datos p7.11 de la librería MPV. Aquí se quiere modelar la relación entre el costo de producción promedio por unidad (USD) y el tamaño del lote (unidades). Este relación se puede observar en la Figura 2.12. Se puede observar que la relación entre las variables es lineal. Sin embargo, se aprecia un posible cambio de pendiente en el punto \(x=200\). Por esta razón se propone el siguiente modelo: \[ y_{i} = \beta_{0} + \beta_{1}x_{i} + \beta_{2}(x_{i}-200)_{+}^{1} + \varepsilon_{i}. \] Note que no se asume ninguna discontinuidad. El ajuste del modelo es:

p7.11$x2 = p7.11$x - 200
p7.11$x2[p7.11$x < 200] = 0
mod.lotes = lm(y~.,data=p7.11)
summary(mod.lotes)

## 
## Call:
## lm(formula = y ~ ., data = p7.11)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.37596 -0.16641 -0.09677  0.20363  0.51734 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 15.116481   0.535383  28.235 2.67e-09 ***
## x           -0.050199   0.003332 -15.065 3.73e-07 ***
## x2           0.038852   0.005946   6.534 0.000181 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3157 on 8 degrees of freedom
## Multiple R-squared:  0.9829, Adjusted R-squared:  0.9787 
## F-statistic: 230.4 on 2 and 8 DF,  p-value: 8.474e-08

A partir del ajuste podemos concluir que, por cada unidad que incrementa el lote, el costo de producción disminuye en \(0.05\)USD. Si embargo, si el tamaño del lote es mayor a \(200\), el costo de producción disminuye solamente \(0.01\)USD cuando el lote aumenta en un artículo. Gráficamente, el ajuste se puede observar en la Figura 2.13.

b.lotes = mod.lotes$coefficients
plot(p7.11$x,p7.11$y,ylab='costo de producción por unidad (USD)',xlab='unidades por lote')
x = c(100,200)
lines(x,b.lotes[1]+x*b.lotes[2],lwd=2)
x = c(200,300)
lines(x,b.lotes[1]-200*b.lotes[3]+x*(b.lotes[2]+b.lotes[3]),lwd=2)
abline(v=200,lty=2)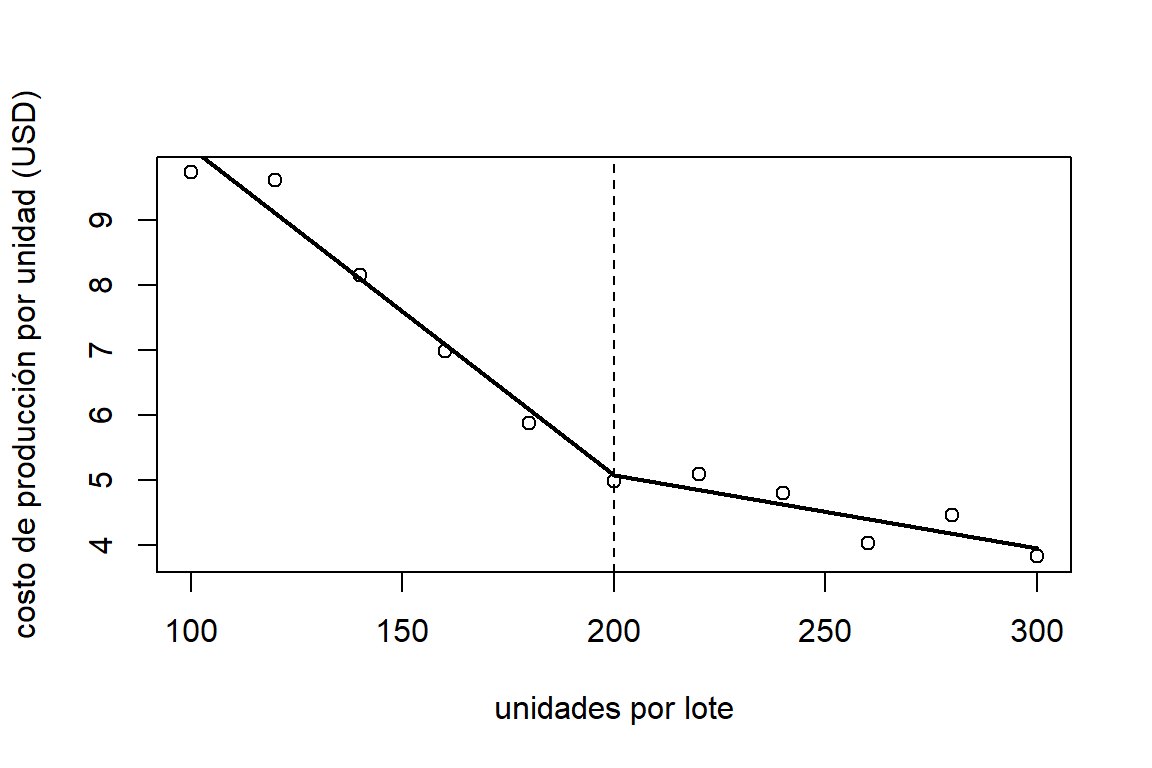

Figure 2.13: Datos de costos por lote. Diagram de dispersión de el costo de producción promedio por unidad (USD) y el tamaño del lote (unidades).