Capítulo 7 Modelo logístico
7.1 Casos de estudio
7.1.1 Mortalidad de escarabajos
Vamos a continuar con los datos del estudio sobre los escarabajos del capítulo anterior.
7.1.2 Bajo peso al nacer
Con los datos de la librería , se quiere indentificar factores de riesgo asociados con el nacimiento de niños con bajo peso (es decir, un peso al nacer menor de \(2.5\)kgs). Se tiene información de 189 recién nacidos y sus madres atendidos en una hospital (Baystate Medical Center, Springfield, Mass en 1986). Los posibles factores que pueden afectar el bajo al peso son:
age: edad de la madre (años),lwt: peso de la madre antes del embarazo (libras),smoke: estado de tabaquismo durante el embarazo (0 no, 1 si),ptl: historia de parto prematuro (número de casos).
La variable de respuesta es si el bebé nace con bajo peso (1 si peso \(<\) 2.5 kgs, 0 si peso \(\geq\) 2.5 kgs, low).
Para este caso, se puede ajustar modelo logístico. Sea \(y_i=1\) si el \(i\)-ésimo bebé nace con bajo peso, \(y_i=0\) si lo contrario. Por lo que la densidad de \(y_i\) está definida como: \[ f(y_i;\pi_i)=\pi_i^{y_i}(1-\pi_i)^{(1-y_i)}, \] donde \(\pi_i\) es la probabilidad de que el \(i\)-ésimo bebé nazca con bajo peso. La función de enlace puede definirse como: \[ \log\begin{pmatrix} \frac{\pi_i}{1-\pi_i} \end{pmatrix}=\beta_0+\beta_1\text{age}_i+\beta_2\text{lwt}_i+\beta_3\text{smoke}_i+\beta_4\text{ptl}_i. \] Sin embargo, se puede considerar alguna función de enlace diferente, como veremos adelante.
7.1.3 Estudio de teratología
Los datos de la librería son de un estudio para investigar los efectos de unos régimenes alimenticio en el desarrollo fetal de ratas. En este experimento, 58 ratas hembras con dietas deficientes en hierro se dividieron en cuatro grupos. Tres grupos recibieron inyecciones semanales de suplementos de hierro, a diferentes dosis, para normalizar sus niveles de hierro. Mientras que, el grupo restante no recibieron ningún suplemento (placebo). Luego, las ratas fueron preñadas, sacrificadas luego de 3 semanas, y se contó el número de fetos muertos en cada camada.
En la Figura 7.1 se puede observar la relación entre el número de fetos muertos por tratamiento, y también, la relación con los niveles de hemoglobina de las ratas hembras.
data(lirat,package = 'VGAM')
par(mfrow=c(1,2))
#Proporcion de fetos muestos vs tratamiento
plot(lirat$grp,lirat$R/lirat$N,xlab="Tratamiento",ylab="Proporción de fetos muertos")
#Proporcion de fetos muestos vs Hemoglobina
plot(lirat$hb,lirat$R/lirat$N,xlab="Hemoglobina",ylab="Proporción de fetos muertos")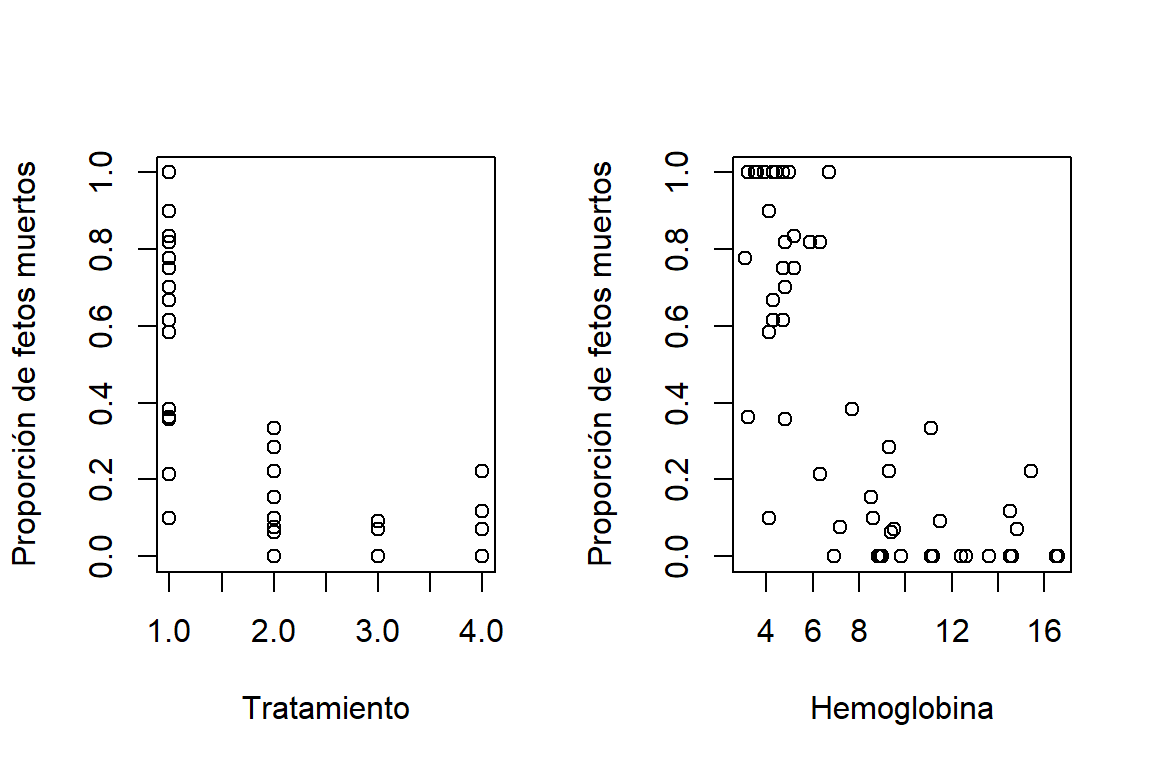
Figure 7.1: Datos de teratoligía. Relación entre la proporción de fetos muertos por camada con los tratamientos (izquierda) y los niveles de hemoglobina de la madra (derecha)
Si consideramos:
\[
y_{ij} = \begin{cases}
1 & \mbox{ si el feto } j \mbox{ de la camada }i\mbox{ está muerto}, \\
0 & \mbox{ si lo contrario}, \\
\end{cases}
\]
la variable número de fetos muertos se puede asociar a una distribución binomial:
\[
y_i = \sum_{j=1}^{n_i} y_{ij} \sim \mbox{binomial}(n_i, \pi_i),
\]
donde \(n_i\) es el tamaño de la camada y \(\pi_i\) es la probabilidad de que el feto muera. Dado que \(\pi_i\) depende del tratamiento y de los niveles de hemoglobina de la rata hembra, se propone que:
\[
\log\begin{pmatrix} \frac{\pi_i}{1-\pi_i} \end{pmatrix}=\beta_0+\beta_1\text{grp1}_{i}+\beta_2\text{grp2}_{i}+\beta_3\text{grp3}_{i}+\beta_4\text{hb}_i,
\]
donde: \(\text{grp1}_{i}=1\) si la \(i\)-ésima hembra pertenece al grupo 1, \(\text{grp1}_{i}=0\) si lo contrario; \(\text{grp2}_{i}=1\) si la \(i\)-ésima hembra pertenece al grupo 2, \(\text{grp2}_{i}=0\) si lo contrario; \(\text{grp3}_{i}=1\) si la \(i\)-ésima hembra pertenece al grupo 3, \(\text{grp3}_{i}=0\) si lo contrario; y hb_i es el nivel de hemoglobina de la hembra \(i\).
7.2 Datos agrupados o datos no agrupados
Los datos binarios tienen dos tipos de formatos:
Datos agrupados: Hay \(n_i\) observaciones que tienen los mismos valores de las covariables \(x_i\). Aquí tenemos que para agrupación, \(y_i \sim\)binomial\((n_i,\pi_i)\).
Datos no agrupados: Hay \(n_i=1\) (o muy pocas) observaciones por cada \(x_i\). Es decir que, cada \(y_i\) sigue una distribución Bernoulli\((\pi_i)\).
Las propiedades asintóticas de las inferencias para los datos no agrupados aplican cuando \(N \to \infty\). Mientras que para datos agrupados, aplican cuando \(\sum_{i=1}^nn_i\to\infty\).
7.2.1 Datos agrupados
Para datos agrupados, \(D\) y \(X^2\) sirven para evaluar si el ajuste del modelo es bueno o no. Aquí podemos plantear las siguientes hipótesis: \(H_0\) indica que el modelo se ajusta bien a los datos, \(H_1\) lo contrario.
Si \(H_0\) es cierta (y \(\sum_{i=1}^nn_i\to\infty\)), entonces \(D\) y \(X^2\) siguen una distribución \(\chi^2\) con \((n-p)\) grados de libertad.
7.2.2 Datos no agrupados
Las distribuciones límite para \(D\) y \(X^2\) no aplican para datos no agrupados. Tampoco para datos agrupados con \(N\) grande y algunos \(n_i\) muy pequeños. Se puede aproximar \(D\) y \(X^2\) agrupando \((\boldsymbol x_i,\hat{\boldsymbol y})\) por particiones del espacio de covariables o por particiones de \(\hat{\pi}\). En estos casos, es preferible evaluar la falta de ajuste comparando el modelo propuesto contra modelos más generales.
7.3 Funciones de enlace
En los modelos anteriores hemos propuesto funciones de enlace logit: \(log\begin{pmatrix} \frac{\pi_i}{1-\pi_i} \end{pmatrix}=\boldsymbol x_i'\boldsymbol \beta\).Lo que implica que:
\[ \pi_i=g^{-1}(\boldsymbol x_i'\boldsymbol \beta)=\frac{\exp(\boldsymbol x_i'\boldsymbol \beta)}{1+\exp(\boldsymbol x_i'\boldsymbol \beta)}=\frac{1}{1+\exp(-\boldsymbol x_i'\boldsymbol \beta)} \] Sin embargo, podemos utilizar otras funciones de enlace. Por ejemplo, la función Probit: \[ \Phi^{-1}(\pi_i)=\boldsymbol x'_i\boldsymbol \beta\quad \pi_i=\Phi(\boldsymbol x'_i\boldsymbol \beta), \] donde \(\Phi(\cdot)\) es función acumulativa de la distribución normal estándar. La función Log-log complementaria: \[ \pi_i=1-\exp[-\exp(\boldsymbol x'_i\boldsymbol \beta)] \quad \log[-\log(1-\pi_i)]=\boldsymbol x'_i\boldsymbol \beta. \] En la Figura 7.2 podemos observar la estimación de la probabilidad de que el escarabajo muera utilizando diferentes funciones de enlace (logit, probit, log-log complementaria). Graficamente, la función log-log complementaria parece mostrar mejores estimaciones que las otras.
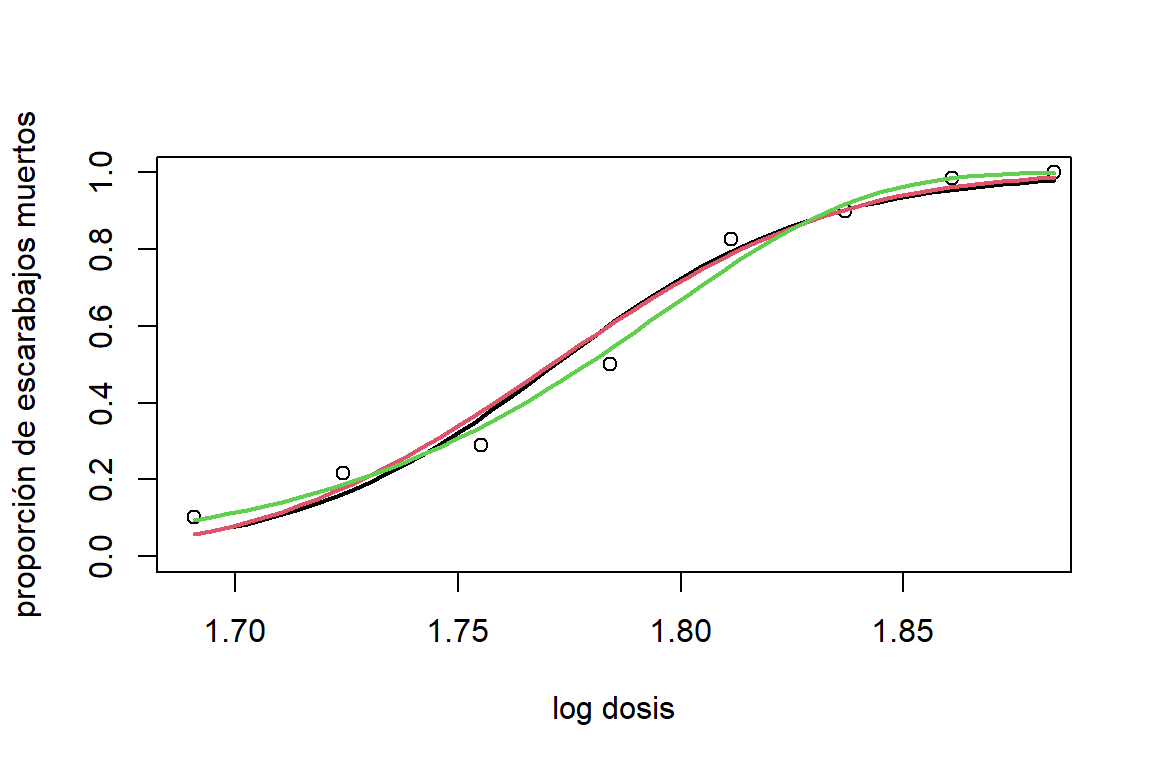
Figure 7.2: Datos de mortalidad de escarabajos. Estimaciones de la probabilidad de que el escarabajo muera en función del logaritmo de la dosis de disulfuro de carbono gaseoso utilizando diferentes funciones de enlace: logit(negro), probit(rojo) y cloglog(verde).
Este resultado se puede comprobar utilizando criterios de información:
## [1] 41.43027## [1] 40.3178## [1] 33.644487.4 Curva característica operativa del receptor(ROC)
Para evaluar el poder predictivo del modelo se puede construir una tabla de contingencia comparando \(y_i\) con la predicción \(\widehat{y}_i\) a través del modelo. Para datos no agrupados, la predicción \(\widehat{y}_i\) se define como: \[ \widehat{y}_i = \begin{cases} 1 & \mbox{si } \widehat{\pi}_i > \pi_0, \\ 0 & \mbox{si } \widehat{\pi}_i \leq \pi_0, \\ \end{cases} \] para un punto de corte \(\pi_0\) definido por el investigador, por ejemplo \(\pi_0 = 0.5\). Con esto podemos contruir la siguiente tabla:
| \(y=0\) | a | c |
| \(y=1\) | b | d |
donde \(a\) y \(b\) corresponde al conteo de predicciones negativas \((\widehat{y}= 0)\) correctas (cuando \(y=0\)) e incorrectas (cuando \(y=1\)), respectivamente. Mientras que \(c\) y \(d\) son los contenos de predicciones positivas \((\widehat{y}= 1)\) incorrectas (cuando \(y=0\)) y correctas (cuando \(y=1\)), respectivamente.
El recuento de casillas en esta tabla permite estimar la sensibilidad, definida como la probabilidad de identificar correctamente un caso positivo, esto es: \[ P(\widehat{y}=1|y=1) = \frac{d}{b+d}, \] y la especificidad, definida como la probabilidad de identificar correctamente un caso negativo, \[ P(\widehat{y}=0|y=0) = \frac{a}{a+c}. \] Si el objetivo del modelo es realizar predicciones es preferible obtener valores altos para estas métricas. Sin embargo, estos valores dependen de \(\pi_0\).
Consideremos los datos de peso al nacer. Se propone el siguiente modelo para la probabilidad de nacer con bajo peso: \[ \mbox{logit } \pi_i = \beta_0+ \mbox{age}_i\beta_1+ \mbox{lwt}_i\beta_2 + \mbox{smoke}_i\beta_3 + \mbox{ptl}_i\beta_4, \] El ajuste del modelo es:
##
## Call:
## glm(formula = low ~ age + lwt + smoke + ptl, family = binomial,
## data = birthwt)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.275961 1.031063 1.238 0.2159
## age -0.048859 0.033796 -1.446 0.1483
## lwt -0.010412 0.006219 -1.674 0.0941 .
## smoke 0.550111 0.334455 1.645 0.1000
## ptl 0.695720 0.336895 2.065 0.0389 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 234.67 on 188 degrees of freedom
## Residual deviance: 218.36 on 184 degrees of freedom
## AIC: 228.36
##
## Number of Fisher Scoring iterations: 4Estos resultados muestran que el estado de tabaquismo y el historial de partos prematuros son factores de riesgo para el bajo peso al nacer. Sin embargo, el primero no tiene un aporte significativo dentro del modelo.
Ahora vamos a evaluar el poder predictivo del modelo. Si definimos \(\pi_0=0.5\), tenemos los siguientes resultados:
| \(y=0\) | 123 | 7 |
| \(y=1\) | 49 | 10 |
Por lo tanto, la sensibilidad es \(10/59 = 0,169\) y la especificidad es \(123/130 = 0.946\). Con este punto de corte, el modelo tiene una predictividad alta para los recién nacidos con peso adecuado (alta especificidad). Sin embargo, la probabilidad de falsos positivos es alta (baja sensibilidad). Ahora, si definimos \(\pi_0= 0,3\) obtenemos lo siguiente:
| \(y=0\) | 79 | 51 |
| \(y=1\) | 19 | 40 |
En este caso la sensibilidad aumentó \((40/59 = 0,678)\), pero la especificidad disminuye \((79/130 = 0,607)\).
Dado que la sensibilidad y especificidad tiene una alta dependencia del punto de corte, lo preferible es calcular estas cantidades para muchos valores de \(\pi_0\) y buscar un valor ‘óptimo’. En la Figura 7.3 podemos observar que a medida que aumenta \(\pi_0\) la sensibilidad disminuye y la especificidad aumenta.
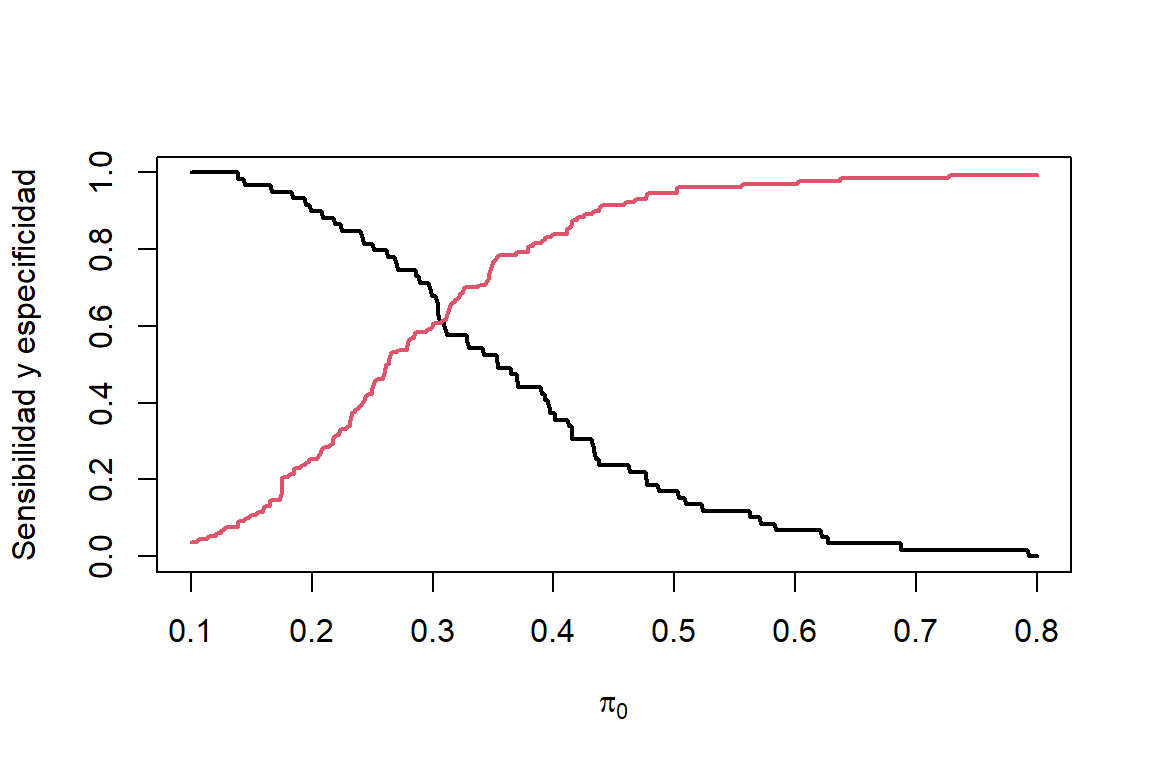
Figure 7.3: Datos de bajo peso al nacer. Sensibilidad (linea negra) y especificidad (linea roja) para diferentes puntos de corte.
La sensibilidad es la tasa de verdaderos positivos (tvp), mientras que, el complemento de la especificidad \((P(\widehat{y}= 1 | y=0))\) es la tasa de falsos positivos (tfp). El gráfico de la tasa de verdaderos positivos en función de la tasa de falsos positivos para diferentes valores de \(\pi_0\), entre \(0\) y \(1\), lleva el nombre de curva característica operativa del receptor (ROC). Cuando \(\pi_0\) es muy cercano a \(1\), casi todas las predicciones son \(\widehat{y}=0\); entonces tenemos (tvp,tfp)\(\approx(0,0)\). Mientras que, cuando \(\pi_0\) es muy cercano a \(0\), casi todas las predicciones son \(\widehat{y}=1\); entonces tenemos (tvp,tfp)\(\approx(1,1)\). esto lo podemos ver en la Figura 7.4.
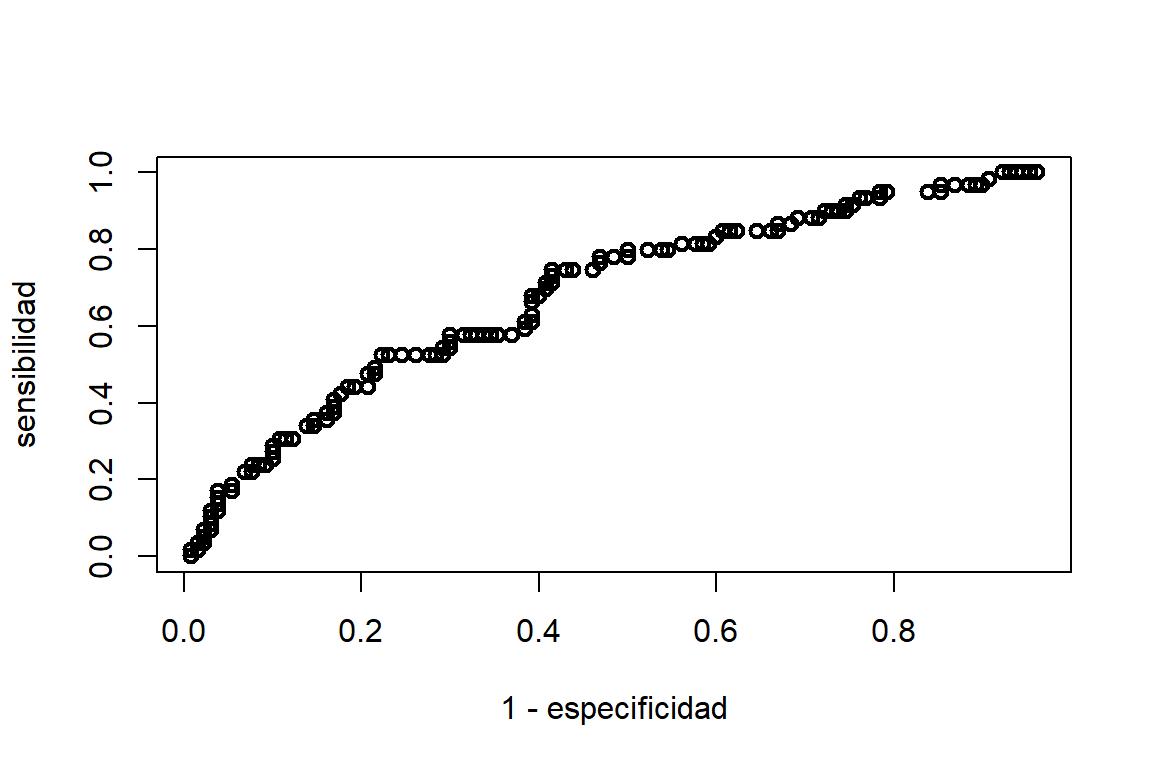
Figure 7.4: Datos de bajo peso al nacer. Sensibilidad (linea negra) y especificidad (linea roja) para diferentes puntos de corte.
Si el modelo realiza buenas predicciones, para un valor de especificidad dado, se espera que la sensibilidad también sea alta. Por lo tanto, el poder predictivo del modelo se puede medir a través del área bajo la curva del gráfico ROC. Esta medida es llamada índice de concordancia.
En R, las curvas ROC se puede realizar por medio de la función roc de la librería pROC de la siguiente forma:
library(pROC)
modbw.logit = glm(low~age+lwt+ptl+smoke,family=binomial(logit),data=birthwt)
modbw.probit = glm(low~age+lwt+smoke+ptl,family=binomial(probit),data=birthwt)
ROCbw.logit = roc(birthwt$low~modbw.logit$fitted.values)## Setting levels: control = 0, case = 1## Setting direction: controls < cases## Setting levels: control = 0, case = 1
## Setting direction: controls < cases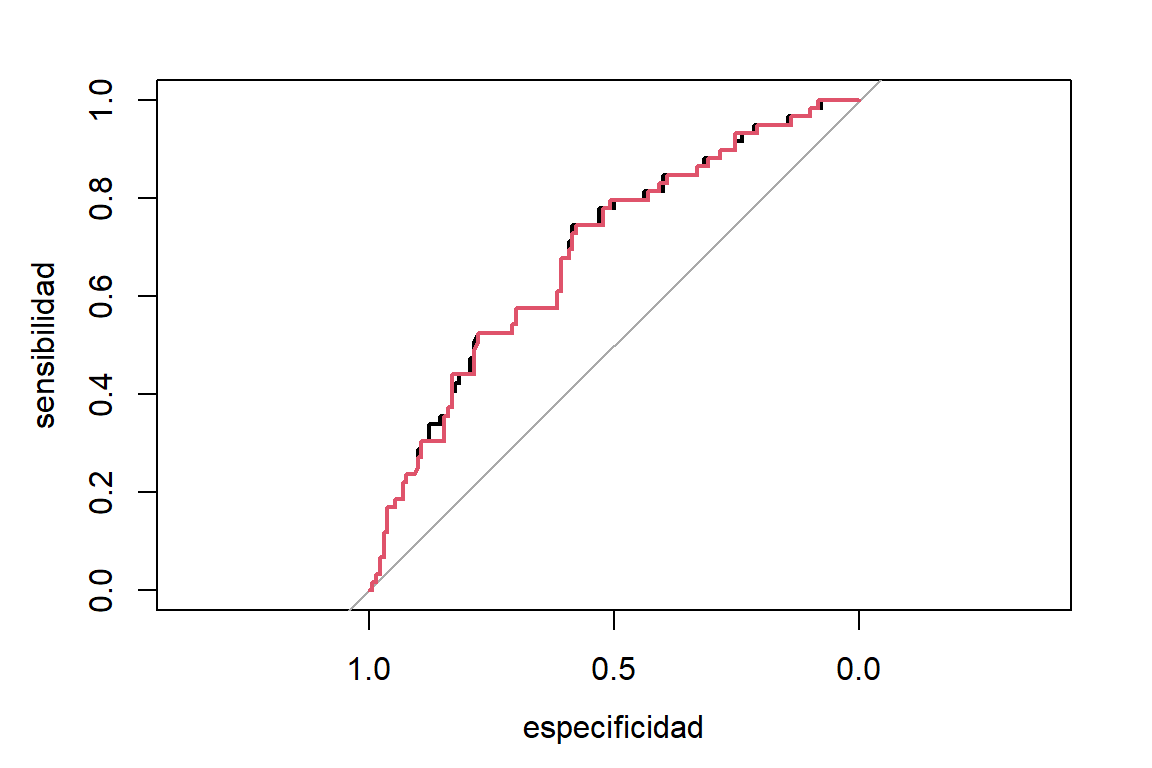
Figure 7.5: Datos de bajo peso al nacer. Curva ROC para predecir bajo peso al nacer usando el modelo logístico (negro) y el probit (rojo)
En la Figura 7.5 se puede observar que ambas funciones de enlace proporcionan el mismo poder predictivo. El índice de concordancia es de \(AUC= 0,6884\) para el modelo logístico y \(AUC= 0,6866\) para el modelo probit.
Para datos agrupados, la base de datos se debe desagrupar para obtener la curva ROC. Por ejemplo para los datos de escarabajos:
obs.morir = unlist(apply(Datos.esc,1,function(x){rep(c(1,0),c(x[3],x[2]-x[3]))}))
prob.morir =rep(modEsc.logit$fitted.values,Datos.esc$n)
ROCesc = roc(obs.morir~prob.morir)## Setting levels: control = 0, case = 1## Setting direction: controls < cases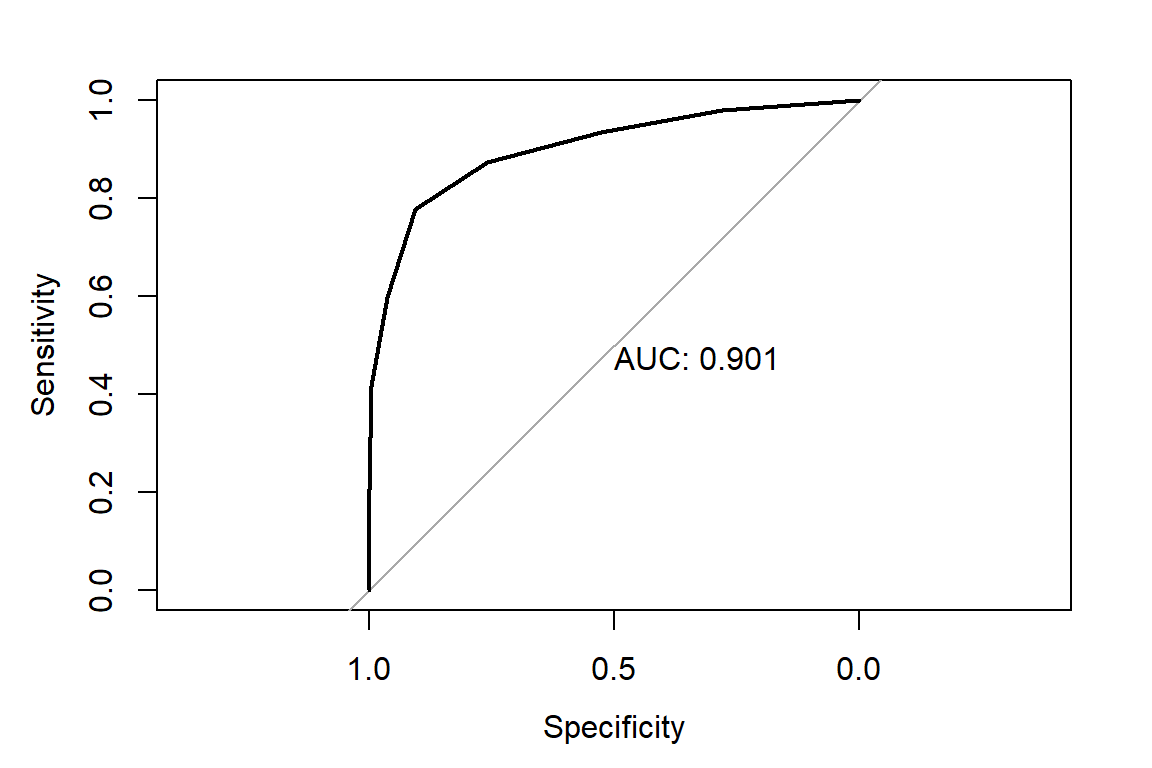
Figure 7.6: Datos de mortalidad de escarabajos. Curva ROC para el modelo logístico
7.5 Sobredispersión
En un experimento Bernoulli se asume que los \(n_i\) ensayos para la observación \(i,\quad (y_{i1},...y_{in_i})\), son independientes. Por lo tanto, para \(y_i = \sum_{j=1}^{n_i}y_{ij}/n_i\),tenemos que:
\[ E(y_i)=\pi_i \quad \text{y} \quad V(y_i)=\pi_i(1-\pi_i)\frac{1}{n_i}. \]
Pero, hay casos donde las observaciones \((y_{i1},...y_{in_i})\) están correlacionadas, lo que hace que \(V(y_{i}) \neq V(y_i)=\pi_i(1-\pi_i)\frac{1}{n_i}\). Si asumimos que \(cor(y_{is},y_{it})=\phi\), para todo \(s\ne t\), tenemos que:
\[ V(y_{it})=\pi_i(1-\pi_i)\quad \text{y} \quad cov(y_{it},y_{is})=\phi\pi_i(1-\pi_i). \]
En este caso, la varianza de \(y_i\) es:
\[ V(y_i)=V\begin{pmatrix} \sum_{j=1}^{n_i}\frac{y_{ij}}{n_i}\end{pmatrix}=\frac{1}{n_i^2} \left[ \sum_{j=1}^{n_i}V(y_{it})+2\sum\sum_{s<t}cov(y_{is},y_{it}) \right]=[1+\phi(n_i-1)]\frac{\pi_i(1-\pi_i)}{n_i}. \] Dependiendo del valor de \(\phi\), la varianza de \(y_i\) puede ser mayor o menor a la esperada bajo una distribución binomial. Si \(\phi_i > 0\), tenemos un problema de sobredispersión (los datos tienen una varianza superior a la que se asume bajo un modelo binomial). Mientras que, si \(-(n_i-1)^{-1}<\phi<0\), hay presencia de subdispersión. El segunda caso es menos frecuenta en datos reales.
7.5.1 Evaluación de sobredispersión
En el caso del modelo binomial, el estadístico de \(\chi^2\) de Pearson está definido como:
\[ X^2=\sum_{i=1}^n\frac{(y_i-\widehat{\pi}_i)^2}{\widehat{\pi}_i(1-\widehat{\pi}_1)/n_i}. \] Si el modelo binomial proporciona buen ajuste, \(X^2\) sigue (asintóticamente) una distribución \(\chi^2\) con \(n-p\) grados de libertad. Por lo tanto, un indicador de posible inflación de varianza es: \[ \widehat{\phi}=\frac{X^2}{n-p}. \] Si hay problemas de sobredispersión, entonces \(\widehat{\phi} > 1\).
7.6 Distribución beta-binomial
El modelo beta-binomial es una alternativa para modelar datos binomial con sobredispersión. Esta distribución parte de una mezcla de una distribución binomial con una distribución beta. Sea \(y^{*}\) el número de éxitos de \(n\) ensayos Bernoulli. Se puede suponer la siguiente distribución de \(y^{*}\): \[ y^{*}|\pi\sim \mbox{binomial}(n,\pi), \mbox{ donde } \pi\sim \mbox{beta}(\alpha_1,\alpha_2). \] La función de densidad de \(\pi\) es: \[ f(\pi;\alpha_1,\alpha_2)=\frac{\Gamma(\alpha_1+\alpha_2)}{\Gamma(\alpha_1)\Gamma(\alpha_2)}\pi^{\alpha_1-1}(1-\pi)^{\alpha_2-1}, \] con \(\alpha_1>0\) y \(\alpha_2>0\). Asumiendo \(\mu=\frac{\alpha_1}{\alpha_1+\alpha_2}\) y \(\theta=1/(\alpha_1+\alpha_2)\), tenemos:
\[ E(\pi)=\mu\quad\text{y}\quad V(\pi)=\mu(1-\mu)\frac{\theta}{1+\theta}. \]
La distribución beta-binomial se obtiene al marginalizar \(y^{*}\). Esto es:
\[ f(y^{*};n,\mu,\theta)=\int f(y^{*}|\pi)f(\pi)d\pi. \] Al resolver la integral anterior, encontramos la función de densidad de la distribución beta-binomial es:
\[ f(y^{*};n,\mu,\theta)=\begin{pmatrix} n \\ y^{*} \end{pmatrix}\frac{\begin{bmatrix} \Pi_{k=0}^{y^{*}-1}(\mu+k\theta)\end{bmatrix} \begin{bmatrix} \Pi_{k=0}^{n-y^{*}-1}(1-\mu+k\theta)\end{bmatrix}}{\begin{bmatrix} \Pi_{k=0}^{n-1}(1+k\theta) \end{bmatrix}}, \]
para \(y^{*}=0,1,...,n.\) El valor esperado y varianza de \(y = \frac{y^{*}}{n}\) son:
\[ E(y)=\mu\quad\text{y}\quad V(y)=\left[ 1+(n-1)\frac{\theta}{1+\theta} \right]\frac{\mu(1-\mu)}{n} = \left[ 1+(n-1)\phi \right]\frac{\mu(1-\mu)}{n}. \]
Por lo cual, \(\phi > 0\) es la correlación entre ensayos Bernoulli. La distribución de probabilidad de la distribución beta-binomial se puede observar en la Figura 7.7. Aquí vemos que la dispersión de la distribución beta-binomial aumenta con el parámetro \(\phi\).
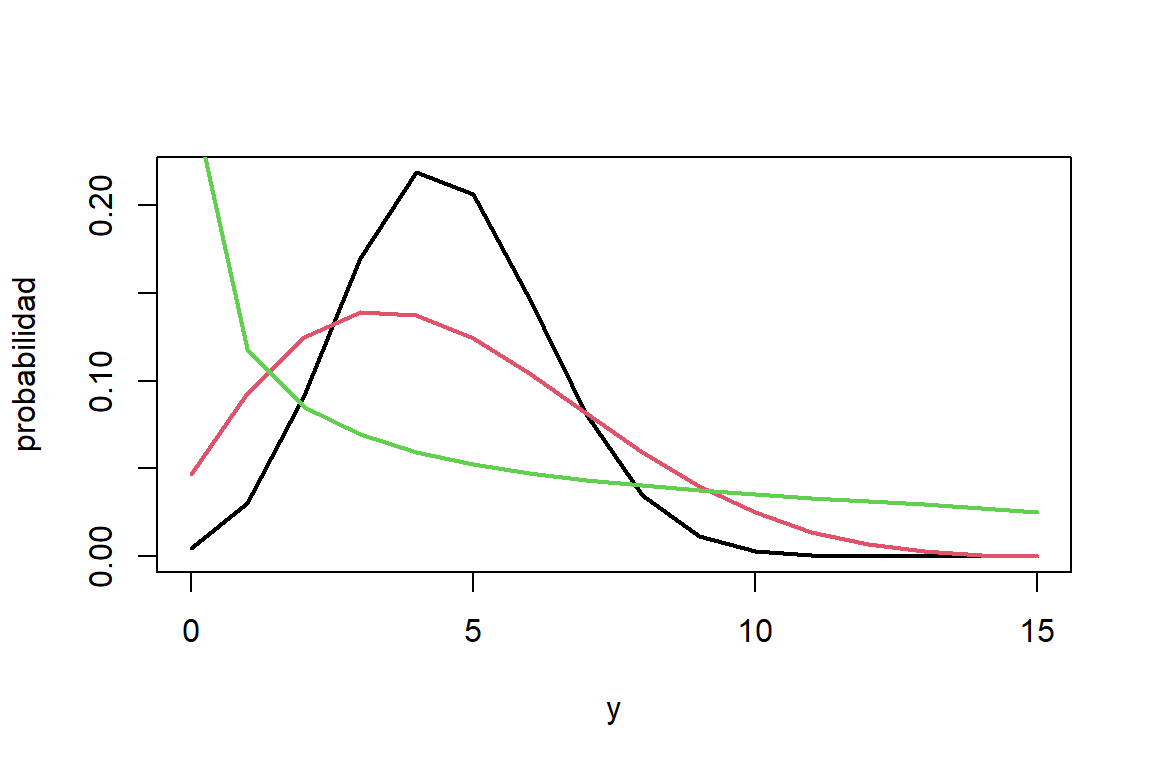
Figure 7.7: Distribución de probabilidad de Binomial(15,0.3) (negro), beta-binomial(15,0.3,0.1) (rojo), beta-binomial(15,0.3,0.4) (verde)
7.6.1 Modelo beta-binomial
El modelo beta-binomial para \(y_i^{*}\) se define como: \[ y_i^{*}|\pi_i\sim \mbox{binomial}(n_i,\pi_i), \mbox{ donde } \pi_i\sim \mbox{beta}(\mu_i,\phi), \] donde \(\mbox{logit } \mu_i = \boldsymbol x_{i}'\boldsymbol \beta\) (si usamos una función de enlace logit). Por lo cuál, para \(y_i = \frac{y_i^{*}}{n_i}\) se tiene que: \[ E(y_i)=\mu_i\quad\text{y}\quad V(y_i)=[1+(n-1)\phi]\mu_i(1-\mu_i)/n_i, \] La estimación de los parámetros \((\beta,\phi)\) se hace por máxima verosimilitud. Dado que \(\phi>0)\), el modelo beta-binomial no puede modelar datos con subdispersión.
7.6.2 Estudio de teratología
Para los datos del estudio de teratología se puede proponer un modelo binomial en un principio: \[ y_i^* = n_i y_i \sim \mbox{binomial} (n_i, \pi_i), \] donde \(n_i\) y \(y_i\) es el tamaño y la proporción de fetos muertos de la camada \(i\). Además, se tiene que: \[ \mbox{logit }\pi_i = \beta_0 + \mbox{hb}_i \beta_1 + \mbox{treat}_{2i} \beta_2 + \mbox{treat}_{3i}\beta_3 + \mbox{treat}_{4i} \beta_4. \] El ajuste del modelo es:
data(lirat,package = 'VGAM')
modlirat.binom = glm(cbind(R,N-R)~hb+as.factor(grp),family=binomial,data=lirat)
summary(modlirat.binom)##
## Call:
## glm(formula = cbind(R, N - R) ~ hb + as.factor(grp), family = binomial,
## data = lirat)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.1795 0.5056 4.311 1.63e-05 ***
## hb -0.2190 0.1020 -2.148 0.031728 *
## as.factor(grp)2 -2.4748 0.5045 -4.906 9.30e-07 ***
## as.factor(grp)3 -3.1527 0.9433 -3.342 0.000832 ***
## as.factor(grp)4 -2.0520 1.0629 -1.931 0.053525 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 509.43 on 57 degrees of freedom
## Residual deviance: 168.91 on 53 degrees of freedom
## AIC: 250.38
##
## Number of Fisher Scoring iterations: 5La evaluación de sobredispersión la podemos hacer usando la razón entre el estadístico \(\chi^2\) de Pearson y los grados de libertad:
## [1] 2.93993Dado que esta razón es aproximadamente \(3\), los datos presentan sobredispersión. Por lo tanto es mas conveniente proponer un modelo beta-binomial:
\[
y_i^{*}\sim \mbox{beta-binomial}(n_i,\pi_i,\phi),
\]
con
\[
\mbox{logit }\pi_i = \beta_0 + \mbox{hb}_i \beta_1 + \mbox{treat}_{2i} \beta_2 + \mbox{treat}_{3i}\beta_3 + \mbox{treat}_{4i} \beta_4.
\]
En R el modelo beta-binomial se puede estimar utilizando la función betabin de la librería aod:
library(aod)
modlirat.betabinom =betabin(cbind(R,N-R)~hb+as.factor(grp),data=lirat,random=~1)
modlirat.betabinom## Beta-binomial model
## -------------------
## betabin(formula = cbind(R, N - R) ~ hb + as.factor(grp), random = ~1,
## data = lirat)
##
## Convergence was obtained after 433 iterations.
##
## Fixed-effect coefficients:
## Estimate Std. Error z value Pr(> |z|)
## (Intercept) 2.130e+00 8.676e-01 2.455e+00 1.408e-02
## hb -1.694e-01 1.772e-01 -9.557e-01 3.392e-01
## as.factor(grp)2 -2.441e+00 8.508e-01 -2.869e+00 4.113e-03
## as.factor(grp)3 -2.836e+00 1.329e+00 -2.134e+00 3.287e-02
## as.factor(grp)4 -2.285e+00 1.817e+00 -1.258e+00 2.085e-01
##
## Overdispersion coefficients:
## Estimate Std. Error z value Pr(> z)
## phi.(Intercept) 2.356e-01 6.041e-02 3.9e+00 4.813e-05
##
## Log-likelihood statistics
## Log-lik nbpar df res. Deviance AIC AICc
## -9.302e+01 6 52 1.146e+02 1.98e+02 1.997e+02Las estimaciones de los coeficientes del modelo beta-binomial son similares a los del modelo binomial. Sin embargo, los errores estándar son mas grandes. Esto último es debido al efecto de la sobredispersión (\(\widehat{\phi}=0.236\) indica una correlación positiva entre los fetos que pertenecen a la misma camada). Además, el efecto del tratamiento #4 no es significativamente diferente al placebo.
Podemos evaluar sobredispersión de nuevo:
## Warning in model.matrix.default(mt, mfb, contrasts): non-list contrasts
## argument ignored## [1] 0.9287516La razón está cercana a \(1\) por lo que la varianza está mejor modelada por la distribución beta-binomial. La comparación de los ajustes se puede hacer a través de criterios de información:
## [1] 250.3777## df AIC AICc
## modlirat.betabinom 6 198.0319 199.6789Observando los valores del AIC podemos determinar que el modelo beta-binomial presenta mejor ajuste.