Capítulo 4 Selección de variables

4.1 Ejemplos

4.1.1 Unidad quirúrgica

Una unidad quirúrgica de un hospital está interesada en predecir la supervivencia de los pacientes sometidos a un tipo particular de operación hepática. Se dispuso de una selección aleatoria de \(108\) pacientes para el análisis. De cada registro del paciente, se extrajo la siguiente información de la evaluación preoperatoria:

• bcs: coagulación sanguínea.

• pindex: índice de pronóstico.

• enzyme: función enzimática.

• liver_test: función hepática.

• age: edad.

• gender: genero (0 = masculino, 1 = femenino).

• alc_mod: historial de consumo de alcohol (0 = Ninguno, 1 = Moderado).

• alc_heavy: & historial de consumo de alcohol (0 = Ninguno, 1 = Fuerte).

• y: tiempo de supervivencia.

El objetivo del estudio es determinar los factores que influyen sobre el tiempo de supervivencia (que se determinó posteriormente) en función de las demás variables.

El modelo propuesto es el siguiente: \[\begin{equation} \begin{split} \log y_{i} =& \beta_{0}+\mbox{bcs}_{i}\beta_{1} + \mbox{pindex}_{i}\beta_{2}+ \mbox{enzyme}_{i}\beta_{3} + \mbox{liver}_{i}\beta_{4} + \mbox{age}_{i}\beta_{5} + \mbox{gender}_{i}\beta_{6}+ \\ & \mbox{alc_mod}_{i}\beta_{7} + \mbox{alc_heavy}_{i}\beta_{8} + \varepsilon_{i} \end{split} \nonumber \end{equation}\]

El ajuste del modelo es:

library(olsrr)
data(surgical)
surgical$log.y = log(surgical$y)
mod.surgical.completo = lm(log.y~bcs+pindex+enzyme_test+liver_test+age+gender+alc_mod+alc_heavy,data=surgical)
summary(mod.surgical.completo)

## 
## Call:
## lm(formula = log.y ~ bcs + pindex + enzyme_test + liver_test + 
##     age + gender + alc_mod + alc_heavy, data = surgical)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.35555 -0.13849 -0.05179  0.14912  0.46349 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.050949   0.251741  16.092  < 2e-16 ***
## bcs          0.068551   0.025420   2.697  0.00982 ** 
## pindex       0.013459   0.001947   6.913 1.37e-08 ***
## enzyme_test  0.014948   0.001809   8.261 1.44e-10 ***
## liver_test   0.007931   0.046706   0.170  0.86592    
## age         -0.003567   0.002751  -1.296  0.20145    
## gender       0.084151   0.060746   1.385  0.17279    
## alc_mod      0.057313   0.067480   0.849  0.40019    
## alc_heavy    0.388190   0.088374   4.393 6.73e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2093 on 45 degrees of freedom
## Multiple R-squared:  0.8461, Adjusted R-squared:  0.8187 
## F-statistic: 30.93 on 8 and 45 DF,  p-value: 7.823e-16

4.1.2 Grasa corporal

La medición de la grasa corporal es un proceso complejo. Dado que los músculos y los huesos son más densos, el calculo de % de grasa corporal se basa, entre otros aspectos, en la medición de la densidad corporal la cuál requiere sumergir a las personas en el agua. Por esta razón, se quiere buscar un método más sencillo para determinarlo. Para esto, se registraron la edad, el peso, la altura y \(10\) medidas de la circunferencia corporal de \(252\) hombres. De igual forma, a cada uno de estos hombres se les midió el % de grasa corporal de forma precisa (usando la ecuación de Brozek, medición a partir de la densidad).

Cómo variable respuesta se utiliza la medición por el método de Brozek, y las posibles covariables son:

• age: edad (en años).

• weight: peso (en libras).

• height: altura (en pulgadas).

• neck: circunferencia del cuello (en centímetros).

• chest: circunferencia del pecho (en centímetros).

• abdom: circunferencia del abdomen (en centímetros).

• hip: circunferencia de la cadera (en centímetros).

• thigh:circunferencia del muslo (en centímetros).

• knee:circunferencia de la rodilla (en centímetros).

• ankle:circunferencia del tobillo (en centímetros).

• biceps: circunferencia del bíceps extendido (en centímetros).

• forearm: circunferencia del antebrazo (en centímetros).

• wrist: circunferencia de la muñeca (en centímetros).

El modelo propuesto es el siguiente: \[\begin{equation} \mbox{brozek}_i = \beta_{0} + \mbox{age}_i\beta_1+ \mbox{weight}_i\beta_2 + \ldots + \mbox{wrist}_i\beta_{13} + \varepsilon_i. \tag{4.1} \end{equation}\] El ajuste del modelo es:

library(faraway)
data(fat)
mod.fat <- lm(brozek ~ age + weight + height + neck + chest + abdom +
             hip + thigh + knee + ankle + biceps + forearm + wrist, data=fat)
summary(mod.fat)

## 
## Call:
## lm(formula = brozek ~ age + weight + height + neck + chest + 
##     abdom + hip + thigh + knee + ankle + biceps + forearm + wrist, 
##     data = fat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -10.264  -2.572  -0.097   2.898   9.327 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -15.29255   16.06992  -0.952  0.34225    
## age           0.05679    0.02996   1.895  0.05929 .  
## weight       -0.08031    0.04958  -1.620  0.10660    
## height       -0.06460    0.08893  -0.726  0.46830    
## neck         -0.43754    0.21533  -2.032  0.04327 *  
## chest        -0.02360    0.09184  -0.257  0.79740    
## abdom         0.88543    0.08008  11.057  < 2e-16 ***
## hip          -0.19842    0.13516  -1.468  0.14341    
## thigh         0.23190    0.13372   1.734  0.08418 .  
## knee         -0.01168    0.22414  -0.052  0.95850    
## ankle         0.16354    0.20514   0.797  0.42614    
## biceps        0.15280    0.15851   0.964  0.33605    
## forearm       0.43049    0.18445   2.334  0.02044 *  
## wrist        -1.47654    0.49552  -2.980  0.00318 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.988 on 238 degrees of freedom
## Multiple R-squared:  0.749,  Adjusted R-squared:  0.7353 
## F-statistic: 54.63 on 13 and 238 DF,  p-value: < 2.2e-16

4.2 Problema de selección de variables

En problemas de regresión se tiene un conjunto grande de potenciales covariables. Si ajustamos un modelo considerandolas todas podemos estar incluyendo covariables que son irrelevante. Por el otro lado, si no las incluimos todas es posible que estemos omitiendo covariables importantes. En ambos casos hay consecuencias negativas.

Para illustrar esto, considere el siguiente modelo: \[\begin{equation} \begin{split} y_{i} &= \beta_{0} + \sum_{j=1}^{p-1}\beta_{j}x_{ij} + \varepsilon_{i} \\ &= \beta_{0} + \sum_{j=1}^{r}\beta_{j}x_{ij} + \sum_{j=r+1}^{p-1}\beta_{j}x_{ij} + \varepsilon_{i} \\ &= \boldsymbol x_{1i}'\boldsymbol \beta_1 + \boldsymbol x_{2i}'\boldsymbol \beta_2 + \varepsilon_i, \end{split} \tag{4.2} \end{equation}\] donde \(\boldsymbol x_{1i} = (1,x_{1i},x_{2i},\ldots,x_{ri})\), \(\boldsymbol x_{2i} = (x_{r+1,i},x_{r+2,i},\ldots,x_{p-1,i})\), \(\boldsymbol \beta_1 = (\beta_0,\beta_1,\beta_2,\ldots,\beta_r)'\), \(\boldsymbol \beta_2 = (\beta_{r+1},\beta_{r+2},\ldots,\beta_{p-1})'\), y \(\varepsilon_i \sim N(0,\sigma^{2})\). Es decir, se hace una partición de las covariables y los coeficientes de regresión en dos componentes.

En forma matricial, el modelo es: \[ \boldsymbol y= \boldsymbol X_{1}\boldsymbol \beta_{1} + \boldsymbol X_{2}\boldsymbol \beta_{2}+ \boldsymbol \varepsilon, \] donde \(\boldsymbol X_{1}\) es una matriz \(n \times r\) con la \(i\)-ésima fila igual a \(\boldsymbol x_{1i}\) y \(\boldsymbol X_{2}\) es una matriz \(n \times (p-r-1)\) con la \(i\)-ésima fila igual a \(\boldsymbol x_{2i}\).

4.2.1 ¿Qué pasa si ignoramos covariables importantes?

Ahora, considere que el modelo generador de datos es (4.2), pero decidimos estimar: \[ y_{i} = \boldsymbol x_{1i}'\boldsymbol \beta_1 + \varepsilon_i. \] Es decir, estamos omitiendo \(\boldsymbol x_{2i}\) del modelo (puesto que \(\boldsymbol \beta_2 \neq 0\), estas covariables son relevantes). El estimador por MCO de \(\boldsymbol \beta_1\) es: \[ \widehat{\boldsymbol \beta}_{1} = (\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'\boldsymbol y. \] De aquí tenemos que \(E(\widehat{\boldsymbol \beta}_{1}) = \boldsymbol \beta_{1} + (\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'\boldsymbol X_{2}\boldsymbol \beta_{2}\). Es decir que \(\widehat{\boldsymbol \beta}_{1}\) es un estimador sesgado, a menos que \(\boldsymbol X_{1}'\boldsymbol X_{2} = \boldsymbol 0\) (las columnas de \(X_{1}\) son ortogonales a las columnas de \(X_{2}\)).

De igual forma, las predicciones también serán sesgadas. La predicción en el punto \(\boldsymbol x_{01}\) es: \[ \widehat{y}_{0} = \boldsymbol x_{01}'\widehat{\boldsymbol \beta}_{1}. \] Su valor esperado es: \[ E(\widehat{y}_{0}) = \boldsymbol x_{01}'\boldsymbol \beta_{1} + \boldsymbol x_{01}'(\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'\boldsymbol X_{2}\boldsymbol \beta_{2} \neq \boldsymbol x_{01}'\beta_{1} + \boldsymbol x_{02}'\beta_{2}. \] Por lo tanto, si omitimos variables relevantes obtenemos sesgo en las estimaciones.

4.2.2 ¿Que pasa si incluimos covariables irrelevantes?

Ahora, consideremos el caso en que \(\boldsymbol \beta_2=0\), es decir, las covariables \(\boldsymbol x_{2}\) no tienen un aporte significativo en el modelo. Pero decidimos estimar el modelo completo.

En este caso, el estimador de \(\boldsymbol \beta\) es: \[ \widehat{\boldsymbol \beta}= (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y= \begin{pmatrix} \boldsymbol X_{1}'\boldsymbol X_{1} & \boldsymbol X_{1}\boldsymbol X_{2} \\ \boldsymbol X_{2}'\boldsymbol X_{1} & \boldsymbol X_{2}'\boldsymbol X_{2} \end{pmatrix}^{-1} \begin{pmatrix} \boldsymbol X_{1}' \\ \boldsymbol X_{2}' \end{pmatrix}\boldsymbol y. \] El Valor esperado de \(\widehat{\boldsymbol \beta}\) es: \[\begin{equation} \begin{split} E(\widehat{\boldsymbol \beta}) =& (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'E(\boldsymbol y) = (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol X_{1}\boldsymbol \beta_1 \\ = & (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'(\boldsymbol X_{1} \ \boldsymbol X_{2}) \begin{pmatrix} \boldsymbol \beta_1 \\ \boldsymbol 0 \end{pmatrix} = \begin{pmatrix} \boldsymbol \beta_1 \\ \boldsymbol 0 \end{pmatrix}. \end{split} \nonumber \end{equation}\] Es decir que \(\widehat{\boldsymbol \beta}\) es un estimador insesgado.

La varianza de \(\widehat{\boldsymbol \beta}\) es: \[\begin{equation} \begin{split} V(\widehat{\boldsymbol \beta}) =& \sigma^{2}(\boldsymbol X'\boldsymbol X)^{-1} = \sigma^{2}\begin{pmatrix} \boldsymbol X_{1}'\boldsymbol X_{1} & \boldsymbol X_{1}\boldsymbol X_{2} \\ \boldsymbol X_{2}'\boldsymbol X_{1} & \boldsymbol X_{2}'\boldsymbol X_{2} \end{pmatrix}^{-1} \\ =& \sigma^{2} \begin{pmatrix} (\boldsymbol X_{1}'\boldsymbol X_{1})^{-1} + \boldsymbol L\boldsymbol M\boldsymbol L& - \boldsymbol L\boldsymbol M\\ -\boldsymbol M\boldsymbol L' & \boldsymbol M \end{pmatrix}, \end{split} \nonumber \end{equation}\] donde \(\boldsymbol L= (\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'\boldsymbol X_{2}\) y \(\boldsymbol M= \boldsymbol X_{2}'(\boldsymbol I- \boldsymbol H_{1})\boldsymbol X_{2}\). Particularmente, para \(\widehat{\boldsymbol \beta}_1\) tenemos que: \[ V(\widehat{\boldsymbol \beta}_{1}) = \sigma^{2} \left[ (\boldsymbol X_{1}'\boldsymbol X_{1})^{-1} + \boldsymbol L\boldsymbol M\boldsymbol L\right]. \] Dado que \(\boldsymbol M\) (y por lo tanto \(\boldsymbol L\boldsymbol M\boldsymbol L\)) es positiva-definida, la varianza de \(\widehat{\boldsymbol \beta}_{1}\) se infla al incluir las covariables irrelevantes al modelo. La única excepción es cuando las columnas de \(\boldsymbol X_{1}\) y \(\boldsymbol X_{2}\) son ortogonales.

De igual forma, las predicciones en el punto \(\boldsymbol x_{0}' = (\boldsymbol x_{01}' \ \boldsymbol x_{02}')\) son insesgadas: \[ E(\widehat{y}_{0}) = E(\boldsymbol x_{0}'\widehat{\boldsymbol \beta}) = (\boldsymbol x_{01}' \ \boldsymbol x_{02}')\begin{pmatrix} \boldsymbol \beta_{1} \\ \boldsymbol 0 \end{pmatrix} = \boldsymbol x_{01}'\boldsymbol \beta_{1}. \] En conclusión:

• Cuando omitimos covariables relevantes, obtenemos sesgos en las estimaciones.

• Cuando incluimos covariables irrelevantes, se inflan las varianzas de las estimaciones.

4.3 Métodos para la selección de variables

Si tenemos \((p-1)\) covariables, entonces hay \((p-1)^2\) modelos posibles. Por lo que podemos ajustar todos los posibles modelos y hacer una comparación entre ellos usando algunos criterios de decisión.

Existen varios criterios para determinar que modelo es “mejor” que otro y este debe escogerse teniendo en cuenta cuál es el objetivo que se tiene al ajustar el modelo (descripción de la relación, predicción, control, etc.). Algunos de estos criterios son el coeficiente de determinación (\(R^{2}\) y \(R^{2}_{adj}\)), el estadístico \(C_{p}\) de Mallows, el estadístico PRESS y el \(R^{2}\) de predicción, los criterios de información (AIC y BIC).

4.3.1 Coeficiente de determinación

Esté indicador está definido como: \[ R^{2} = \frac{SS_{\mbox{reg}}}{SS_{\mbox{T}}} = 1 - \frac{SS_{\mbox{res}}}{SS_{\mbox{T}}}. \] El \(R^{2}\) cuantifica la cantidad de variabilidad de la variable respuesta que es explicada por el modelo. Se tiene que \(0 \leq R^{2} \leq 1\). Valores más cercanos a \(1\) implican que el modelo explica gran parte de la variabilidad de \(y\). Hay que tener en cuenta que el \(R^{2}\) siempre crece a medida que se adicionan más covariables al modelo. Por lo tanto, se puede puede agregar regresores hasta el punto en que una covariable adicional no propociona un aumento considerable en el \(R^{2}\).

4.3.2 Coeficiente de determinación ajustado

Para evitar el incoviente del \(R^{2}\), se puede utlizar el el coeficiente de determinación ajustado definido como: \[ R^{2}_{adj} = 1 - \frac{n-1}{n-p}\frac{SS_{\mbox{res}}}{SS_{\mbox{T}}} = 1- \frac{MS_{\mbox{res}}}{SS_{\mbox{T}}/(n-1)} = 1- \frac{n-1}{n-p}(1-R^{2}). \] El \(R^{2}_{adj}\) no necesariamente aumenta al adicionar nuevos términos al modelo. Este solo aumenta si hay una disminución del \(MS_{\mbox{res}}\).

4.3.3 C\(_p\) de Mallows

Mallows propone un criterio basado en el error cuadrático medio (ECM) de \(\widehat{y}_i\), esto es: \[ E[\widehat{y}_{i}- E(y_{i})]^2 = [E(y_{i}) - E(\widehat{y}_{i})]^2 + V(\widehat{y}_{i}), \] donde \(E(y_{i})\) es el valor esperado de la respuesta (‘modelo real’), y \(E(\widehat{y}_{i})\) es el valor esperado de la respuesta basado en el modelo propuesto (basado en \(p\) covariables).

El ECM total estandarizado está definido como: \[\begin{equation} \begin{split} \Gamma_{p} =& \frac{1}{\sigma^{2}}\left\{\sum_{i=1}^{n}[E(y_{i}) - E(\widehat{y}_{i})]^2 + \sum_{i=1}^{n} V(\widehat{y}_{i}) \right\} \\ =& \frac{1}{\sigma^{2}}\left\{SS_{B}(p) + \sum_{i=1}^{n} V(\widehat{y}_{i}) \right\} = \frac{1}{\sigma^{2}}\left\{SS_{B}(p) + p\sigma^{2} \right\} \\ =& \frac{1}{\sigma^{2}}\left\{ E[SS_{\mbox{res}}(p)] - (n-p)\sigma^{2} + p\sigma^{2} \right\} \\ =& \frac{E[SS_{\mbox{res}}(p)]}{\sigma^{2}} - n + 2p. \end{split} \nonumber \end{equation}\]

Reemplazando \(E[SS_{\mbox{res}}(p)]\) por \(SS_{\mbox{res}}(p)\), y asumiendo que \(MS_{\mbox{res}}(p^{*})\) (calculado usando el modelo completo) es un buen estimador de \(\sigma^{2}\): \[ C_{p} = \frac{SS_{\mbox{res}}(p)}{MS_{\mbox{res}}(p^{*})} - n + 2p. \] Por lo tanto, para el modelo completo \(C_{p} = p^{*}\). Si \(E[SS_{\mbox{res}}(p)] = (n-p)\sigma^{2}\) (asumiendo que \(SS_{B}(p)=0\)), tenemos que: \[ E[C_{p}| \mbox{Sesgo}=0] = \frac{(n-p)\sigma^{2}}{\sigma^{2}} - n +2p = p. \] Si el modelo propuesto es insesgado se espera que el \(C_p\) esté cercano a \(p\). Aunque se espera que el \(C_p=p\), es deseable que \(C_p < p\). Por lo tanto, modelos con valores pequeños de \(C_p\) son mejores.

4.3.4 Estadístico PRESS

El estadístico PRESS (prediction error sum of squares) está definido como: \[ \mbox{PRESS} = \sum_{i=1}^{n} (y_{i} - \widehat{y}_{(i)})^{2} = \sum_{i=1}^{n} \left( \frac{e_{i}}{1-h_{ii}} \right)^{2}. \] Para comparar modelos, menor valor del PRESS indica que el modelo es mejor para hacer predicciones. A partir del PRESS se puede calcular el \(R^{2}\) de predicción: \[ R^{2}_{pred} = 1 - \frac{PRESS}{SST}. \] Basado en este criterio, mayor es el valor de \(R^{2}_{pred}\) mejor es el modelo para hacer predicciones. La ventaja del PRESS y \(R_{pred}^{2}\) es que evitan el sobreajuste dado que se calculan utilizando observaciones no incluidas en la estimación del modelo.

4.3.5 Criterios de información

La idea es comparar modelos estimados teniendo en cuenta la bondad de ajuste del modelo (verosimilitud, \(L\)) y su complejidad (número de parámetros). El criterio de información de Akaike está definido como: \[ \mbox{AIC} = -2\log (L) + 2p. \] El criterio de información bayesiano (o de Schwarz - SBC): \[ \mbox{BIC} = -2\log (L) + p\log n. \] Es preferible modelos con valores menores de AIC o BIC. Dado que la penalización del BIC es mayor (si \(n > 7\)), este indicador prefiere modelos con menor número de covariables.

Recordemos que la log-verosimilitud es: \[ \log L(\boldsymbol \beta,\sigma^{2}) = - \frac{n}{2}\log (2\pi) - n\log(\sigma) - \frac{1}{2\sigma^{2}}(\boldsymbol y- \boldsymbol X\boldsymbol \beta)'(\boldsymbol y-\boldsymbol X\boldsymbol \beta). \] El estimador por máxima verosimilitud de \(\sigma^{2}\) es \(\widehat{\sigma}=SS_{\mbox{res}}/n\). Por lo tanto, el máximo valor de la log-verosimilitud es: \[ \log L(\widehat{\boldsymbol \beta},\widehat{\sigma}^{2}) = -\frac{n}{2}\log (2\pi) - \frac{n}{2}\log\widehat{\sigma}^{2} - \frac{1}{2\widehat{\sigma}^{2}}SS_{\mbox{res}}= -\frac{n}{2}\log (SS_{\mbox{res}}/n) + \mbox{constante}. \] Por lo tanto: \[ AIC \propto n\log(SS_{\mbox{res}}/n) + 2p \mbox{ y } BIC \propto n\log(SS_{\mbox{res}}/n) + p\log n. \] Hay varias adaptaciones de estos criterios de información definiendo diferentes penalizaciones.

4.4 Comparación de los modelos

4.4.1 Todos los posibles modelos

Con la función ols_step_all_possible() de la librería olsrr es posible ajustar todos posibles modelos y determinar el mejor bajo diferentes criterios. Otra alternativa es la función regsubsets() de la librería leaps. Está función es más rápida (se basa en un algoritmo más eficiente), pero no es user-friendly.

4.4.1.1 Datos de unidad quirúrgica

A través de la función ols_step_all_possible podemos ajustar los \(255\) modelos que se pueden ajustar usando las ocho posibles covariables:

surgical.all.mods=ols_step_all_possible(mod.surgical.completo)

Además de ajustar los modelos, se calculan varios criterios (\(R^{2}\),\(R^{2}_{adj}\), \(R^{2}_{pred}\),AIC,BIC,…) para cada uno de ellos.

Puesto que son muchos modelos, podemos organizar los resultados de tal forma que obtengamos los mejores modelos basándonos en cada uno de los criterios. Por ejemplo, los 5 mejores ajustes según el \(R^{2}_{adj}\) son:

R2adj.order = order(surgical.all.mods$result$adjr,decreasing = T)
as.data.frame(surgical.all.mods$result)[R2adj.order[1:5],c(2:8,10)]

##     n                                             predictors   rsquare
## 226 6            bcs pindex enzyme_test age gender alc_heavy 0.8434664
## 251 7    bcs pindex enzyme_test age gender alc_mod alc_heavy 0.8460095
## 171 5                bcs pindex enzyme_test gender alc_heavy 0.8374622
## 248 7 bcs pindex enzyme_test liver_test age gender alc_heavy 0.8436412
## 169 5                   bcs pindex enzyme_test age alc_heavy 0.8358522
##          adjr      rmse   predrsq       cp      sbic
## 226 0.8234834 0.1926586 0.7836037 5.772458 -159.4064
## 251 0.8225761 0.1910872 0.7806940 7.028837 -157.6344
## 171 0.8205312 0.1963187 0.7827597 5.528174 -160.2288
## 248 0.8198474 0.1925510 0.7749807 7.721367 -157.0871
## 169 0.8187535 0.1972887 0.7862369 5.998959 -159.8244

Basándonos en este criterio el mejor ajuste se obtiene considerando las covariables bcs, pindex, enzyme_test, age, gender, y alc_heavy. Es decir, eliminando las covariables función hepática y consumo de alcohol moderado. Note que no todos los demás críterios sugieren el mismo modelo. Si eliminamos las covariables gender obtenemos un modelo con un \(R^{2}_{pred}\) más alto.

Ahora, si nos apoyamos en el AIC, los mejores 5 ajustes son:

AIC.order = order(surgical.all.mods$result$aic,decreasing = F)
as.data.frame(surgical.all.mods$result)[AIC.order[1:5],c(2:8,10)]

##     n                                          predictors   rsquare      adjr
## 226 6         bcs pindex enzyme_test age gender alc_heavy 0.8434664 0.8234834
## 171 5             bcs pindex enzyme_test gender alc_heavy 0.8374622 0.8205312
## 97  4                    bcs pindex enzyme_test alc_heavy 0.8299187 0.8160345
## 169 5                bcs pindex enzyme_test age alc_heavy 0.8358522 0.8187535
## 251 7 bcs pindex enzyme_test age gender alc_mod alc_heavy 0.8460095 0.8225761
##          rmse   predrsq       cp      sbic
## 226 0.1926586 0.7836037 5.772458 -159.4064
## 171 0.1963187 0.7827597 5.528174 -160.2288
## 97  0.2008227 0.7862922 5.733992 -160.5329
## 169 0.1972887 0.7862369 5.998959 -159.8244
## 251 0.1910872 0.7806940 7.028837 -157.6344

Con este críterio se escoge el mismo modelo que con el \(R^{2}_{adj}\). Sin embargo, podemos observar que el BIC sugiere eliminar la covariable asociada a la edad.

En la Figura 4.2 muestra los \(R^{2}\),\(R^{2}_{adj}\), \(R^{2}_{pred}\),C\(_p\), AIC y BIC (SBC) para todos los posibles ajustes. Note que, dentro de cada subgrupo de modelos (determinado por el número de covariables), los criterios eligen los modelos en el mismo orden. La diferencia está en el número de covariables a elegir. Generalmente, el BIC prefiere modelos más parsimoniosos. Esto no ocurre con criterios de validación cruzada, como el PRESS o \(R^{2}_{pred}\).

par(mfrow=c(1,2))
plot(surgical.all.mods)

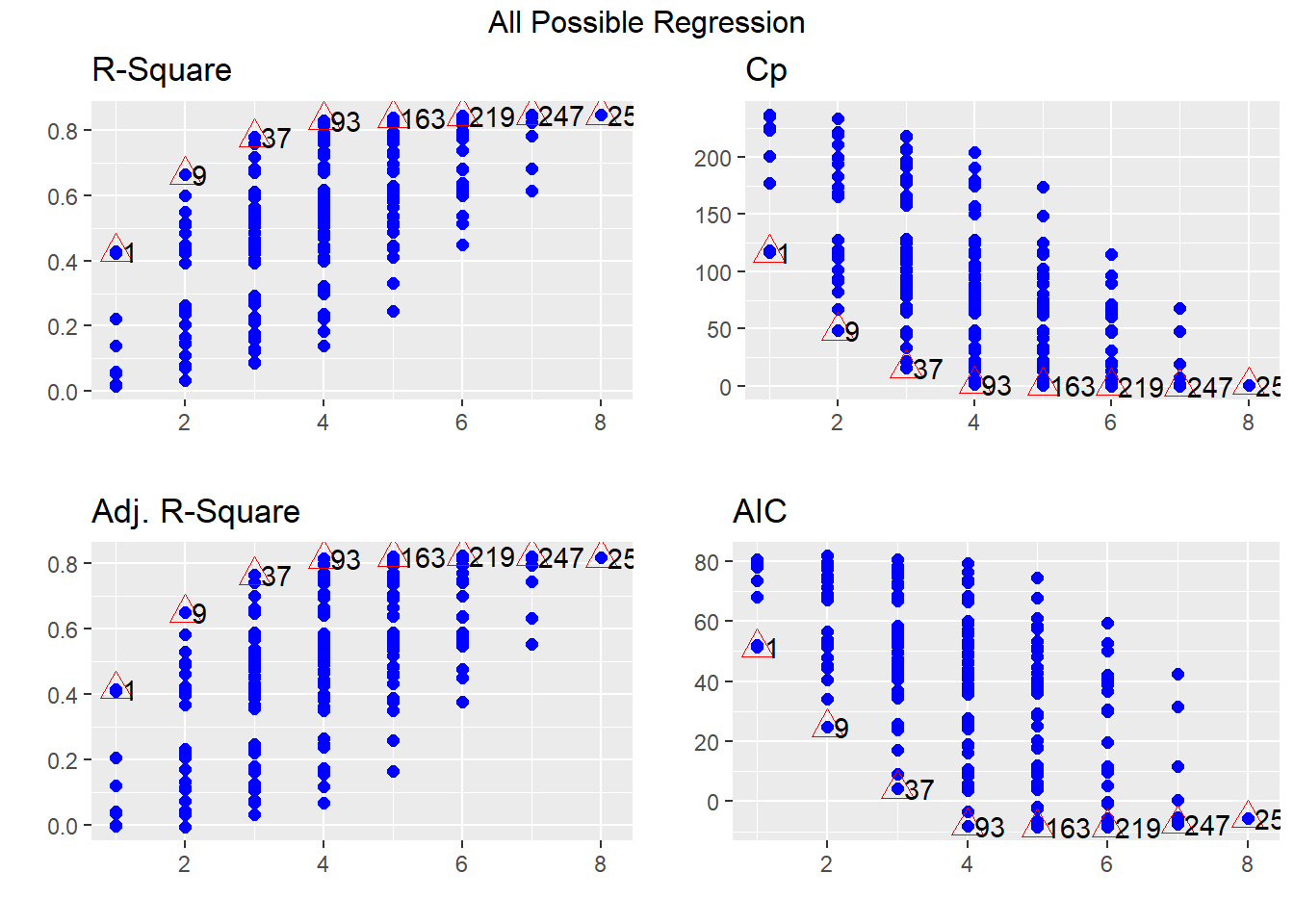
Figure 4.1: Valores de los criterios de selección calculados para cada uno de todos los posibles modelos.

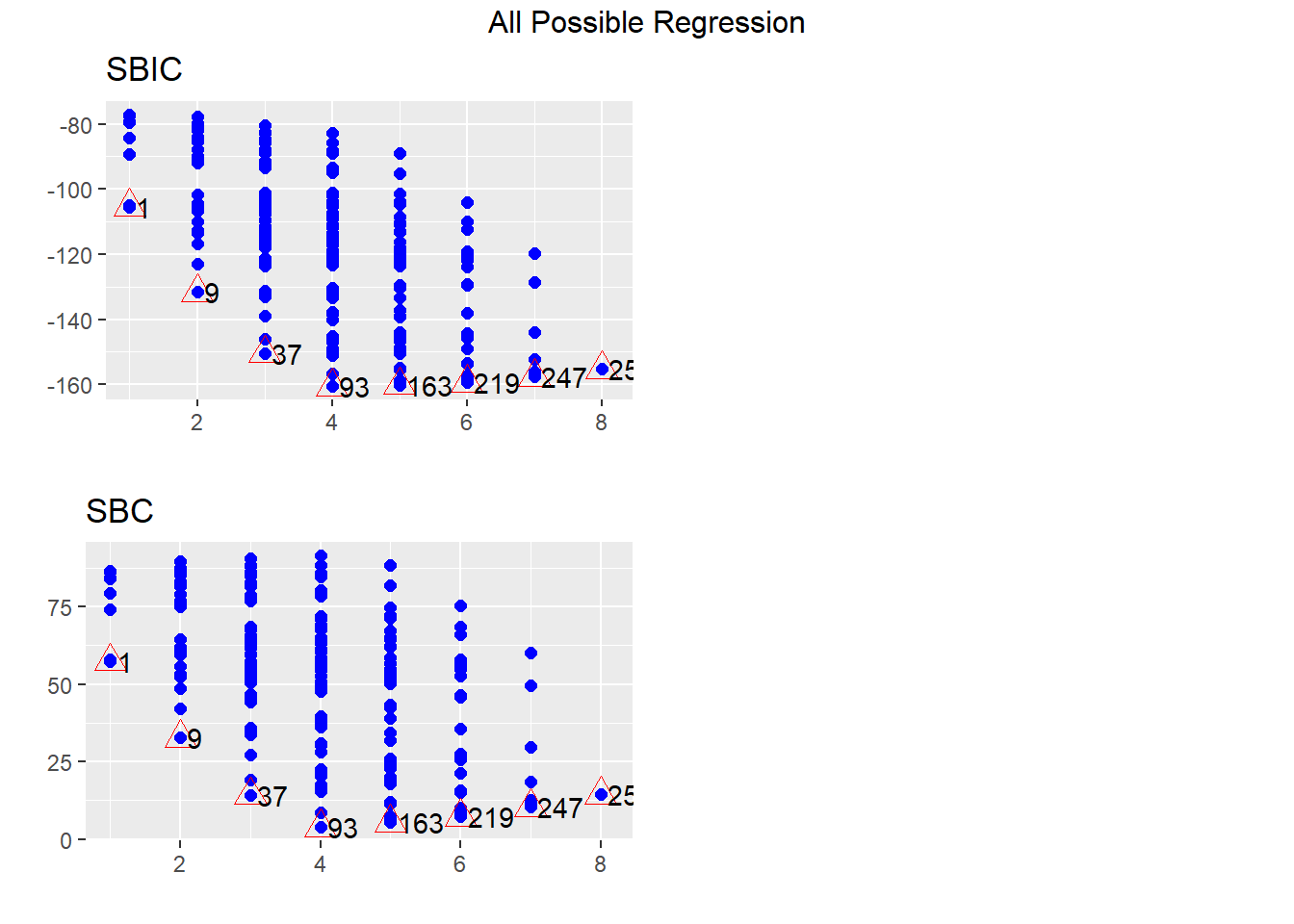
Figure 4.2: Valores de los criterios de selección calculados para cada uno de todos los posibles modelos.

Teniendo en cuenta esto, con la función ols_step_best_subset() selecciona el mejor modelo para cada subconjunto de número de covariables basándose en los diferentes criterios:

ols_step_best_subset(mod.surgical.completo)

##                            Best Subsets Regression                           
## -----------------------------------------------------------------------------
## Model Index    Predictors
## -----------------------------------------------------------------------------
##      1         enzyme_test                                                    
##      2         pindex enzyme_test                                             
##      3         pindex enzyme_test alc_heavy                                   
##      4         bcs pindex enzyme_test alc_heavy                               
##      5         bcs pindex enzyme_test gender alc_heavy                        
##      6         bcs pindex enzyme_test age gender alc_heavy                    
##      7         bcs pindex enzyme_test age gender alc_mod alc_heavy            
##      8         bcs pindex enzyme_test liver_test age gender alc_mod alc_heavy 
## -----------------------------------------------------------------------------
## 
##                                                    Subsets Regression Summary                                                   
## --------------------------------------------------------------------------------------------------------------------------------
##                        Adj.        Pred                                                                                          
## Model    R-Square    R-Square    R-Square      C(p)        AIC        SBIC         SBC       MSEP      FPE       HSP       APC  
## --------------------------------------------------------------------------------------------------------------------------------
##   1        0.4273      0.4162      0.3496    117.4783    51.4343    -105.4395    57.4013    7.6160    0.1463    0.0028    0.6168 
##   2        0.6632      0.6500      0.6044     50.4918    24.7668    -131.5971    32.7228    4.5684    0.0893    0.0017    0.3765 
##   3        0.7780      0.7647      0.7291     18.9015     4.2432    -150.4023    14.1881    3.0718    0.0610    0.0012    0.2575 
##   4        0.8299      0.8160      0.7863      5.7340    -8.1306    -160.5329     3.8033    2.4030    0.0486     9e-04    0.2048 
##   5        0.8375      0.8205      0.7828      5.5282    -8.5803    -160.2288     5.3426    2.3453    0.0482     9e-04    0.2032 
##   6        0.8435      0.8235      0.7836      5.7725    -8.6129    -159.4064     7.2990    2.3077    0.0482     9e-04    0.2032 
##   7        0.8460      0.8226      0.7807      7.0288    -7.4974    -157.6344    10.4035    2.3207    0.0492    0.0010    0.2076 
##   8        0.8461      0.8187      0.7711      9.0000    -5.5320    -155.2573    14.3579    2.3719    0.0511    0.0010    0.2154 
## --------------------------------------------------------------------------------------------------------------------------------
## AIC: Akaike Information Criteria 
##  SBIC: Sawa's Bayesian Information Criteria 
##  SBC: Schwarz Bayesian Criteria 
##  MSEP: Estimated error of prediction, assuming multivariate normality 
##  FPE: Final Prediction Error 
##  HSP: Hocking's Sp 
##  APC: Amemiya Prediction Criteria

A partir de estos resultados, y con la ayuda de expertos en el tema, se puede hacer una selección del mejor modelo para hacer las predicciónes.

4.4.2 Algorítmos de selección

Para el proceso de selección, la mejor opción es evaluar todos los posibles modelos. Sin embargo, en la presencia de muchas posibles covariables este proceso puede requerir una carga computacional muy alta. Por esta razón, se han desarrollado varios algoritmos para evaluar solo un subconjunto de modelos agregando o eliminando covariables una a la vez.

4.4.2.1 Selección hacia delante (forward selection)

Este algoritmo parte del modelo sin ninguna covariable (es decir, solo el intercepto) y el ajuste ``óptimo’’ se encuentra ingresando covariables una a la vez basándose en algún criterio (por ejemplo AIC).

La primera covariable se escoge luego de ajustar los \((p-1)\) modelos simples con cada uno de los regresores. Por ejemplo, seleccionado la covariable que proporciona el mejor AIC.

Luego se ajustan los modelos combinando la covariable previamente seleccionada con cada una de los restantes \((p-2)\) regresores. Si el mejor ajuste con dos covariables proporcina un menor AIC que en el paso anterior, continuamos seleccionando la tercer covariable de la misma forma.

El algoritmo continua seleccionando covariables hasta que se satisface un criterio de parada (por ejemplo, hasta que el AIC aumente).

4.4.2.2 Selección hacia atrás (backward selection)

Aquí se empieza evaluando el modelo con todas las covariables candidatas y se van eliminando covariables una a una hasta que un criterio de parada se satisface (por ejemplo, hasta que el AIC aumenta).

4.4.2.3 Selección por segmentos (stepwise selection)

Aquí se siguen los mismos pasos que la selección hacia delante. Pero en cada paso se evalúan de nuevo los candidatos que ya habían ingresado en el modelo. Por lo tanto, una covariable que ya esté en el modelo puede ser eliminada en algún paso posterior.

4.4.2.4 Unidad quirúrgica

Consideremos el modelo anterior adicionando las interacciones de las covariables continuas con las categóricas: \[\begin{equation} \begin{split} \log y_{i} =& \beta_{0}+\mbox{bcs}_{i}\beta_{1} + \mbox{pindex}_{i}\beta_{2}+ \mbox{enzyme}_{i}\beta_{3} + \mbox{liver}_{i}\beta_{4} + \mbox{age}_{i}\beta_{5} + \mbox{gender}_{i}\beta_{6}+ \mbox{alc_mod}_{i}\beta_{7} + \\ & \mbox{alc_heavy}_{i}\beta_{8} \mbox{bcs}_{i}\mbox{gender}_{i}\beta_{9} + \mbox{pindex}_{i}\mbox{gender}_{i}\beta_{10} + \mbox{enzyme}_{i}\mbox{gender}_{i}\beta_{11} + \mbox{liver}_{i}\mbox{gender}_{i}\beta_{12} + \\ & \mbox{age}_{i}\mbox{gender}_{i}\beta_{13} + \mbox{bcs}_{i}\mbox{alc_mod}_{i}\beta_{14} + \mbox{pindex}_{i}\mbox{alc_mod}_{i}\beta_{15} + \mbox{enzyme}_{i}\mbox{alc_mod}_{i}\beta_{16} + \\ & \mbox{liver}_{i}\mbox{alc_mod}_{i}\beta_{17} + \mbox{age}_{i}\mbox{alc_mod}_{i}\beta_{18} + \mbox{bcs}_{i}\mbox{alc_heavy}_{i}\beta_{19} + \mbox{pindex}_{i}\mbox{alc_heavy}_{i}\beta_{20} + \\ & \mbox{enzyme}_{i}\mbox{alc_heavy}_{i}\beta_{21} + \mbox{liver}_{i}\mbox{alc_heavy}_{i}\beta_{22} + \mbox{age}_{i}\mbox{alc_heavy}_{i}\beta_{23} + \varepsilon_{i}. \end{split} \nonumber \end{equation}\] En este caso tenemos \(2^{23}=8'388,608\) posibles modelos. Lo que hace que sea difícil ajustarlos todos (aunque es posible usando la librería leaps). Por lo tanto, vamos a utilizar los algortimos de selección.

Selección hacia delante. Podemos utilizar la función ols_step_forward_aic de la librería olsrr:

mod.surgical.completo2 = lm(log.y~bcs*gender+pindex*gender+enzyme_test*gender+liver_test*gender+age*gender+ bcs*alc_mod+pindex*alc_mod+enzyme_test*alc_mod+liver_test*alc_mod+age*alc_mod+bcs*alc_heavy+pindex*alc_heavy+enzyme_test*alc_heavy+liver_test*alc_heavy+age*alc_heavy,data=surgical)
ols_step_forward_aic(mod.surgical.completo2,details = F)

## 
## 
##                                  Stepwise Summary                                  
## ---------------------------------------------------------------------------------
## Step    Variable                AIC       SBC        SBIC        R2       Adj. R2 
## ---------------------------------------------------------------------------------
##  0      Base Model             79.529    83.507     -77.331    0.00000    0.00000 
##  1      enzyme_test            51.434    57.401    -106.921    0.42725    0.41624 
##  2      pindex                 24.767    32.723    -134.607    0.66318    0.64997 
##  3      bcs:alc_heavy          -3.014     6.931    -162.432    0.80596    0.79432 
##  4      bcs                    -9.430     2.504    -169.458    0.83396    0.82041 
##  5      gender:pindex         -10.781     3.142    -171.655    0.84395    0.82770 
##  6      gender:enzyme_test    -19.676    -3.764    -180.194    0.87246    0.85618 
##  7      gender                -23.040    -5.139    -183.572    0.88452    0.86695 
##  8      age                   -24.081    -4.192    -184.830    0.89085    0.87144 
## ---------------------------------------------------------------------------------
## 
## Final Model Output 
## ------------------
## 
##                          Model Summary                          
## ---------------------------------------------------------------
## R                       0.944       RMSE                 0.161 
## R-Squared               0.891       MSE                  0.031 
## Adj. R-Squared          0.871       Coef. Var            2.741 
## Pred R-Squared          0.844       AIC                -24.081 
## MAE                     0.131       SBC                 -4.192 
## ---------------------------------------------------------------
##  RMSE: Root Mean Square Error 
##  MSE: Mean Square Error 
##  MAE: Mean Absolute Error 
##  AIC: Akaike Information Criteria 
##  SBC: Schwarz Bayesian Criteria 
## 
##                                ANOVA                                
## -------------------------------------------------------------------
##                Sum of                                              
##               Squares        DF    Mean Square      F         Sig. 
## -------------------------------------------------------------------
## Regression     11.407         8          1.426    45.909    0.0000 
## Residual        1.398        45          0.031                     
## Total          12.805        53                                    
## -------------------------------------------------------------------
## 
##                                       Parameter Estimates                                       
## -----------------------------------------------------------------------------------------------
##              model      Beta    Std. Error    Std. Beta      t        Sig      lower     upper 
## -----------------------------------------------------------------------------------------------
##        (Intercept)     3.949         0.238                 16.577    0.000     3.469     4.429 
##        enzyme_test     0.019         0.002        0.830    12.162    0.000     0.016     0.022 
##             pindex     0.011         0.002        0.383     4.903    0.000     0.007     0.016 
##                bcs     0.067         0.017        0.218     3.892    0.000     0.032     0.101 
##             gender     0.655         0.277        0.671     2.362    0.023     0.097     1.214 
##                age    -0.004         0.002       -0.081    -1.615    0.113    -0.008     0.001 
##      bcs:alc_heavy     0.052         0.010        0.288     5.234    0.000     0.032     0.073 
##      pindex:gender     0.003         0.003        0.198     0.914    0.366    -0.003     0.009 
## enzyme_test:gender    -0.010         0.002       -0.828    -4.002    0.000    -0.014    -0.005 
## -----------------------------------------------------------------------------------------------

Con el argumento details = T se puede ver la selección con más detalle. Usando este algoritmo el modelo óptimo es: \[\begin{equation} \begin{split} \log y_{i} =& \beta_{0} + \mbox{bcs}_{i}\beta_{1} + \mbox{pindex}_{i}\beta_{2} + \mbox{enzyme}_{i}\beta_{3} + \mbox{age}_{i}\beta_{4} + \mbox{gender}_{i}\beta_{5} + \\ &\mbox{gender}_{i}\mbox{pindex}_{i}\beta_{6} + \mbox{gender}_{i}\mbox{enzyme}_{i}\beta_{7} + \mbox{bcs}_{i}\mbox{alc_heavy}_{i}\beta_{8} + \varepsilon_{i}. \end{split} \nonumber \end{equation}\]

Selección hacia atrás. Podemos utilizar la función ols_step_backward_aic de la librería olsrr:

ols_step_backward_aic(mod.surgical.completo2,details = F)

## 
## 
##                                    Stepwise Summary                                    
## -------------------------------------------------------------------------------------
## Step    Variable                   AIC       SBC        SBIC         R2       Adj. R2 
## -------------------------------------------------------------------------------------
##  0      Full Model                -9.135    40.589     -172.353    0.91740    0.85408 
##  1      age:alc_heavy            -11.134    36.601     -173.941    0.91740    0.85878 
##  2      alc_heavy                -13.133    32.614      -45.421    0.91740    0.86319 
##  3      bcs:alc_mod              -15.057    28.701      -53.959    0.91728    0.86715 
##  4      age:alc_mod              -16.852    24.916      -62.617    0.91697    0.87057 
##  5      gender:pindex            -18.639    21.141    -1118.918    0.91664    0.87377 
##  6      alc_mod                  -19.980    17.811      -69.924    0.91562    0.87577 
##  7      enzyme_test:alc_heavy    -20.698    15.104      -79.945    0.91359    0.87622 
##  8      liver_test:alc_heavy     -20.988    12.824      -89.749    0.91081    0.87560 
##  9      pindex:alc_heavy         -22.223     9.601      -98.678    0.90954    0.87706 
##  10     pindex:alc_mod           -22.957     6.878     -107.457    0.90739    0.87729 
##  11     bcs:gender               -22.981     4.865     -164.788    0.90394    0.87583 
##  12     gender:age               -23.038     2.819     -108.929    0.90042    0.87434 
##  13     gender:liver_test        -23.549     0.319     -196.032    0.89764    0.87383 
##  14     age                      -23.745    -1.866     -183.861    0.89416    0.87251 
## -------------------------------------------------------------------------------------
## 
## Final Model Output 
## ------------------
## 
##                          Model Summary                          
## ---------------------------------------------------------------
## R                       0.946       RMSE                 0.158 
## R-Squared               0.894       MSE                  0.031 
## Adj. R-Squared          0.873       Coef. Var            2.729 
## Pred R-Squared          0.841       AIC                -23.745 
## MAE                     0.127       SBC                 -1.866 
## ---------------------------------------------------------------
##  RMSE: Root Mean Square Error 
##  MSE: Mean Square Error 
##  MAE: Mean Absolute Error 
##  AIC: Akaike Information Criteria 
##  SBC: Schwarz Bayesian Criteria 
## 
##                                ANOVA                                
## -------------------------------------------------------------------
##                Sum of                                              
##               Squares        DF    Mean Square      F         Sig. 
## -------------------------------------------------------------------
## Regression     11.449         9          1.272    41.302    0.0000 
## Residual        1.355        44          0.031                     
## Total          12.805        53                                    
## -------------------------------------------------------------------
## 
##                                       Parameter Estimates                                        
## ------------------------------------------------------------------------------------------------
##               model      Beta    Std. Error    Std. Beta      t        Sig      lower     upper 
## ------------------------------------------------------------------------------------------------
##         (Intercept)     3.568         0.220                 16.227    0.000     3.124     4.011 
##                 bcs     0.070         0.022        0.230     3.161    0.003     0.026     0.115 
##              gender     0.829         0.196        0.849     4.234    0.000     0.435     1.224 
##              pindex     0.014         0.002        0.475     7.952    0.000     0.010     0.017 
##         enzyme_test     0.022         0.002        0.947     9.262    0.000     0.017     0.027 
##          liver_test    -0.082         0.059       -0.178    -1.396    0.170    -0.200     0.036 
##  gender:enzyme_test    -0.009         0.002       -0.823    -3.894    0.000    -0.014    -0.005 
## enzyme_test:alc_mod    -0.004         0.002       -0.348    -2.156    0.037    -0.008     0.000 
##  liver_test:alc_mod     0.123         0.055        0.396     2.230    0.031     0.012     0.235 
##       bcs:alc_heavy     0.062         0.012        0.338     5.201    0.000     0.038     0.085 
## ------------------------------------------------------------------------------------------------

Por lo tanto, el modelo seleccionado es: \[\begin{equation} \begin{split} \log y_{i} =& \beta_{0} + \mbox{bcs}_{i}\beta_{1} + \mbox{pindex}_{i}\beta_{2} + \mbox{enzyme}_{i}\beta_{3} + \mbox{gender}_{i}\beta_{4} + \mbox{liver}_{i}\beta_{5} + \\ & \mbox{gender}_{i}\mbox{enzyme}_{i}\beta_{6} + \mbox{enzyme}_{i}\mbox{alc_mod}_{i}\beta_{7} + \mbox{liver}_{i}\mbox{alc_mod}_{i}\beta_{8} + \mbox{liver}_{i}\mbox{gender}_{i}\beta_{9} + \varepsilon_{i}. \end{split} \nonumber \end{equation}\] Con este algoritmo no se considera la edad del paciente pero si la función hepática y otras interacciones.

Selección por segmentos. Aquí tenemos la función ols_step_both_aic de la librería olsrr:

ols_step_both_aic(mod.surgical.completo2,details = F)

## 
## 
##                                    Stepwise Summary                                    
## -------------------------------------------------------------------------------------
## Step    Variable                    AIC       SBC        SBIC        R2       Adj. R2 
## -------------------------------------------------------------------------------------
##  0      Base Model                 79.529    83.507     -77.331    0.00000    0.00000 
##  1      enzyme_test (+)            51.434    57.401    -106.921    0.42725    0.41624 
##  2      pindex (+)                 24.767    32.723    -134.607    0.66318    0.64997 
##  3      bcs:alc_heavy (+)          -3.014     6.931    -162.432    0.80596    0.79432 
##  4      bcs (+)                    -9.430     2.504    -169.458    0.83396    0.82041 
##  5      gender:pindex (+)         -10.781     3.142    -171.655    0.84395    0.82770 
##  6      gender:enzyme_test (+)    -19.676    -3.764    -180.194    0.87246    0.85618 
##  7      gender (+)                -23.040    -5.139    -183.572    0.88452    0.86695 
##  8      gender:pindex (-)         -23.631    -7.719    -183.529    0.88147    0.86634 
##  9      age (+)                   -25.088    -7.187    -185.232    0.88882    0.87190 
## -------------------------------------------------------------------------------------
## 
## Final Model Output 
## ------------------
## 
##                          Model Summary                          
## ---------------------------------------------------------------
## R                       0.943       RMSE                 0.162 
## R-Squared               0.889       MSE                  0.031 
## Adj. R-Squared          0.872       Coef. Var            2.736 
## Pred R-Squared          0.846       AIC                -25.088 
## MAE                     0.131       SBC                 -7.187 
## ---------------------------------------------------------------
##  RMSE: Root Mean Square Error 
##  MSE: Mean Square Error 
##  MAE: Mean Absolute Error 
##  AIC: Akaike Information Criteria 
##  SBC: Schwarz Bayesian Criteria 
## 
##                                ANOVA                                
## -------------------------------------------------------------------
##                Sum of                                              
##               Squares        DF    Mean Square      F         Sig. 
## -------------------------------------------------------------------
## Regression     11.381         7          1.626    52.535    0.0000 
## Residual        1.424        46          0.031                     
## Total          12.805        53                                    
## -------------------------------------------------------------------
## 
##                                       Parameter Estimates                                       
## -----------------------------------------------------------------------------------------------
##              model      Beta    Std. Error    Std. Beta      t        Sig      lower     upper 
## -----------------------------------------------------------------------------------------------
##        (Intercept)     3.864         0.219                 17.667    0.000     3.423     4.304 
##        enzyme_test     0.019         0.002        0.828    12.157    0.000     0.016     0.022 
##             pindex     0.013         0.001        0.437     8.697    0.000     0.010     0.016 
##                bcs     0.067         0.017        0.220     3.946    0.000     0.033     0.102 
##             gender     0.839         0.191        0.859     4.381    0.000     0.453     1.224 
##                age    -0.004         0.002       -0.086    -1.744    0.088    -0.008     0.001 
##      bcs:alc_heavy     0.054         0.010        0.294     5.392    0.000     0.034     0.074 
## enzyme_test:gender    -0.010         0.002       -0.838    -4.063    0.000    -0.014    -0.005 
## -----------------------------------------------------------------------------------------------

Note que este método sigue los mismos pasos que la selección hacia delante hasta el paso 8 donde se elimina la interacción entre el índice de pronostico y el genero. Por lo que aquí obtenemos el siguiente modelo:

\[\begin{equation} \begin{split} \log y_{i} =& \beta_{0} + \mbox{bcs}_{i}\beta_{1} + \mbox{pindex}_{i}\beta_{2} + \mbox{enzyme}_{i}\beta_{3} + \mbox{age}_{i}\beta_{4} + \mbox{gender}_{i}\beta_{5} + \\ & \mbox{gender}_{i}\mbox{enzyme}_{i}\beta_{6} + \mbox{bcs}_{i}\mbox{alc_heavy}_{i}\beta_{7} + \varepsilon_{i}. \end{split} \nonumber \end{equation}\]

Dado que los algoritmos hacen la busqueda del modelo “óptimo” evaluando diferentes subconjuntos de covariables, se obtuvieron diferentes ajustes. Si observamos el AIC de las tres opciones, el modelo obtenido con el algoritmo stepwise presenta el mejor resultado.

4.5 Regresión de LASSO

Otra alternativa para encontrar las variables relevantes es a través del estimador de LASSO (Least Absolute Selection and Shrinkage Operator). Este es un método de regularización que se implementa se tiene cientos de covariables disponibles y se cree que pocas tienen un aporte relevante (sparsity principle). Por ejemplo, en estudios de genética se tienen miles de genes disponibles pero solo unos pocos son activos para una mutación de interés.

Aquí se asume el modelo de regresión usual, donde: \[ E(y | \boldsymbol x) = \boldsymbol x'\boldsymbol \beta, \mbox{ y } V(y | \boldsymbol x) = \sigma^2, \] pero muchos de los elementos de \(\boldsymbol \beta\) son iguales a cero. El objetivo del estimador de LASSO seleccionar los coeficientes que tienen valores diferentes de cero. Esto se obtiene minimizando la siguiente expresión:

\[\begin{equation} S_{lasso}(\beta)= \sum_{i=1}^{n}(y_{i}-x_{i}'\boldsymbol \beta)^{2}+ \lambda\sum_{j=1}^{p-1}|\beta_{j}|, \tag{4.3} \end{equation}\] con \(\lambda \geq 0\). Note que (4.3) es la suma de cuadrados del estimador por MCO más una penalización (dada por \(\lambda\)) a la suma del valor absoluto de los coeficientes (exceptuando el intercepto). Si \(\lambda=0\), se obtiene el estimador por MCO. A medida que \(\lambda\) aumenta la penalización tendrá mas peso sobre la estimación de los coeficientes. Por lo que si este parámetro es suficientemente grande, todas las estimaciones serán iguales a cero (con excepción del intercepto). También se puede probar que, cuando \(\lambda \rightarrow \infty\), la varianza de \(\widehat{\boldsymbol \beta}_{LASSO}\) disminuye, pero el sesgo aumenta.

De forma de equivalente, el estimador de LASSO minimiza:

\[ \sum_{i=1}^{n}(y_{i}-x_{i}^{′}\boldsymbol \beta)^{2} \quad \mbox{ sujeto a } \quad \sum_{j=1}^{p-1}|\beta_{j} | \leq t. \]

Mientras que, en la regresión de ridge minimiza:

\[ \sum_{i=1}^{n}(y_{i}-x_{i}^{′}\boldsymbol \beta)^{2} \quad \mbox{ sujeto a } \quad \sum_{j=1}^{p-1}\beta_{j}^2\leq t. \]

La Figura 4.3 muestra como intervienen las restricciones del estimador de LASSO (izquierda) y ridge (derecha) en un modelo con dos covariables. Los contornos muestras la suma de cuadrado de los errores, mientras que, las restricciones están dadas por el diamante \((|\beta_1|+|\beta_2| \leq t)\) y la circunferencia \((\beta_1^2+\beta_2^2 \leq t)\) rojas para el estimador LASSO y ridge, respectivamente. La solución de ambos estimadores se encuentra en el punto donde el contorno elíptico intercepta la región de la restricción. Para la regresión LASSO, si la solución ocurre en una esquina, entonces la estimación del parámetro es igual a cero.

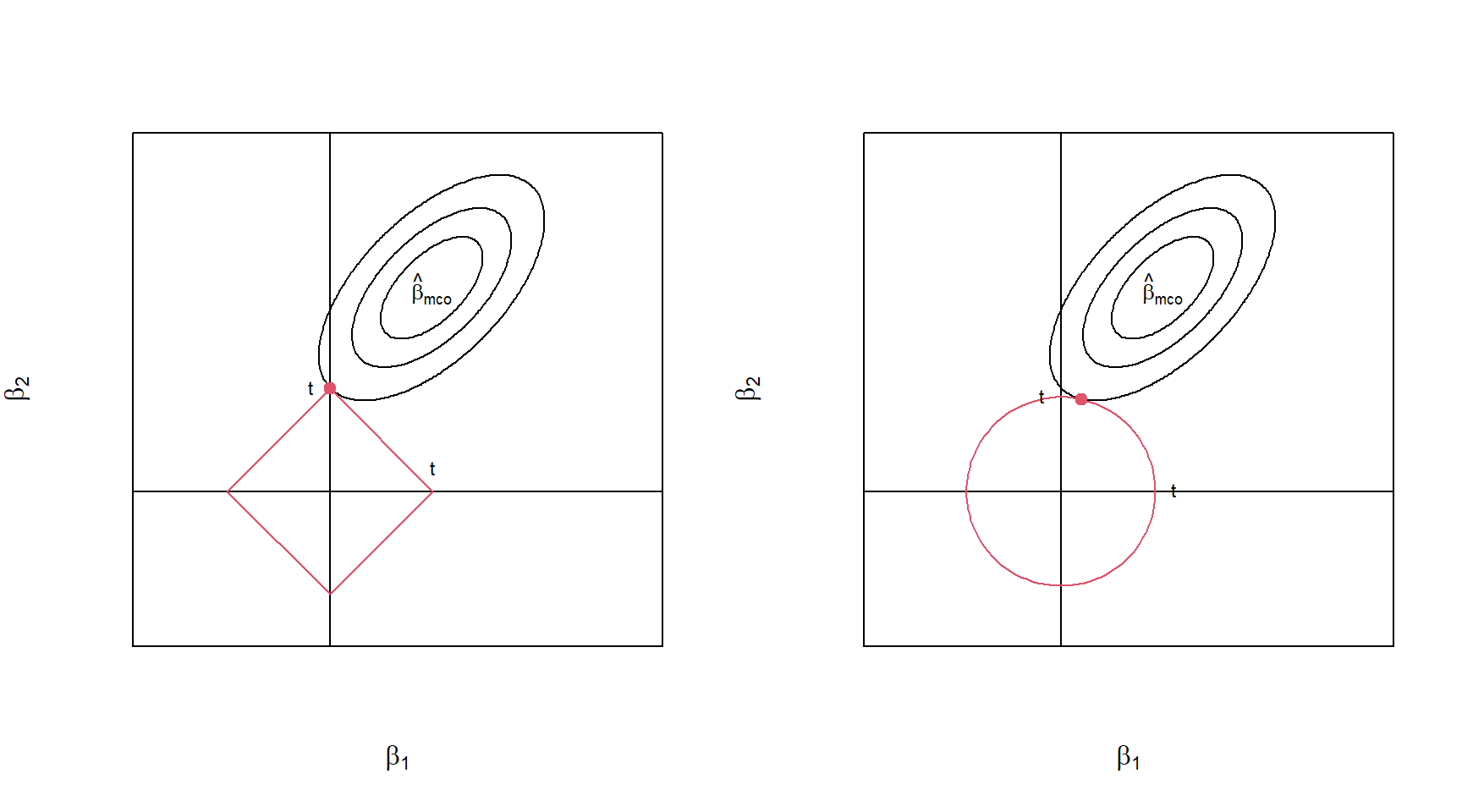
Figure 4.3: Estimación del estimador de LASSO (izquierda) y ridge (derecha). Las elipses rojas son los contornos de la suma de cuadrados de los errores. Mientras que, la región roja son las restricciones para cada estimador).

Dado que (4.3) es una función no lineal en \(y\), no hay solución analítica para \(\widehat{\boldsymbol \beta}_{LASSO}\). Sin embargo, pero hay algoritmos eficientes para su estimación. De igual forma, se recomienda escalar las variables para remover el efecto de las unidades de medida.

En R, la estimación del modelo por medio del estimador de LASSO se hace por medio de la función glmnet de la librería glmnet.

4.5.1 Datos de grasa corporal

La estimación de los coeficientes de regresión del modelo (4.1) por medio del estimador de LASSO para diferentes valores de \(\lambda\) se puede observar en la Figura 4.4. Se puede observar que a medida que \(\lambda\) aumenta, mas coeficientes de regresión son iguales a cero.

#se debe especificar alpha=1
X = model.matrix(mod.fat)[,-1]
lasso.mod <- glmnet(X, fat$brozek, alpha = 1,nlambda = 100)
plot(lasso.mod,xvar='lambda',label=T,lwd=2,ylab='coeficientes de regresión')
abline(h=0,lty=2)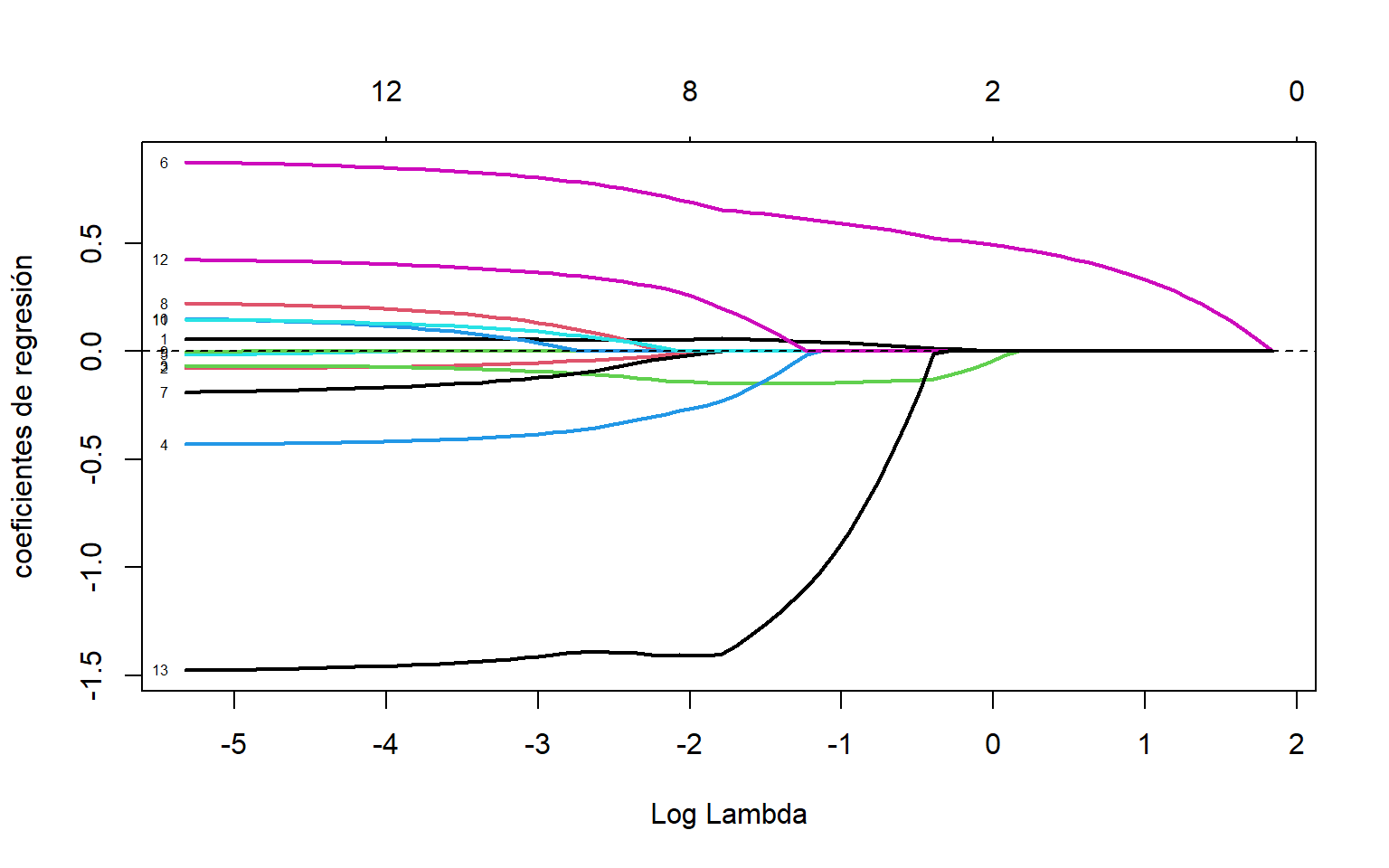

Figure 4.4: Datos de grasa corporal. Estimación de los coeficientes de regresión vs el logaritmo de \(\lambda\)

La pregunta sería que valor de \(\lambda\) se debe seleccionar para determinar los coeficientes que son diferentes de cero. Una alternativa que tenemos para ello es por medio de validación cruzada.

4.5.2 Validación cruzada

La validación cruzada (CV) es un método general para evaluar que tan bueno es un modelo para predecir observaciones futuras de la población objetivo del estudio. La idea es dividir la muestra en dos grupos:

• (1) Entrenamiento: se usa para ajusta el modelo.
• (2) Validación: se utiliza para validar el modelo ajustado.

Para no perder información, en la CV se realiza en \(K\) iteraciones dividiendo los datos en \(K\) subconjuntos. En cada iteración, uno de los subconjutos es utilizado como datos de validación y el resto de subgrupos \((K-1)\) como datos de entrenamiento.

Para cada división,\(k = 1, . . . , K\), y para cada valor de \(\lambda\), se estima el modelo basado en la muestra de entrenamiento. Mientras que con cada muestra de validación, y para cada valor de \(\lambda\), se utiliza para calcular el error cuadrático medio:

\[ EMC_{k}(\lambda) = \sum_{i=1}^{n_k} \frac{[y_{i}^{(k)}-\boldsymbol x_{i}^{(k)}\widehat{\boldsymbol \beta}_{lasso}^{(k)}(\lambda)]^2}{n} \]

donde \(y_{i}^{(k)}\) son las observaciones de la muestra de validación \(k\), y \(\widehat{\boldsymbol \beta}_{lasso}^{(k)}(\lambda)\) es la estimación utilizando la muestra de entrenamiento \(k\). Finalmente, para cada \(\lambda\), se calcula: \[ CV(\lambda) = \frac{1}{K}\sum_{i=1}^{K}EMC_{k}(\lambda) \] y la desviación estándar: \[ SD(\lambda) = \sqrt{\sum_{i=1}^{K} \frac{[EMC_{k}(\lambda)-CV(\lambda)]^2}{K-1}} \] Luego, el valor de \(\lambda\) seleccionado corresponde al valor que minimiza \(CV(\lambda)\): \[ \hat{\lambda}_{cv}=arg\quad mín_{\lambda}-CV(\lambda) \] También, se puede aplicar la regla de una desviación estándar:

\[ \hat{\lambda}_{cv1sd}=máx \{\lambda:CV(\hat{\lambda})<CV(\hat{\lambda}_{cv})+SD(\hat{\lambda}_{cv})\} \] El segundo método es preferible dado que tiene en cuenta la variabilidad debida a la selección de las submuestras.

4.5.3 Ejemplo grasa corporal

La estimación de \(\lambda\) por medio de CV se puede hacer con la función cv.glmnet determinando del número de subconjuntos con el argumento nfolds. Por ejemplo, si consideramos \(K=10\), se obtienen los siguientes resultados:

set.seed(123)
lasso.cv <-cv.glmnet(X, fat$brozek, nfolds = 10, alpha = 1,nlambda = 100)
plot(lasso.cv)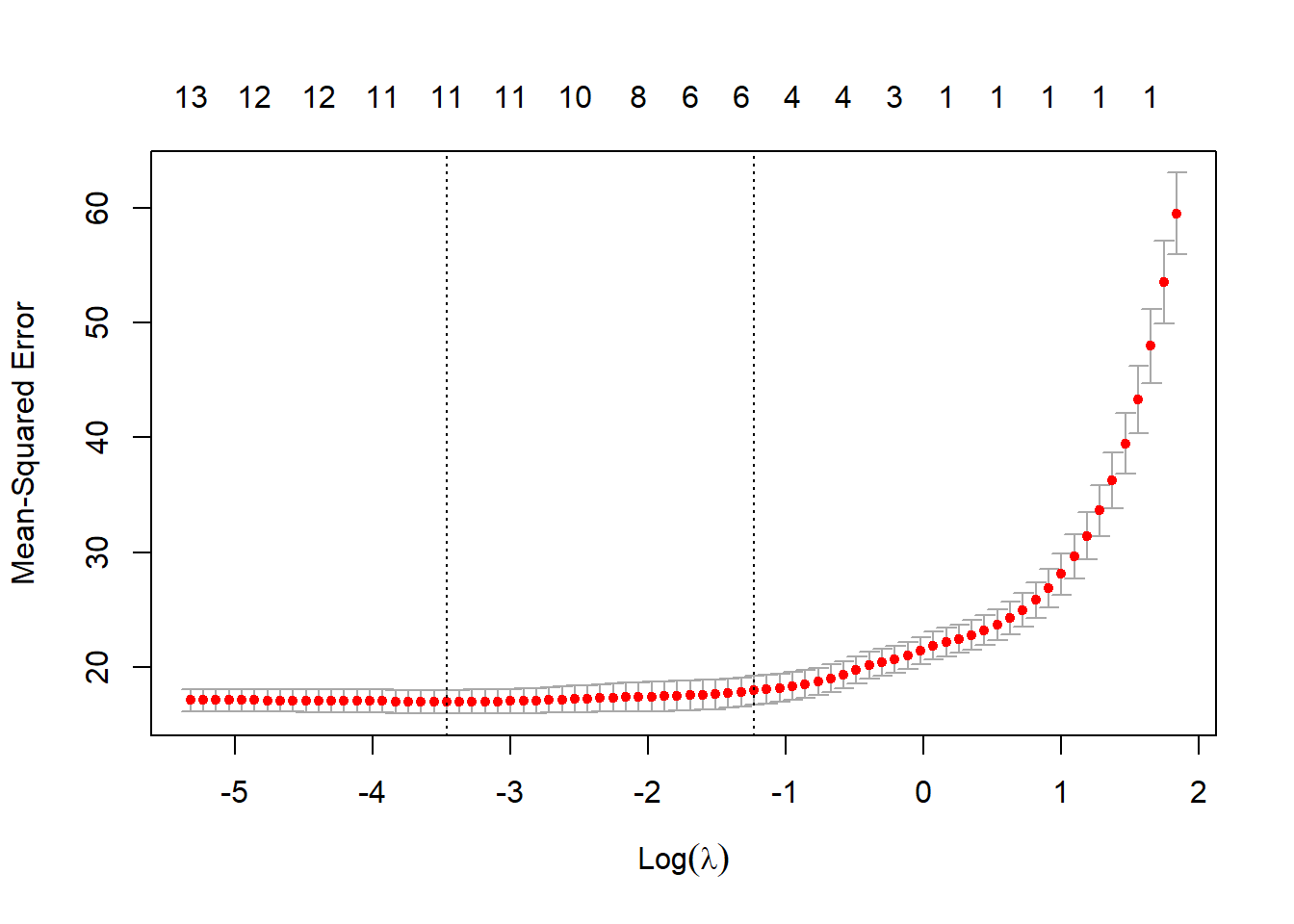

Figure 4.5: Datos de grasa corporal. Valiación cruzada (puntos rojos) para diferentes valores de \(\lambda\). Las lineas cortadas verticales representan los valores seleccionados para \(\lambda\) por mínimo valores de CV y la regla de una desviación estándar.

Las covariables seleccionadas al utlizar el estimador de LASSO con el \(\lambda\) óptimo (regla una desviación estándar) son:

est = glmnet(X, fat$brozek, alpha = 1,lambda = lasso.cv$lambda.1se)
est$beta

## 13 x 1 sparse Matrix of class "dgCMatrix"
##                  s0
## age      0.04428910
## weight   .         
## height  -0.14861287
## neck    -0.01394232
## chest    .         
## abdom    0.61111812
## hip      .         
## thigh    .         
## knee     .         
## ankle    .         
## biceps   .         
## forearm  .         
## wrist   -1.08873009

La selección de variables por medio del estimador LASSO son age, height, neck,abdom y wrist. Ahora ajustamos el modelo con estas variables por medio de MCO:

mod.lasso = lm(brozek ~ age+height+neck+abdom+wrist,data=fat)
summary(mod.lasso)

## 
## Call:
## lm(formula = brozek ~ age + height + neck + abdom + wrist, data = fat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -14.9618  -2.9130  -0.1425   2.9188  10.1956 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  2.23156    6.31879   0.353  0.72427    
## age          0.06064    0.02206   2.749  0.00642 ** 
## height      -0.15037    0.07806  -1.926  0.05520 .  
## neck        -0.39169    0.19570  -2.002  0.04644 *  
## abdom        0.71970    0.03802  18.931  < 2e-16 ***
## wrist       -1.49192    0.44127  -3.381  0.00084 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.093 on 246 degrees of freedom
## Multiple R-squared:  0.7267, Adjusted R-squared:  0.7212 
## F-statistic: 130.8 on 5 and 246 DF,  p-value: < 2.2e-16

Las covariables selecciondas en este modelo son todas significativas, a excepción de la circunferencia del cuello. Además, \(R^2=0.7267\) y \(R^2_{adj}=0.7178\). Comparado con el modelo completo, estás cantidades han disminuido ligeramente.

La Tabla 4.1 muestra las estimaciones de los modelos ajustados utilizando diferentes métodos de selección de variables. En los tres modelos coinciden con la inclusión de la circunferencia del abdomen y de la muñeca. Las variables peso y estatura se encuentran en algunos de estos modelos, pero no de forma simultanea. Esto sugiere que proporcionan la misma información y no es necesario incluirlas juntas. Finalmente, se puede observar en la Tabla 4.2 que los tres modelos proporcionan similar ajuste.

Table 4.1: datos de grasa corporal. Estimación de coeficientes de los modelos seleccionados

Método de selección
	AIC y PRESS			BIC			LASSO
	Est	er. std.	valor-p	Est	er. std.	valor-p	Est	er. std.	valor-p
int.	-20.062	10.8465	0.0656	-31.297	6.7089	0.0000	2.234	6.3188	0.7243
age	0.059	0.0285	0.0388				0.061	0.0221	0.0064
weight	-0.084	0.037	0.0237	0.126	0.0229	0.0000
height							-0.15	0.0781	0.0552
neck	-0.432	0.208	0.0389				-0.392	0.1957	0.0464
abdom	0.877	0.0666	0.0000	0.921	0.0519	0.0000	0.72	0.038	0.0000
hip	-0.186	0.1282	0.1473
thigh	0.286	0.1195	0.1473
forearm	0.4825	0.1725	0.0056	0.446	0.1682	0.0085
wrist	-1.4049	0.4717	0.0032	-1.392	0.4099	8e-04	-1.492	0.4413	0.0000

Table 4.2: datos de grasa corporal. Valores de los criterios de selección para los modelos seleccionados.

Modelo	\(R^2\)	PRESS	AIC	BIC
AIC y PRESS	0.7467	4139.682	1420.225	1455.520
BIC	0.7351	4209.140	1423.471	1444.647
LASSO	0.7267	4416.440	1433.318	1458.024

La selección del modelo más adecuado no solo debe depender de un análisis estadístico, sino también de la opinión de expertos en el tema.