Capítulo 3 Multicolinealidad
3.1 Ejemplos
3.1.1 Cemento
Los datos data(cement), de la librería MASS, corresponden a un experimento para evaluar el efecto de diferentes combinaciones químicas sobre el calor emanado en el fraguado del cemento Portland. Para esto, se tiene una muestra de \(13\) fraguados de cemento. En cada muestra, se midió con precisión los porcentajes de los cuatro ingredientes químicos principales (covariables). Mientras el cemento fraguaba, también se midió la cantidad de calor desprendido (cals/gm, variable respuesta). Los cuatro ingredientes químicos son: x1 aluminato tricálcico (%), x2 silicato tricálcico (%), x3 tetra-aluminio ferrita de calcio (%), y x4 silicato dicálcico (%).
En la Figura 3.1 podemos observar que hay relaciones lineales positivas entre la variable respuesta y las covariables aluminato tricálcico y silicato tricálcico. Mientras que la relación con la variable silicato dicálcico es negativa. También podemos notar que hay una relación negativa fuerte en las covariables aluminato tricálcico y tetra-aluminio ferrita de calcio, y entre silicato tricálcico y silicato dicálcico.
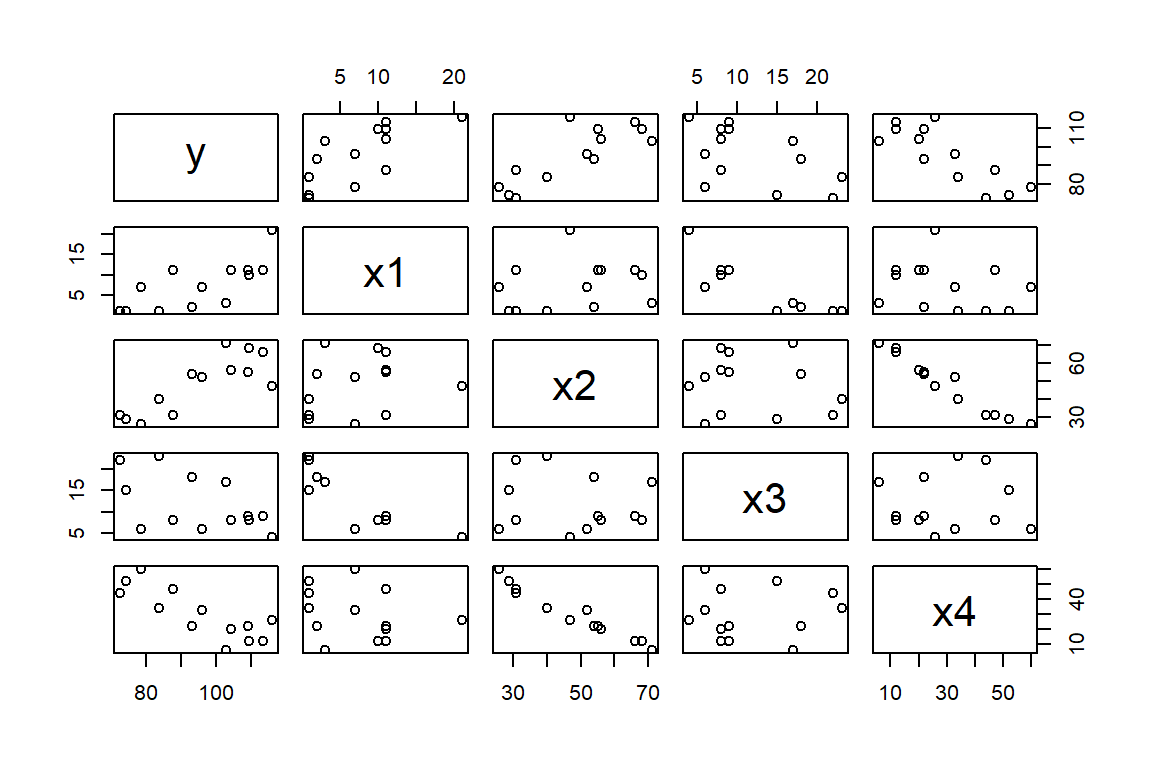
Figure 3.1: Datos de cemento. Diagrama de dispersión de las variables.
Para estos datos, se propone el siguiente modelo: \[ y_{i} = \beta_{0} + x_{1i}\beta_{1} + x_{2i}\beta_{2} + x_{3i}\beta_{3} + x_{4i}\beta_{4} + \varepsilon_{i}, \] donde \(\varepsilon_{i} \sim N(0, \sigma^2)\) y \(cov(\varepsilon_{i},\varepsilon_{j})=0\) para todo \(i \neq j\).
Los resultados del ajuste son:
##
## Call:
## lm(formula = y ~ x1 + x2 + x3 + x4, data = cement)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.1750 -1.6709 0.2508 1.3783 3.9254
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 62.4054 70.0710 0.891 0.3991
## x1 1.5511 0.7448 2.083 0.0708 .
## x2 0.5102 0.7238 0.705 0.5009
## x3 0.1019 0.7547 0.135 0.8959
## x4 -0.1441 0.7091 -0.203 0.8441
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.446 on 8 degrees of freedom
## Multiple R-squared: 0.9824, Adjusted R-squared: 0.9736
## F-statistic: 111.5 on 4 and 8 DF, p-value: 4.756e-07Estos resultados suguieren que el ajuste es muy bueno, el \(98.2\)% de la variabilidad de la cantidad de calor desprendido durante la fraguado es explicada por el modelo. Sin embargo, los resultados de las pruebas de hipótesis individuales sobre los coeficientes muestran valores \(p\) muy grandes. Estos resultados parecen contradictorios.
3.1.2 Grasa corporal
Se tiene una muestra de \(20\) mujeres saludables con edades entre \(25\) y \(34\) años (data(bodyfat) en la librería isdals). La medición del porcentaje de grasa corporal es caro y engorroso, por lo tanto se quiere buscar un modelo que proporcione predicciones fiables. Como variables de este modelo se utiliza: Triceps: pliegue cutáneo del tríceps (cm), Thigh: circunferencia del muslo (cm), y Midarm: circunferencia del brazo medio (cm).
La Figura 3.2 muestra la relación entre variables. Podemos observar que hay una relación fuerte del % de masa corporal con el pliegue cutáneo del triceps y la circunferencia del brazo medio. Además, hay una relación lineal fuerte entre esas dos covariables.
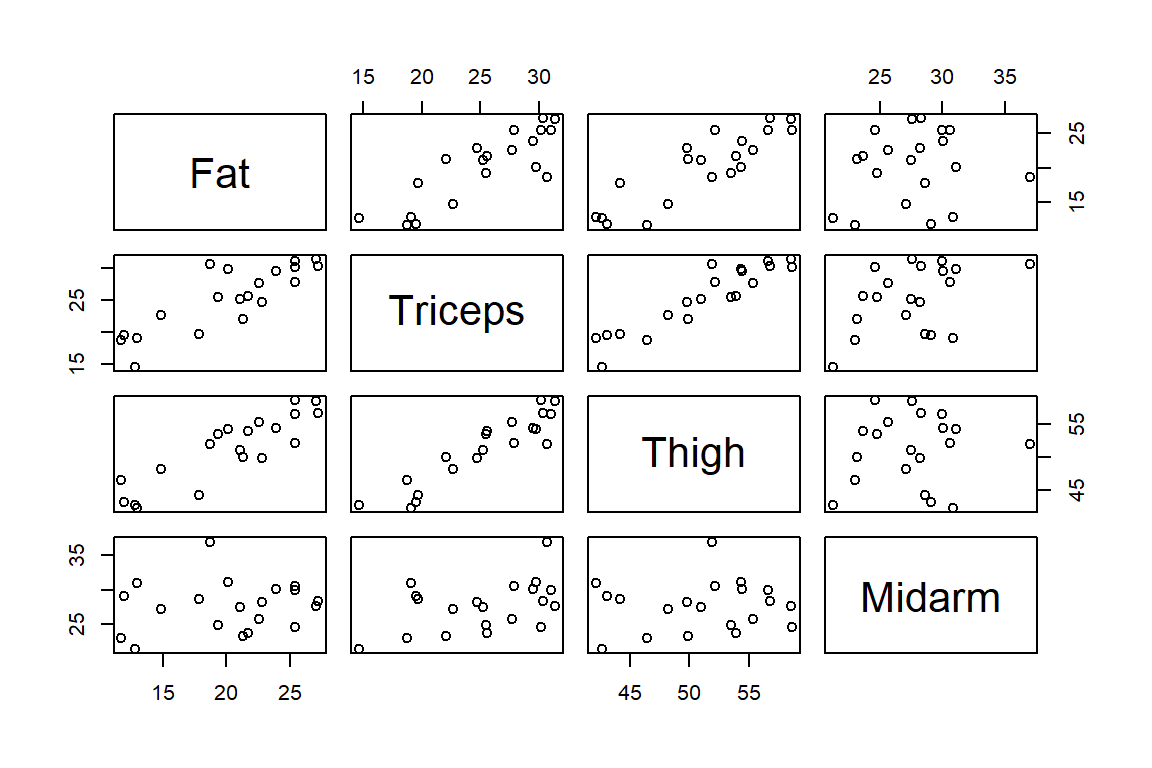
Figure 3.2: Datos de grasa corporal. Diagrama de dispersión de las variables.
El modelo propuesto es: \[ \mbox{Fat}_{i} = \beta_{0} + \mbox{Triceps}_{i}\beta_{1} + \mbox{Thigh}_{i}\beta_{2} + \mbox{Midarm}_{i}\beta_{3} + \varepsilon_{i}, \] donde \(\varepsilon_{i} \sim N(0, \sigma^2)\) y \(cov(\varepsilon_{i},\varepsilon_{j})=0\) para todo \(i \neq j\).
El ajuste del modelo es el siguiente:
##
## Call:
## lm(formula = Fat ~ Triceps + Thigh + Midarm, data = bodyfat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.7263 -1.6111 0.3923 1.4656 4.1277
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 117.085 99.782 1.173 0.258
## Triceps 4.334 3.016 1.437 0.170
## Thigh -2.857 2.582 -1.106 0.285
## Midarm -2.186 1.595 -1.370 0.190
##
## Residual standard error: 2.48 on 16 degrees of freedom
## Multiple R-squared: 0.8014, Adjusted R-squared: 0.7641
## F-statistic: 21.52 on 3 and 16 DF, p-value: 7.343e-06Así como en el caso anterior, observamos que el modelo explica gran parte de la variabilidad del % de grasa corporal. Sin embargo, los valores \(p\) de las pruebas individuales sobre los coeficientes son altos.
3.2 Multicolinealidad
Para el modelo: \[ \boldsymbol y= \boldsymbol X\boldsymbol \beta+ \boldsymbol \varepsilon, \mbox{ con } \boldsymbol \varepsilon\sim N(\boldsymbol 0, \sigma^2 \boldsymbol I), \] el estimador de \(\boldsymbol \beta\) es \(\widehat{\boldsymbol \beta}= (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y\). Además, se tiene que \(V(\widehat{\boldsymbol \beta}) = \sigma^{2}(\boldsymbol X'\boldsymbol X)^{-1}\). Por lo tanto, se requiere que \(\boldsymbol X\) sea de rango completo. Es decir, que no hayan columnas que sean linealmente dependientes. En algunos casos, las columnas de \(\boldsymbol X\) son casi linealmente dependientes o colineales,lo que lleva a que \(\boldsymbol X'\boldsymbol X\) sea casi singular, lo que puede provocar problemas a la hora de hacer inferencias.
Sea \(\boldsymbol x_j\) la \(j\)-ésima columna de la matriz \(\boldsymbol X\), por lo tanto \(\boldsymbol X= (\boldsymbol 1,\boldsymbol x_{1},\ldots,\boldsymbol x_{p-1})\). Los vectores \(\boldsymbol x_{1},\boldsymbol x_{2},\ldots,\boldsymbol x_{p-1}\) son linealmente dependientes si hay conjunto de constantes \(a_{1},a_{2},\ldots, a_{p-1}\) no todas igual a cero, tal que: \[ \sum_{j=1}^{p-1}a_{j}\boldsymbol x_{j} = c, \mbox{ donde }c\mbox{ es una constante.} \] Si esto se cumple, el rango de la matriz \(\boldsymbol X'\boldsymbol X\) es menor que \(p\), y por lo tanto, \((\boldsymbol X'\boldsymbol X)^{-1}\) no existe. Si la relación es aproximada \((\sum_{j=1}^{p-1}a_{j}\boldsymbol x_{j} \approx c)\), existe el problema de multicolinealidad.
Vamos a ilustrar el efecto de la multicolinealidad con un ejemplo sencillo. Consideremos un modelo lineal con dos covariables: \[ y_{i}^{*} = z_{i1}\beta_1 +z_{i2}\beta_2 +\varepsilon_i, \] donde las covariables están escaladas con longitud unitaria. Esto es: \[ y_{i}^{*} = \frac{y_{i}-\bar{y}}{\sqrt{SST}}, \mbox{ y } z_{ij} = \frac{x_{ij} - \bar{x}_{j}}{\sqrt{s_{jj}}}, \] donde \(s_{jj} = \sum_{i=1}^{n}(x_{ij}-\bar{x}_{j})^{2}\). Además, sea \(\boldsymbol Z\) la matriz de covariables. Con esta transformación, tenemos que \(\boldsymbol Z'\boldsymbol Z\) es la matriz de correlación de las covariables, \[ \boldsymbol Z'\boldsymbol Z= \begin{pmatrix} 1 & r_{12} \\ r_{12} & 1 \end{pmatrix}, \] y \(\boldsymbol Z'\boldsymbol y\) es el vector de correlaciones entre \(y\) y las dos covariables: \[ \boldsymbol Z'\boldsymbol y^{*} = \begin{pmatrix} r_{y1} \\ r_{y2} \end{pmatrix}. \] Por lo que el estimador por MCO de \(\boldsymbol b\) está dado por: \[ \widehat{\boldsymbol b}= \begin{pmatrix} 1 & r_{12} \\ r_{12} & 1 \end{pmatrix}^{-1}\begin{pmatrix} r_{y1} \\ r_{y2} \end{pmatrix} = \begin{pmatrix} \frac{1}{1-r_{12}^{2}} & \frac{-r_{12}}{1-r_{12}^{2}} \\ \frac{-r_{12}}{1-r_{12}^{2}} & \frac{1}{1-r_{12}^{2}} \end{pmatrix} \begin{pmatrix} r_{1y} \\ r_{2y} \end{pmatrix}. \] Particularmente, tenemos que: \[ \widehat{b}_{1} = \frac{r_{1y}-r_{12}r_{2y}}{1-r_{12}^{2}} \mbox{ y } \widehat{b}_{2} = \frac{r_{2y}-r_{12}r_{1y}}{1-r_{12}^{2}}. \] Además, la matriz de varianzas-covarianzas de \(\widehat{\boldsymbol b}\) es: \[\begin{equation} V(\widehat{\boldsymbol b}) = \sigma^{2} \begin{pmatrix} \frac{1}{1-r_{12}^{2}} & \frac{-r_{12}}{1-r_{12}^{2}} \\ \frac{-r_{12}}{1-r_{12}^{2}} & \frac{1}{1-r_{12}^{2}} \end{pmatrix}. \tag{3.1} \end{equation}\] En (3.1) podemos observar que la varianza de los coeficientes \(\widehat{\boldsymbol b}\) tienden a infinito cuando \(|r_{12}|\rightarrow 1\). Mientras que se hace mínima cuando las covariables están incorrelacionadas \((r_{12}=0)\). Es decir, una fuerte correlación entre \(x_1\) y \(x_2\) da como resultado grandes varianzas y covarianzas para los coeficientes \(\widehat{\boldsymbol b}\).
Por esta razón es preferible tener covariables que sean ortogonales. Puesto que así se garantiza la menor varianza posible para \(\widehat{\boldsymbol \beta}\). Sin embargo, las covariables son díficiles de controlar en estudios observacionales.
Ahora consideremos un modelo con \(p-1\) covariables, \[ y_{i}^{*} = b_{1}z_{i1} + b_{2}z_{i2} + \ldots + b_{p-1}z_{i,p-1} + \varepsilon_{i}. \] Las ecuaciones normales son: \[ \begin{pmatrix} 1 & r_{12} & r_{13} & \ldots & r_{1,p-1} \\ r_{12} & 1 & r_{23} & \ldots & r_{2,p-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ r_{1,p-1} & r_{2,p-1} & r_{3,p-1} & \ldots & 1 \end{pmatrix} \begin{pmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{p-1} \end{pmatrix} = \begin{pmatrix} r_{y1} \\ r_{y2} \\ \vdots \\ r_{y,p-1} \end{pmatrix}. \] Por lo que el estimador de \(\boldsymbol b\) es: \[ \widehat{\boldsymbol b}= \boldsymbol R^{-1}\boldsymbol Z'\boldsymbol y^{*}, \mbox{donde }\boldsymbol R= \boldsymbol Z'\boldsymbol Z. \] La Varianza de \(\widehat{\boldsymbol b}\) está determinada por: \[ V(\widehat{\boldsymbol b})=\sigma^{2}\boldsymbol R^{-1} = \sigma^{2} \begin{pmatrix} 1 & \boldsymbol r' \\ \boldsymbol r& \boldsymbol R_{22}, \end{pmatrix}^{-1}, \] donde \(\boldsymbol r= (r_{12},r_{13},\ldots,r_{1,p-1})\) y \(\boldsymbol R_{22}\) es la matriz \(\boldsymbol R\) eliminando la primer fila y columna. Particularmente para \(\widehat{b}_1\), tenemos que: \[ V(\widehat{b}_1) = \sigma^{2}\frac{1}{1 - \boldsymbol r'\boldsymbol R_{22}^{-1}\boldsymbol r}. \]
Ahora asumamos que hacemos una regresión de \(Z_1\) en función de los demás regresores. Esto es: \[\begin{equation} z_1 = \alpha_1 z_2 + \alpha_2 z_3 + \ldots + \alpha_{p-2} z_{p-1}+\varepsilon_1. \tag{3.2} \end{equation}\] Las sumas de cuadrados totales y de los residuos de este modelo son: \[ SST = \sum_{i=1}^{n}z_{1i}^2 = 1, \] y \[ SS_{\mbox{res}}= SST - SS_{\mbox{reg}}= 1 - \boldsymbol z_1' \boldsymbol Z_{(1)}(\boldsymbol Z_{(1)}'\boldsymbol Z_{(1)})^{-1}\boldsymbol Z_{(1)}'\boldsymbol z_1= 1 - \boldsymbol r'R_{22}^{-1}\boldsymbol r, \] respectivamente, donde \(\boldsymbol Z_{(1)}\) es la matriz \(\boldsymbol Z\) sin la primer columna. Además, el coeficiente de determinación de (3.1) es: \[ R^{2}_1 = 1 - \frac{SS_{\mbox{res}}}{SS_{\mbox{T}}} = \boldsymbol r'R_{22}^{-1}\boldsymbol r. \] De aquí obtenemos que: \[ V(\widehat{b}_1) = \sigma^{2} \frac{1}{1-R^{2}_1}. \] De forma similar se puede demostrar que: \[ V(\widehat{b}_j) = \sigma^{2} \frac{1}{1-R^{2}_j}, j=1,\ldots,p-1, \] donde \(R^{2}_{j}\) es el coeficiente de determinación de la regresión de \(z_{j}\) en función de las \((p-2)\) covariables restantes. Por lo que, si \(R^{2}_{j} \rightarrow 1\), entonces \(V(\widehat{b}_{j})\rightarrow \infty\).
La multicolinealidad también produce que los estimadores \(\widehat{b}_{j}\) sean muy grandes en valor absoluto. Para verificar esto considere: \[ L_{1}^{2} = \sum_{j=1}^{p}(\widehat{b}_{j}-b_{j})^{2} = (\widehat{\boldsymbol b}- \boldsymbol b)'(\widehat{\boldsymbol b}- \boldsymbol b). \] El valor esperado de \(L_{1}^{2}\) es: \[ E(L_{1}^{2}) = E[ (\widehat{\boldsymbol b}- \boldsymbol b)'(\widehat{\boldsymbol b}- \boldsymbol b) ] = \sum_{j=1}^{p-1}\sigma^{2}\mbox{tr}\boldsymbol R^{-1} \] Dado que la traza de una matriz es igual a la suma de sus valores propios, tenemos que: \[ E(L_{1}^{2}) = \sigma^{2}\sum_{j=1}^{p-1}1/\lambda_{j}, \] donde \(\lambda_{j} > 0\), para \(j=1,\ldots,p-1\), son los valores propios de \(\boldsymbol R\). Por lo tanto, si \(\boldsymbol R\) está mal condicionada debido a la multicolinealidad, al menos un \(\lambda_{j}\) será muy pequeño.
Cabe notar que, el problema de multicolinealidad afecta ningún supuesto sobre los errores. Por lo tanto, el estimador por MCO siguen siendo BLUE. Pero, en presencia de multicolinealidad:
Las varianzas de los coeficientes estimados \((\widehat{\beta}_{j})\) se incrementan. Lo que reduce los valores \(t\) asociados.
La estimación de los coeficientes del modelo \((\widehat{\boldsymbol \beta})\) son sensibles a las especificaciones. Estos pueden cambiar drásticamente cuando se agregan o eliminan covariables.
Sin embargo, el ajuste general del modelo, y por lo tanto las predicciones, no se verá tan afectado.
3.2.1 Causas de la multicolinealidad
La multicolinealidad se puede deber a múltiples razones, entre las que están:
Con frecuencia se presentan problemas donde intervienen procesos de producción o químicos, donde las covariables son los componentes de un producto y ésos suman una constante.
Variables que son componentes de un sistema pueden mostrar dependencias casi lineales debido a las limitaciones biológicas, físicas o químicas del sistema.
Variables que tienen una tendencia común y evolucionan de forma muy parecida en el tiempo.
Inclusión de variables irrelevantes en el modelo. La información que contienen estas variables ya estarían incluidas en otras y no aportan a la explicación de la variabilidad de la variable respuesta.
Por ejemplo, en los datos del cemento, tenemos que el problema de multicolinealidad se presenta porque: \[ x_{i1} + x_{i2} + x_{i3} + x_{i4} \approx \mbox{constante}. \] En los datos de grasa corporal, el problema es causado por la alta correlación entre el pliegue cutáneo del triceps \((X_{1})\) y la circunferencia del muslo \((X_{2})\).
3.3 Detección de multicolinealidad
Dado que la multicolinealidad provoca una inflación de la varianza, un indicio de este problema está en que aunque el modelo presenta un buen ajuste (un \(R^2\) por ejemplo), las estimaciones de coeficientes asociados a covariables releventas tienen valores \(t\) pequeños. Además, al eliminar covariables, las estimacioes cambian considerablemente.
A manera inicial, la multicolinealidad se puede detectar por medio de la evaluación de la matriz de correlación. Sin embargo, hay indicadores más formales para ello. Estos son los factores de inflación de varianza (VIF), y los índices de condiciones de \(\boldsymbol R\) o \(\boldsymbol Z\).
3.3.1 Factores de inflación de varianza
Dado que \(V(\widehat{\boldsymbol b}) = \sigma^2\boldsymbol R^{-1}\), los elementos de la diagonal de \(\boldsymbol R^{-1}\) son buenos indicadores de multicolinealidad: \[ VIF_j =\{\boldsymbol R^{-1}\}_{jj} = (1-R_{j}^{2})^{-1}, \] donde \(R_{j}^{2}\) es el coeficiente de determinación de ajustar un modelo de \(x_{j}\) en función de las demás covariables. Si \(x_{j}\) es casi ortogonal a las demás covariables, \(R^{2}_{j}\) es pequeño, y por lo tanto, \(\{\boldsymbol R^{-1}\}_{jj}\) cercano a \(1\). Mientras que, si \(x_{j}\) es casi linealmente dependiente a las demás covariables, entonces \(R^{2}_{j}\) es cercano a \(1\) y \(\{\boldsymbol R^{-1}\}_{jj}\) grande.
Por lo tanto, \(VIF_j\) puede ser visto como un factor de cuanto se incrementa \(V(\widehat{b}_{j})\) debido a la colinealidad entre las covariables. De aquí el nombre de factor de inflación de varianza (VIF). Generalmente, uno o mas valores grandes de VIF (\(5\) o \(10\)) es un indicador de problemas de multicolinealidad.
3.3.2 Valores propios de \(\boldsymbol Z'\boldsymbol Z\)
Dado que \(\boldsymbol R= \boldsymbol Z'\boldsymbol Z\) es una matriz simétrica y positiva semi-definida, entonces se puede descomponer de la siguiente forma: \[ \boldsymbol R= \boldsymbol T\boldsymbol \Lambda\boldsymbol T', \] donde \(\boldsymbol T= (\boldsymbol t_{1},\ldots,\boldsymbol t_{k})\) es una matriz ortogonal de vectores propios, y \(\boldsymbol \Lambda\) una matriz diagonal con los valores propios \(\lambda_{j}\), para \(j=1,\ldots,p-1\), en la diagonal principal. Por lo tanto: \[ V(\widehat{\boldsymbol \beta}) = \sigma^{2}\boldsymbol T\boldsymbol \Lambda^{-1}\boldsymbol T'. \] Entonces, \[ V(\widehat{b}_{j}) = \sigma^{2}\sum_{k=1}^{p-1}\frac{t_{jk}^{2}}{\lambda_{k}}. \] De la expresión anterior se puede ver la relación de los valores propios con el VIF: \[ VIF_{j} = \sum_{j=1}^{p-1}\frac{t_{ij}^{2}}{\lambda_{j}}, \] Por lo tanto, uno o más valores propios pequeños pueden inflar la varianza de \(\widehat{b}_{j}\). De aquí salen los indicadores llamados índices de condición y número de condición. Los índices de condición están definidos como: \[ \eta_{j} = \frac{\lambda_{\mbox{max}}}{\lambda_{j}}. \] El número de condición está definido como el máximo índice de condición. Un número de condición mayor de \(100\) es un indicador de multicolinealidad.
3.3.3 Valores singulares de \(\boldsymbol Z\)
El número de condición también se puede calcular a partir de la descomposición en valores singulares (SVD) de la matriz de covariables \(\boldsymbol Z\). Esto es: \[ \boldsymbol Z=\boldsymbol U\boldsymbol D\boldsymbol T', \] donde \(\boldsymbol U\) y \(\boldsymbol T\) son matrices \(n\times (p-1)\) y \((p-1)\times (p-1)\), respectivamente, \(\boldsymbol U\boldsymbol U= \boldsymbol I\) y \(\boldsymbol T'\boldsymbol T= \boldsymbol I\), y \(\boldsymbol D\) es una matriz diagonal con elementos \(\mu_{j}\), \(j=1,\ldots,p-1\), llamados valores singulares. Hay una relación entre los valores singulares de \(\boldsymbol Z\) y los valores propios de \(\boldsymbol Z'\boldsymbol Z\): \[ \boldsymbol Z'\boldsymbol Z= (\boldsymbol U\boldsymbol D\boldsymbol T')'\boldsymbol U\boldsymbol D\boldsymbol T' = \boldsymbol T\boldsymbol D^2\boldsymbol T' = \boldsymbol T\boldsymbol \Lambda\boldsymbol T'. \] El índice de condición de \(\boldsymbol Z\) está definido como: \[ \kappa_{j} = \frac{\mu_{\mbox{max}}}{\mu_{j}}. \] El número de condición de \(\boldsymbol Z\) está definido como el máximo \(\kappa_{j}\). Un número de condición mayor de 10, 15 o 30 es un indicador de problemas de multicolinealidad.
Note que \(\kappa_{j} = \sqrt{\eta_{j}}\). Por lo que el punto de corte de \(10\) para el número de condición de \(\boldsymbol Z\) es equivalente al número de condición de \(100\) para el número de condición de \(\boldsymbol Z'\boldsymbol Z\).
3.3.4 Proporciones de descomposición de varianza
Hay una relación entre el VIF, los valores propios y los valores singulares. Esta es: \[ VIF_{j} = \sum_{j=1}^{p-1}\frac{t_{ij}^{2}}{\lambda_{j}} = \sum_{j=1}^{p-1}\frac{t_{ij}^{2}}{\mu_{j}^2}. \] De aquí salen los indicadores llamados proporciones de descomposición de varianza. Estos se calculan de la siguiente forma: \[ \pi_{ij} = \frac{t_{ij}^2 / \mu_{i}^2 }{VIF_{j}}, j = 1,\ldots, p-1. \] Si se agrupan los \(\pi_{ij}\) en una matriz \((p-1) \times (p-1)\) \(\boldsymbol \pi\), la columna \(j\) son proporciones de la varianza de \(\widehat{\boldsymbol b}\). Valores \(\pi_{ij}\) mayores de \(0.5\) indican problemas de multicolinealidad.
3.4 Datos de cemento
Los VIF para el modelo ajustado para los datos de cemento son los siguientes:
## x1 x2 x3 x4
## 38.49621 254.42317 46.86839 282.51286Aquí vemos que todos los VIFs son muy altos, mostrando que hay problemas graves de multicolinealidad.
Para calcular los índices de condición (a partir de los valores singulares de \(\boldsymbol Z\)) y las proporciones de descomposición de varianza se utiliza la función eigprop() de la librería mctest. Sin embargo, es necesario ajustar :
### escalamiento de variables
cement.scale = as.data.frame(scale(cement)/sqrt(nrow(cement)-1))
### modelo con datos escalados
mod.cement.scale =lm(y~x1+x2+x3+x4,data=cement.scale)
### calculo de los índices de condición y proporciones de descomposición
### de varianza
library(mctest)
eigprop(mod.cement.scale)##
## Call:
## eigprop(mod = mod.cement.scale)
##
## Eigenvalues CI (Intercept) x1 x2 x3 x4
## 1 2.2357 1.0000 0 0.0026 0.0006 0.0015 0.0005
## 2 1.5761 1.1910 0 0.0043 0.0004 0.0050 0.0005
## 3 1.0000 1.4952 1 0.0000 0.0000 0.0000 0.0000
## 4 0.1866 3.4613 0 0.0635 0.0021 0.0465 0.0007
## 5 0.0016 37.1063 0 0.9296 0.9969 0.9471 0.9983
##
## ===============================
## Row 5==> x1, proportion 0.929579 >= 0.50
## Row 5==> x2, proportion 0.996931 >= 0.50
## Row 5==> x3, proportion 0.947067 >= 0.50
## Row 5==> x4, proportion 0.998343 >= 0.50El número de condición \((37.106)\) es muy alto reafirmando el problema de multicolinealidad. Además, también se puede observar que varias de las proporciones de descomposición de varianza son mayores de \(0.5\).
3.5 Datos de grasa corporal
Para el modelo ajustado a los datos de grasa corporal, los VIF son:
## Triceps Thigh Midarm
## 708.8429 564.3434 104.6060Además, los índices de condición y las proporciones de descomposición de varianza son:
### escalamiento de variables
bodyfat.scale = as.data.frame(scale(bodyfat)/sqrt(nrow(bodyfat)-1))
### modelo con datos escalados
mod.bodyfat.scale =lm(Fat~Triceps+Thigh+Midarm,data=bodyfat.scale)
### calculo de los índices de condición y proporciones de descomposición
### de varianza
eigprop(mod.bodyfat.scale)##
## Call:
## eigprop(mod = mod.bodyfat.scale)
##
## Eigenvalues CI (Intercept) Triceps Thigh Midarm
## 1 2.0665 1.0000 0 0.0003 0.0003 0.0006
## 2 1.0000 1.4375 1 0.0000 0.0000 0.0000
## 3 0.9328 1.4884 0 0.0000 0.0004 0.0082
## 4 0.0007 53.3287 0 0.9997 0.9993 0.9912
##
## ===============================
## Row 4==> Triceps, proportion 0.999667 >= 0.50
## Row 4==> Thigh, proportion 0.999292 >= 0.50
## Row 4==> Midarm, proportion 0.991205 >= 0.50Todos estos indicadores muestran que hay problemas de multicolinealidad.
3.6 Solución al problema de multicolinealidad
Los problemas de multicolinealidad se pueden solucionar de las siguientes formas:
recolección de datos adicionales: si se tiene control sobre las covariables, es posible tomar más observaciones para romper con la casi dependencia en \(\boldsymbol X\). Pero esto en muchas casos es díficil por la naturaleza de las covariables. Por ejemplo, sería imposible buscar personas con circunferencia del muslo grande y pliegue cutáneo del tríceps bajo (o viceversa).
re-especificación del modelo: se pueden eliminar del modelo las covariables que me generan el problema de multicolinealidad y que pueden tener poco aporte explicativo dentro del modelo.
Por ejemplo, en los datos de la grasa corporal podemos eliminar la variable asociada al muslo (o al tríceps, pues ambas proporcionan la misma información). Si quitamos esta covariable:
## Triceps Midarm
## 1.265118 1.265118los VIF disminuyen considerablemente. Además, no hay una reducción notable del \(R^2\). Con las tres covariables temenos que \(R^{2}=0.801\). Mientras que al remover Thigh, tenemos que \(R^{2} = 0.786\)
- Uso de estimadores sesgados: Considerando que el estimador por MCO es el mejor estimador lineal insesgado de \(\boldsymbol \beta\), podemos relajar la condición de insesgamiento y buscar estimadores que aunque sean sesgados tengan menor varianza que los estimadores por MCO. Dos de estas alternativas son el estimador de ridge y el estimadores por componentes principales.
3.7 Estimador de ridge
El estimador de ridge tiene como objetivo minimizar la siguiente suma de cuadrados penalizada: \[\begin{equation} \begin{split} S_{k}(\boldsymbol b) &= \sum_{i=1}^{n}(y_{i} - \boldsymbol z_{i}'\boldsymbol b)^{2} + k \sum_{j=1}^{p-1}\boldsymbol b_{j}^2 \\ &= (\boldsymbol y- \boldsymbol Z\boldsymbol b)'(\boldsymbol y- \boldsymbol Z\boldsymbol b) + k ||\boldsymbol b||_{2}^{2}, \end{split} \nonumber \end{equation}\] con \(k \geq 0\) (el cual es seleccionado por el investigador). Lo que lleva a las siguientes ecuaciones normales: \[ (\boldsymbol R+ k \boldsymbol I)\widehat{\boldsymbol b}_{k} = \boldsymbol Z'\boldsymbol y. \] La solución de las ecuaciones normales lleva al estimador ridge: \[ \widehat{\boldsymbol b}_{k} = (\boldsymbol R+ k \boldsymbol I)^{-1}\boldsymbol Z'\boldsymbol y. \] Note que, incluso si \(\boldsymbol R\) es no es invertible, un \(k > 0\) resuelve el problema. Además, la solución depende de \(k\) (por cada \(k\), hay una estimación diferente).
Se puede considerar a \(k\) como un parámetro de contracción. Si \(k \rightarrow 0\), tenemos que \(\widehat{\boldsymbol b}_{R} \rightarrow \widehat{\boldsymbol b}\). Mientras que, si \(k \rightarrow \infty\), encontramos que \(\widehat{\boldsymbol b}_{R} \rightarrow \boldsymbol 0\) (excepto el intercepto).
Ahora veamos las propiedades de \(\widehat{\boldsymbol b}_{k}\). Este se puede expresar como: \[ \widehat{\boldsymbol b}_k = (\boldsymbol R+ k \boldsymbol I)^{-1}\boldsymbol R\boldsymbol y= (\boldsymbol I+ k \boldsymbol R^{-1})^{-1}\widehat{\boldsymbol b}= \boldsymbol C\widehat{\boldsymbol b}. \] Por lo que, su valor esperado es: \[ E(\widehat{\boldsymbol b}_{k}) =\boldsymbol C\boldsymbol b\neq \boldsymbol b, \] de aquí vemos que \(\widehat{\boldsymbol b}_{k}\) es sesgado, y el sesgo aumenta con \(k\) (por lo que este parámetro también es llamado de sesgo). La varianza de \(\widehat{\boldsymbol b}_k\) está dada por: \[ V(\widehat{\boldsymbol b}_{k}) = \sigma^2 \boldsymbol C' \boldsymbol R^{-1} \boldsymbol C. \] A partir de las cantidades anteriores se puede determinar el error cuadrático medio (ECM) de \(\widehat{\boldsymbol b}_{R}\): \[\begin{equation} \begin{split} \mbox{MSE}(\widehat{\boldsymbol b}_{k}) &= \mbox{tr}V(\widehat{\boldsymbol b}_k) + \left[ E(\widehat{\boldsymbol b}_{k}) - \boldsymbol b\right]'\left[ E(\widehat{\boldsymbol b}_{k}) - \boldsymbol b\right] \\ &= \sigma^2\mbox{tr}\left( R^{-1}\boldsymbol C'\boldsymbol C\right) + \boldsymbol b'(\boldsymbol C-\boldsymbol I)'(\boldsymbol C-\boldsymbol I)\boldsymbol b\\ &=\sigma^{2}\sum_{j=1}^{p-1}\frac{\lambda_{j}}{(\lambda_{j}+ k)^2} + \sum_{j=1}^{p-1}\frac{\alpha_j^{2}k^2}{(\lambda_{j}+ k)^2}, \end{split} \nonumber \end{equation}\] donde \(\boldsymbol \alpha= \boldsymbol T'\boldsymbol b\).
Finalmente, la suma de cuadrados de los residuos usando \(\widehat{\boldsymbol b}_{k}\) es: \[ SS_{res}(\widehat{\boldsymbol b}_{k}) =(\boldsymbol y- \boldsymbol Z\widehat{\boldsymbol b})'(\boldsymbol y- \boldsymbol Z\widehat{\boldsymbol b}) + (\widehat{\boldsymbol b}_{k}-\widehat{\boldsymbol b})'\boldsymbol R(\widehat{\boldsymbol b}_{k}-\widehat{\boldsymbol b}) = SS_{res}(\widehat{\boldsymbol b}) + (\widehat{\boldsymbol b}_{k}-\widehat{\boldsymbol b})'\boldsymbol R(\widehat{\boldsymbol b}_{k}-\widehat{\boldsymbol b}). \] A partir de estos resultados, vemos que: (1) Si \(k\) crece, disminuye la varianza, pero aumenta el sesgo. (2) Si \(k\) disminuye, aumenta la varianza, pero disminuye el sesgo. (3) el estimador ridge proporciona un coeficiente de determinación mas pequeño que el estimador por MCO. Sin embargo, las estimaciones de \(\boldsymbol b\) son más estables.
La idea de la regresión de ridge es encontrar un valor de \(k\) tal que \(\mbox{ECM}(\widehat{\boldsymbol b}_{k}) < V(\widehat{\boldsymbol b})\). En la Figura 3.3 podemos ver la representación del ECM del estimador de ridge. A medida que aumenta \(k\), el sesgo incrementa y la varianza disminuye. Además, hay una región de \(k\) donde se puede obtener un ECM del estimador de ridge menor que el que se obtiene por medio de MCO. La idea es encontrar el valor de \(k\) que minimiza el ECM, o por lo menos algún valor en la región donde \(\mbox{ECM}(\widehat{\boldsymbol b}_{k}) < V(\widehat{\boldsymbol b})\).
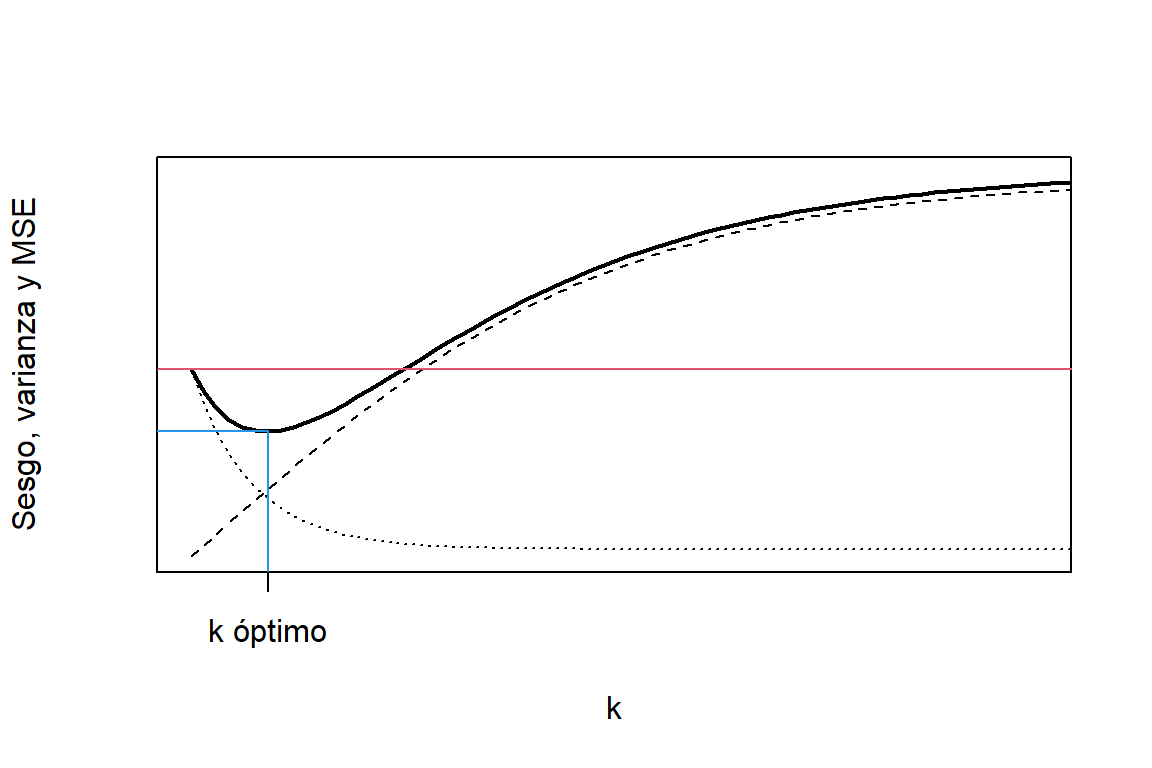
Figure 3.3: Representación del sesgo al cuadrado (linea cortada), varianza (linea punteada) y error cuadrático medio (linea solida) del estimador de ridge. La linea roja representa el error cuadrático medio del estimador por MCO.
Algunos métodos de selección de \(k\) son:
Traza de ridge \(k\): el efecto de \(k\) sobre las estimaciones de \(\widehat{\boldsymbol b}_{k}\) es mas fuerte para valores bajos. De igual forma, si \(k\) es muy grande se introduce mucho sesgo. Por lo que se puede hacer es incrementar \(k\) hasta que parezca que su influencia sobre \(\widehat{\boldsymbol b}_{k}\) se atenúe.
Validación cruzada (CV): sea \(\widehat{y}_{(i),k}\) la estimación de \(E(y_i)\) por medio del estimador de ridge con el parámetro \(k\) y usando una muestra excluyendo la i-ésima observación. La validación cruzada está definida como: \[ CV(k) = \sum_{i=1}^{n} (y_i - \widehat{y}_{(i),k})^2. \] Por lo que la selección de \(k\) es: \[ k_{CV} = \arg \min_{k} CV(k). \]
3.7.1 Datos de cemento
Para ajustar el modelo usando el estimador de ridge podemos usar la función lmridge del paquete lmridge. Primero, ajustamos el modelo usando diferentes valores de \(k\):
library(lmridge)
K = seq(from=0,to=0.3,length.out = 100)
ridge.cement = lmridge(y~., data=cement,K=K,scaling='sc')En el objeto ridge.cement tenemos las estimaciones por el estimador de ridge para \(100\) valores de \(k\) entre \(0\) y \(0.3\). Para observar como cambian las estimaciones para los diferentes valores de \(k\) podemos graficar la traza de ridge así (en términos de las covariables en su escala orginal):
EstRidge.cement = coef(ridge.cement)
plot(K,EstRidge.cement[,2],type='l',ylim=range(EstRidge.cement[,-1]),lwd=2,
ylab='Estimaciones de los coeficientes',xlab='k')
lines(K,EstRidge.cement[,3],col=2,lwd=2)
lines(K,EstRidge.cement[,4],col=3,lwd=2)
lines(K,EstRidge.cement[,5],col=4,lwd=2)
abline(h=0,lty=2)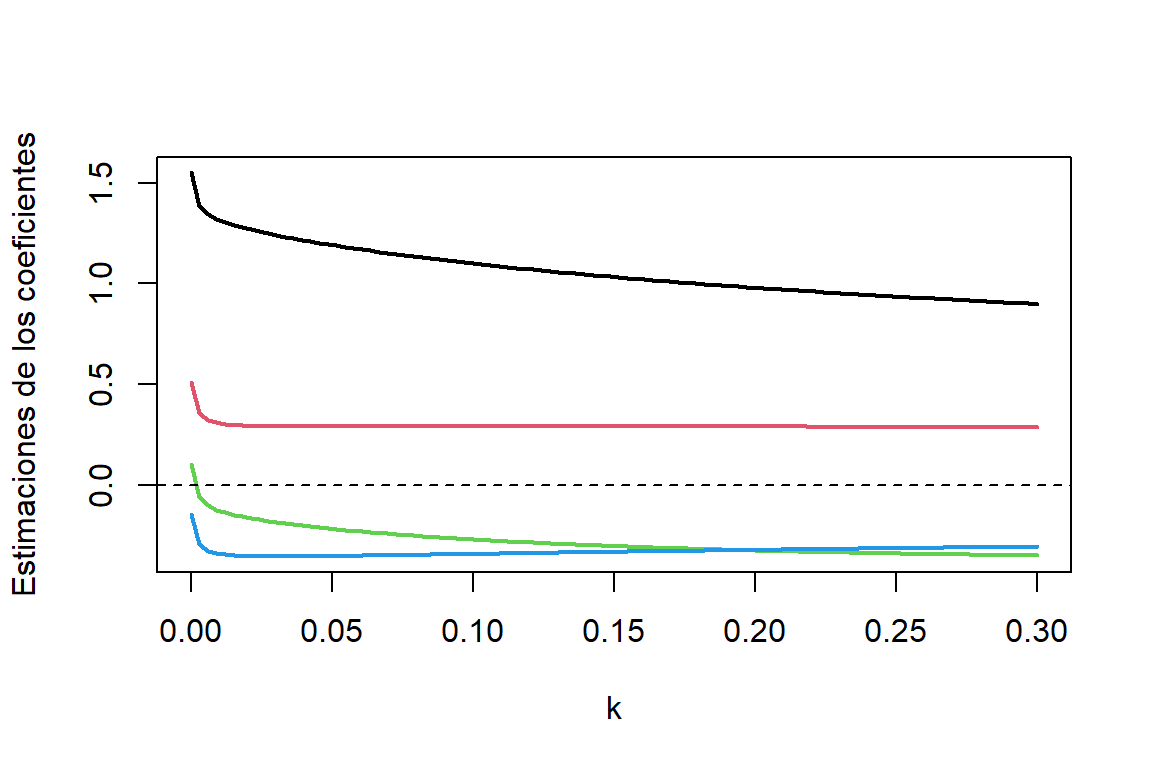
Figure 3.4: Datos de cemento. Traza de ridge. Coeficiente asociado a X1 (negro), coeficiente asociado a X2 (rojo), coeficiente asociado a X3 (verde) y coeficiente asociado a X4 (azul)
En la Figura 3.4 podemos observar que, cuando incrementamos \(k\), las estimaciones cambian rápidamente y luego parecen estabilizarse cuando \(k\) es grande. Además hay un cambio de signo para el coeficiente asociado a X3. También puede usarse plot(mod.r) (traza de ridge para las estimaciones de los coeficientes asociados a las covariables escaladas).
La selección del \(k\) óptimo por medio de validación cruzada (CV) se hace de la siguiente manera:
Criterios.cement = kest(ridge.cement)
plot(K,Criterios.cement$CV,type='l',xlab='K',ylab='validación cruzada')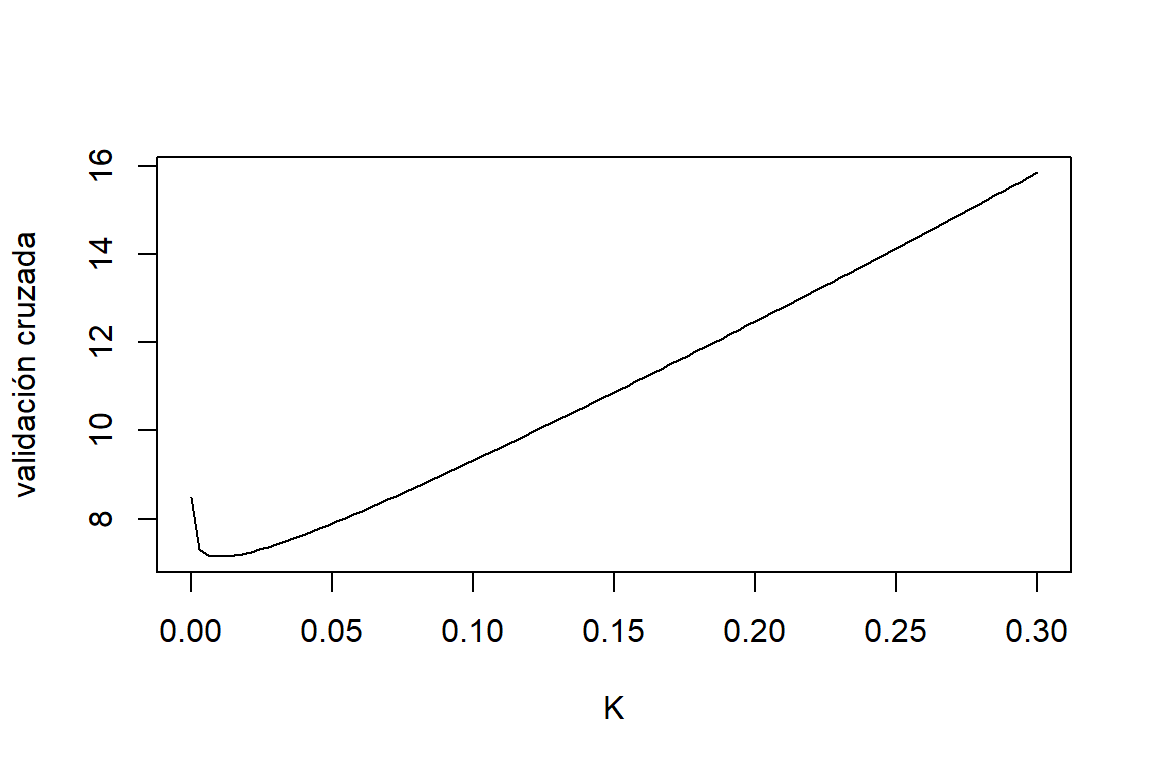
Figure 3.5: Datos de cemento. Validación cruzada.
## [1] 0.009090909Aquí podemos ver que el valor de \(k\) que minimiza la validación cruzada es \(0.009\). El valor óptimo de \(k\) por medio de otros criterios son:
## Ridge k from different Authors
##
## k values
## Minimum CV at K 0.00909
## Minimum GCV at K 0.02424
## Thisted (1976): 0.00581
## LW (lm.ridge) 0.05183
## LW (1976) 0.00797
## HKB (1975) 0.01162
## Dwividi & Srivastava (1978): 0.00291
## Kibria (2003) (AM) 0.28218
## Kibria 2003 (GM): 0.07733
## Kibria 2003 (MED): 0.01718
## Muniz et al. 2009 (KM2): 14.84574
## Muniz et al. 2009 (KM3): 5.32606
## Muniz et al. 2009 (KM4): 3.59606
## Muniz et al. 2009 (KM5): 0.27808
## Muniz et al. 2009 (KM6): 7.80532
## Mansson et al. 2012 (KMN8): 14.98071
## Mansson et al. 2012 (KMN9): 0.49624
## Mansson et al. 2012 (KMN10): 6.63342
## Mansson et al. 2012 (KMN11): 0.15075
## Mansson et al. 2012 (KMN12): 8.06268
## Dorugade et al. 2010: 0.00000
## Dorugade et al. 2014: 101.64433La estimación con \(K=0.0101\) se puede obtener usando la función lmridge:
##
## Call:
## lmridge.default(formula = y ~ ., data = cement, K = 0.0101, scaling = "sc")
##
##
## Coefficients: for Ridge parameter K= 0.0101
## Estimate Estimate (Sc) StdErr (Sc) t-value (Sc) Pr(>|t|)
## Intercept 82.7052 -267.6034 306.3344 -0.8736 0.4052
## x1 1.3146 26.7886 3.9606 6.7637 0.0001 ***
## x2 0.3059 16.4871 5.2766 3.1246 0.0124 *
## x3 -0.1295 -2.8734 3.9360 -0.7300 0.4841
## x4 -0.3432 -19.8985 5.4000 -3.6849 0.0051 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Ridge Summary
## R2 adj-R2 DF ridge F AIC BIC
## 0.97180 0.96240 3.07629 133.92403 23.27712 58.35941
## Ridge minimum MSE= 392.3519 at K= 0.0101
## P-value for F-test ( 3.07629 , 9.74488 ) = 3.013147e-08
## -------------------------------------------------------------------Vemos algunas diferencias con las estimaciones por MCO. Hay un cambio de signo en la estimación del coeficiente asociado a x3. Si embargo, no hay mucha diferencia en las estimaciones de los otros coeficientes. También podemos observar que las covariables x1, x2 y x3 ahora tienen un aporte significativo. Como era de esperarse, hay una disminución del \(R^{2}\), sin embargo es muy leve.
3.8 Estimador por componentes principales
Considere el modelo en su forma canónica: \[ \boldsymbol y^{*} = \boldsymbol Z\boldsymbol T\boldsymbol \alpha+ \boldsymbol \varepsilon, \] donde \(\boldsymbol \alpha= \boldsymbol T'\boldsymbol b\), \((\boldsymbol Z\boldsymbol T)'\boldsymbol Z\boldsymbol T=\boldsymbol \Lambda\), \(\boldsymbol \Lambda\) es una matriz diagonal de valores propios \((\lambda_1,\ldots,\lambda_p)\) de \(\boldsymbol Z'\boldsymbol Z\), y \(\boldsymbol T= (\boldsymbol t_{1},\ldots,\boldsymbol t_{p-1})\) es la matriz ortogonal de vectores propios asociados \(\boldsymbol \Lambda\).
Las columnas de \(\boldsymbol P= \boldsymbol Z\boldsymbol T= (\boldsymbol p_{1},\ldots,\boldsymbol p_{p-1})\) son un conjunto de regresores ortogonales (llamados componentes principales): \[ \boldsymbol p_{k} = \sum_{j=1}^{p-1} t_{kj}\boldsymbol z_{j}. \]
El estimador de \(\boldsymbol \alpha\) por MCO es: \[ \widehat{\boldsymbol \alpha}= (\boldsymbol P'\boldsymbol P)^{-1}\boldsymbol P'\boldsymbol y^{*} = \boldsymbol \Lambda^{-1}\boldsymbol P'\boldsymbol y^{*}, \] y la varianza de \(\widehat{\boldsymbol \alpha}\) es: \[ V(\widehat{\boldsymbol \alpha}) = \sigma^{2}(\boldsymbol P'\boldsymbol P)^{-1} = \sigma^{2}\boldsymbol \Lambda^{-1}. \] De aquí podemos ver que valores propios de \(\boldsymbol R\) están asociados con la varianza de los coeficientes de regresión. Si \(\lambda_j=1\) (para \(j=1,\ldots,p\)), las covariables originales son ortogonales. Mientras que valores propios cercanos a cero indican problemas de multicolinealidad dado que inflan la varianza de \(\widehat{\boldsymbol \alpha}\).
Note que, para \(\widehat{\boldsymbol b}= \boldsymbol T\widehat{\boldsymbol \alpha}\), tenemos: \[ V(\widehat{\boldsymbol b}) = V(\boldsymbol T\widehat{\boldsymbol \alpha}) =\sigma^{2}\boldsymbol T\boldsymbol \Lambda^{-1}\boldsymbol T' = \sigma^{2} \sum_{j=1}^{p-1}\frac{\boldsymbol t_{j}\boldsymbol t_{j}'}{\lambda_{j}}, \] lo que implica que \(V(\widehat{b}_{k}) = \sigma^{2} \sum_{j=1}^{p-1}t_{kj}^{2}/\lambda_{j}\), la varianza de \(\widehat{b}_j\) es una combinación lineal de los valores propios.
Para combatir el problema de multicolinealidad, la idea de la regresión por componentes principales es usar un subconjunto de \(\boldsymbol P\) como regresores (en vez de todos los compontes). Para esto, eliminamos los componentes principales \((\boldsymbol p_{r+1},\ldots,\boldsymbol p_{p-1})\) asociados a los valores propios cercanos a cero \((\lambda_{r+1},\ldots,\lambda_{p-1})\). Aquí estamos asumiendo que \(\lambda_1 \leq \lambda_2 \leq \ldots \leq \lambda_{p-1}\). Esto es, \[ \widehat{\boldsymbol \alpha}_{r} = (\overbrace{\widehat{\alpha}_{1},\widehat{\alpha}_{2},\ldots, \widehat{\alpha}_{r}}^{r},\overbrace{0, \ldots,0}^{p-1-r})'. \] De esta forma el estimador de \(\boldsymbol b\) por CP está dado por: \[ \widehat{\boldsymbol b}_{r} = \boldsymbol T\widehat{\boldsymbol \alpha}_{r} =\sum_{l=1}^{r} \boldsymbol t_l \widehat{\alpha}_l, \]
El sesgo de \(\widehat{\boldsymbol b}_{r}\) es igual a: \[ \widehat{\boldsymbol b}_{r} - \boldsymbol b= \sum_{l=1}^{r} \boldsymbol t_l \widehat{\alpha}_l - \sum_{l=1}^{p-1} \boldsymbol t_l \alpha_l = - \sum_{l = r+1}^{p-1} \boldsymbol t_l \alpha_l. \] La varianza de \(\widehat{\boldsymbol b}_{r}\) es: \[ V(\widehat{\boldsymbol b}_{r}) = \boldsymbol TV(\widehat{\boldsymbol \alpha}_{r})\boldsymbol T' = \sigma^{2}\sum_{l=1}^{r} \lambda_{l}^{-1}\boldsymbol t_{l}\boldsymbol t_{l}' \leq \sigma^{2} \sum_{l=1}^{p-1}\lambda_l^{-1}\boldsymbol t_{l}\boldsymbol t_{l}' = V(\widehat{\boldsymbol b}). \] Por lo tanto, al eliminar componentes principales se aumenta el sesgo, pero se disminuye la varianza de \(\widehat{\boldsymbol b}_r\). Finalmente, el ECM de \(\widehat{\boldsymbol b}_r\) está dado por: \[ MSE(\widehat{\boldsymbol b}_r) = \sigma^{2}\sum_{i=1}^{r}\frac{1}{\lambda_l} + \sum_{l=r+1}^{p-1}\alpha_l^2. \]
3.8.1 Datos de cemento
Antes de ajustar el modelo vamos a escalar las variables
escalar <- function(x) {(x-mean(x)) / sqrt(sum((x-mean(x))^2))}
X = as.matrix(cement[,1:4])
y.e = escalar(cement$y)
Z = apply(cement[,1:4],2,escalar)A partir de las variables escaladas podemos calcular los vectores y valores propios:
## [1] 2.235704035 1.576066070 0.186606149 0.001623746Aquí podemos observar que un valor propio es cercano a cero, por lo que lo podemos eliminarlo para remediar el problema de multicolinealidad:
##
## Call:
## lm(formula = y.e ~ P[, -4] - 1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.058393 -0.036851 0.006961 0.022836 0.073963
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## P[, -4]1 -0.656958 0.028271 -23.238 4.93e-10 ***
## P[, -4]2 -0.008309 0.033671 -0.247 0.8101
## P[, -4]3 0.302770 0.097856 3.094 0.0114 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.04227 on 10 degrees of freedom
## Multiple R-squared: 0.9821, Adjusted R-squared: 0.9768
## F-statistic: 183.2 on 3 and 10 DF, p-value: 4.895e-09Las estimaciones de los coeficientes \((\boldsymbol b)\) para las variables escaladas:
## [,1]
## [1,] 0.51297502
## [2,] 0.27868114
## [3,] -0.06078483
## [4,] -0.42288461La matriz de varianza de \(\boldsymbol b_{r}\) es:
sigma2.pc = sum(PCR.cement$residuals^2)/(13-4)
Var.b = sigma2.pc*T.mat%*%diag(c(1/lambda[1:3],0))%*%t(T.mat)
Var.b## [,1] [,2] [,3] [,4]
## [1,] 0.005382414 -0.0022868445 0.004028698 -0.0013467849
## [2,] -0.002286844 0.0015500408 -0.002015159 0.0001440783
## [3,] 0.004028698 -0.0020151593 0.004925579 -0.0014780352
## [4,] -0.001346785 0.0001440783 -0.001478035 0.0009294415