Capítulo 8 Modelo para conteos
8.1 Casos de estudio
8.1.1 Ataques de epilepsia
Vamos a considerar de nuevo los datos del ensayo clínico sobre epilepsia (data(epilepsy) de la librería HSAUR2).
8.1.2 Muertes por enfermedades cardiovasculares en doctores del Reino Unido
Los datos bs1 de la librería ACSW muestran el número de doctores muertos por enfermedades coronarias entre médicos varones \(10\) años después de seguimiento por grupos de edad y condición de tabaquismo. De igual forma, la base de datos contiene el número de total de años-personas de observación en el momento de análisis. En la Figura 8.1 podemos observar la tasa de mortalidad, por 100,000 personas, crece por grupo de edad, y es generalmente, mayor para los fumadores.
library(ACSWR)
data(bs1)
plot(bs1$Age_Cat, 100000*(bs1$Deaths/bs1$Person_Years),col=bs1$Smoke_Ind+1,
xlab='grupo de edad',ylab='muertes por 100,000 personas-año',pch=20,xaxt='n')
axis(1,1:5,bs1$Age_Group[1:5])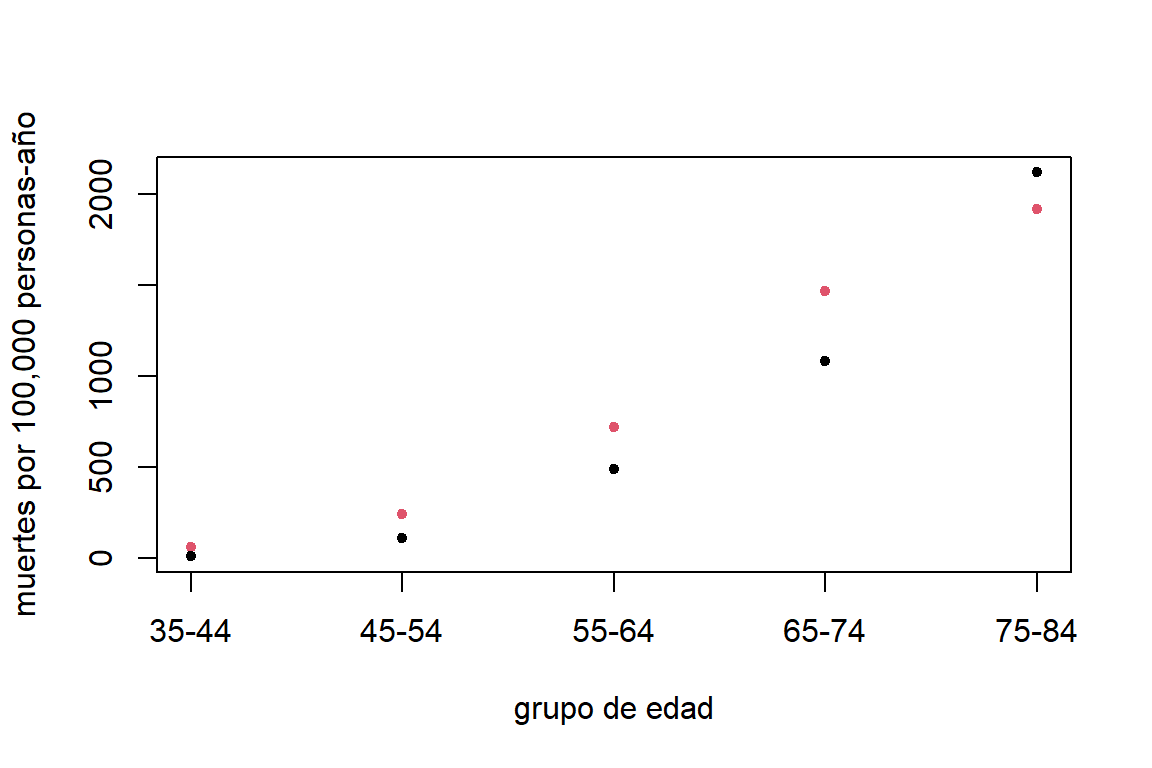
Figure 8.1: Datos de muertes cardiovasculares. Tasa de muertes por enfermedades cardiovasculares en doctores del Reino Unido por grupo de edad. Los puntos rojos corresponden a fumadores y los negros a no fumadores.
A partir de estos datos surgen las siguientes preguntas: ¿La tasa de mortalidad es mayor para los fumadores que para los no fumadores? y ¿El efecto diferencial está relacionado con la edad?
8.1.3 Número de cangrejos satélites
Los datos crabs de la librería asbio son de un estudio sobre \(173\) hembras de cangrejos herradura en una isla en el Golfo de México. Durante el periodo de desove, el macho se adhiere a las hembras cuando estas van a la playa a excavar un agujero en la arena para poner racimos de huevos. Esto con el fin de que puedan fecundar los huevos (fecundación externa). Dada la competencia, las hembras suelen llegar a la playa con varios machos adheridos a ella. A este grupo de cangrejos se les llama satélites. Aquí, nuestra variable de respuesta es el número de satélites que tiene cada hembra. Mientras que las posibles covariables son:
color: color (1, medio-claro; 2, medio; 3, medio-oscuro; 4,oscuro).spine: condición de la espina dorsal (1, ambos bien; 2, uno gastado o roto; 3, ambos gastados o rotos).width: ancho del caparazón (cm).weight: peso (kg)
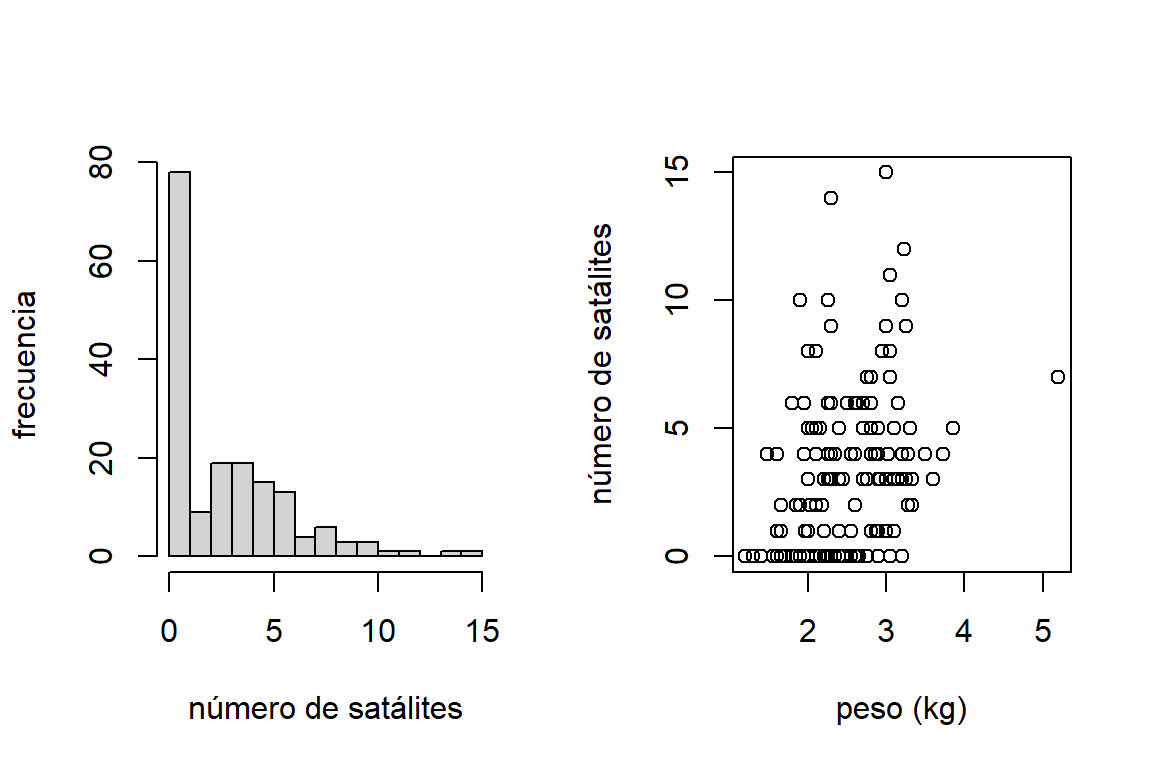
Figure 8.2: Datos de cangrejos satélites. Histograma del número de satélites por hembra (izquierda) y diagrama de dispersión del número de satélites en función del peso de la hembra (derecha)
8.2 Modelo Poisson
La distribución Poisson es comúnmente usada para modelar el número de eventos aleatorios que ocurren en un intervalo de tiempo o espacio determinado. Esta distribución también se aplica como una aproximación de la binomial cuando \(n\) es grande y \(\pi\) es pequeño. En este caso, la binomial\((n_i, \pi_i)\) converge hacia una Poisson\((\mu=n\pi)\).
El modelo Poisson se expresa como: \[ y_i\sim \mbox{Poisson}(\lambda_i), \quad i=1,...,n, \text{ donde } \log \lambda_i=\boldsymbol x'_i\boldsymbol \beta, \] donde \(\boldsymbol x_i\) es el vector de covariables asociada al individuo \(i\). Este modelo asume que: \[ E(y_i|\boldsymbol x_i)=V(y_i|\boldsymbol x_i)=\lambda_i. \] Es decir, la media es igual a la varianza.
8.2.1 Modelo de conteo con offset
En algunos casos los conteos \(y_i\) son proporcionales a un índice \(t_i\) (intervalo de tiempo, área de espacio, tamaño de población). Cuando \(t_i\) no es fijo, se debe incluir un término llamado offset. En este caso, es preferible modelar la tasa \(y_i/t_i\) con valor esperado igual a \(\lambda_i/t_i\).
Por lo tanto, el predictor lineal queda de la forma:
\[ \log\left(\frac{\lambda_i}{t_i}\right)=\boldsymbol x'_i\boldsymbol \beta, \] donde el término \(\log t_i\) es llamado offset. Por lo que \(\log\lambda_i=\boldsymbol x_i'\boldsymbol \beta+\log t_i\). Entonces, el valor esperado de \(y_i\) es:
\[ \lambda_i=t_i \exp(\boldsymbol x_i'\boldsymbol \beta). \] #### Muertes por enfermedades cardiovasculares en doctores del Reino Unido
Dado que los tamaños de la población por grupo de edad son diferentes (hay menos personas en los grupos de edad mayores), debemos considerar esto en el modelo por medio del offset. En este caso el modelo propuesto para el número de doctores muertos por enfermedades cardiovasculares en la \(i\)-ésima categoría \((y_i)\) puede ser: \[ y_i \sim \mbox{Poisson}(\lambda_i), \] donde: \[ \log \lambda_i = \beta_0 + \mbox{smoke}_i\beta_1 + \mbox{ageCat1}_i\beta_2 + \mbox{ageCat2}_i\beta_3 + \mbox{ageCat3}_i\beta_4 + \mbox{ageCat4}_i\beta_5 + \log(t_i), \] smoke\(_i=1\) si la \(i\)-ésima categoría corresponde a fumadores; smoke\(_i=0\) si lo contrario; \(t_i\) es el número de doctores en riesgo asociados al grupo \(i\), ageCat\(j\) corresponde a las variables indicadores asociadas al grupo de edad, con \([35,44]\) como referencia.
El ajuste del modelo es
poisson.doctor = glm(Deaths ~ Smoke_Ind + Age_Group + offset(log(Person_Years)),
family = poisson(link = "log"), data = bs1)
summary(poisson.doctor)##
## Call:
## glm(formula = Deaths ~ Smoke_Ind + Age_Group + offset(log(Person_Years)),
## family = poisson(link = "log"), data = bs1)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -7.9193 0.1918 -41.298 < 2e-16 ***
## Smoke_Ind 0.3545 0.1074 3.302 0.00096 ***
## Age_Group45-54 1.4840 0.1951 7.606 2.82e-14 ***
## Age_Group55-64 2.6275 0.1837 14.301 < 2e-16 ***
## Age_Group65-74 3.3505 0.1848 18.131 < 2e-16 ***
## Age_Group75-84 3.7001 0.1922 19.249 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 935.067 on 9 degrees of freedom
## Residual deviance: 12.132 on 4 degrees of freedom
## AIC: 79.2
##
## Number of Fisher Scoring iterations: 4Estos datos sugieren que, luego de tener en cuenta el efecto de la edad, los fumadores tienen una tasa de mortalidad \(\exp(\widehat{\beta}_1)=1.42\) mayor que los no fumadores.
Para simplificar el modelo, y evaluar efectos de interacción, uno podría tomar la categoría de edad de forma numérica de la siguiente forma: *age\(=1,2,\ldots,5\) para las categorías \(35-44,45-54,\ldots,75-84\). Así podemos proponer un modelo de la forma: \[ \log \lambda_i = \beta_0 + \mbox{smoke}_i\beta_1 + \mbox{age}_i\beta_2 + \mbox{age}^2_i\beta_3 + \mbox{smoke}_i\mbox{age}_i\beta_4 + \log(t_i), \] El efecto de la interacción se incluye para evaluar si la diferencia en la tasa de muertes entre fumadores y no fumadores cambia con el aumento de la edad. El ajuste del modelo es:
bs1$Age = c(1:5,1:5)
poisson.doctor2 = glm(Deaths ~ Smoke_Ind+Age+I(Age^2)+Smoke_Ind*Age + offset(log(Person_Years)),
family = poisson(link = "log"), data = bs1)
summary(poisson.doctor2)##
## Call:
## glm(formula = Deaths ~ Smoke_Ind + Age + I(Age^2) + Smoke_Ind *
## Age + offset(log(Person_Years)), family = poisson(link = "log"),
## data = bs1)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -10.79176 0.45008 -23.978 < 2e-16 ***
## Smoke_Ind 1.44097 0.37220 3.872 0.000108 ***
## Age 2.37648 0.20795 11.428 < 2e-16 ***
## I(Age^2) -0.19768 0.02737 -7.223 5.08e-13 ***
## Smoke_Ind:Age -0.30755 0.09704 -3.169 0.001528 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 935.0673 on 9 degrees of freedom
## Residual deviance: 1.6354 on 5 degrees of freedom
## AIC: 66.703
##
## Number of Fisher Scoring iterations: 4Estos resultados también muestran que, en promedio, los fumadores tienen una tasa de mortalidad \(4\) veces más alta que los no fumadores. Sin embargo, esta diferencia se atenúa a medida que la edad aumenta (efecto interacción negativo). Esto lo podemos ver forma gráfica en la Figura 8.3.
plot(bs1$Age, 100000*(bs1$Deaths/bs1$Person_Years),col=bs1$Smoke_Ind+1,
xlab='grupo de edad',ylab='muertes por 100,000 personas-año',pch=20,xaxt='n')
axis(1,1:5,bs1$Age_Group[1:5])
pred.tasa = 100000*poisson.doctor2$fitted.values/bs1$Person_Years
lines(1:5,pred.tasa[bs1$Smoke_Ind==0],lwd=2)
lines(1:5,pred.tasa[bs1$Smoke_Ind==1],col=2,lwd=2)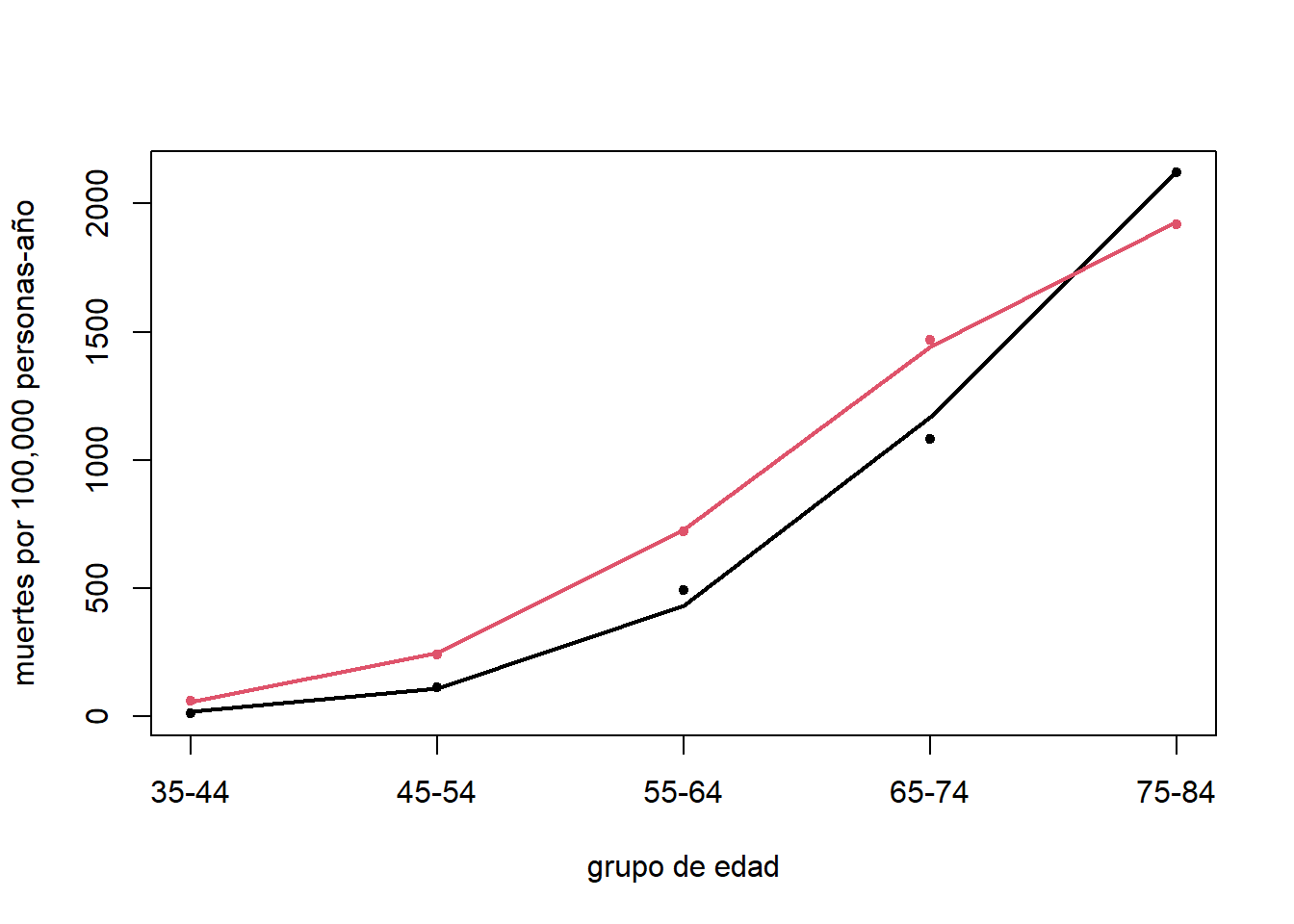
Figure 8.3: Datos de muertes cardiovasculares. Estimación de la tasa de muertes de doctores del Reino Unido por grupo de edad para fumadores(línea roja) y no fumadores (línea negra).
8.3 Sobredispersión
El modelo Poisson asume que \(V(y) = E(y)\). Sin embargo, es común encontrar datos en que la varianza crece más rápido que la media, provocando sobredispersión. En este caso, el estimador por máxima verosimilitud del modelo Poisson sigue proporcionando estimaciones consistentes para la media (estimaciones insesgadas). Sin embargo, los errores estándar estarán mal calculados (generalmente más pequeños).
Para modelar datos de tipo conteo en presencia de sobredispersión se puede asumir una distribución binomial negativa. Esta incluye un parámetro adicional que cuantifica la sobredispersión.
8.3.1 Distribución binomial negativa
La distribución binomial negativa parte de una mezcla de una distribución Poisson con una gamma. Esto es: \[ y | \lambda \sim \mbox{Poisson}(\lambda), \mbox{ donde } \lambda\sim \mbox{gamma}(k,\mu). \] La función de densidad de \(\lambda\) es:
\[ f(\lambda;k,\mu)=\frac{(k/\mu)^k}{\Gamma(k)}\exp\left(-\frac{k\lambda}{\mu}\right)\lambda^{k-1}. \]
Entonces tenemos: \[ E(\lambda)=\mu \mbox{ y } V(\lambda)=\mu^2/k. \] La distribución binomial negativa (también llamada Poisson-gamma) se obtiene al marginalizar \(y\). Esto es: \[ f(y;\mu,k)=\int f(y|\lambda)f(\lambda)d\lambda. \]
La función de densidad de la binomial negativa queda definida como:
\[ f(y;\mu,k)=\frac{\Gamma(y+k)}{\Gamma(k)\Gamma(y+1)}\left( \frac{\mu}{\mu+k}\right)^y \left( \frac{k}{\mu+k} \right)^k \] para \(y=0,1,...\) Si definimos \(\gamma=1/k\), tenemos que:
\[ E(y)=\mu \mbox{ y } V(y)=\mu(1+\gamma\mu), \] para \(\gamma>0\) (llamado parámetro de sobredispersión). La distribución de probabilidad de la distribución binomial negativa se puede observar en la Figura 8.4. Aquí vemos que a medida que aumenta \(\gamma\), la probabilidad de valores extremos es más alta.
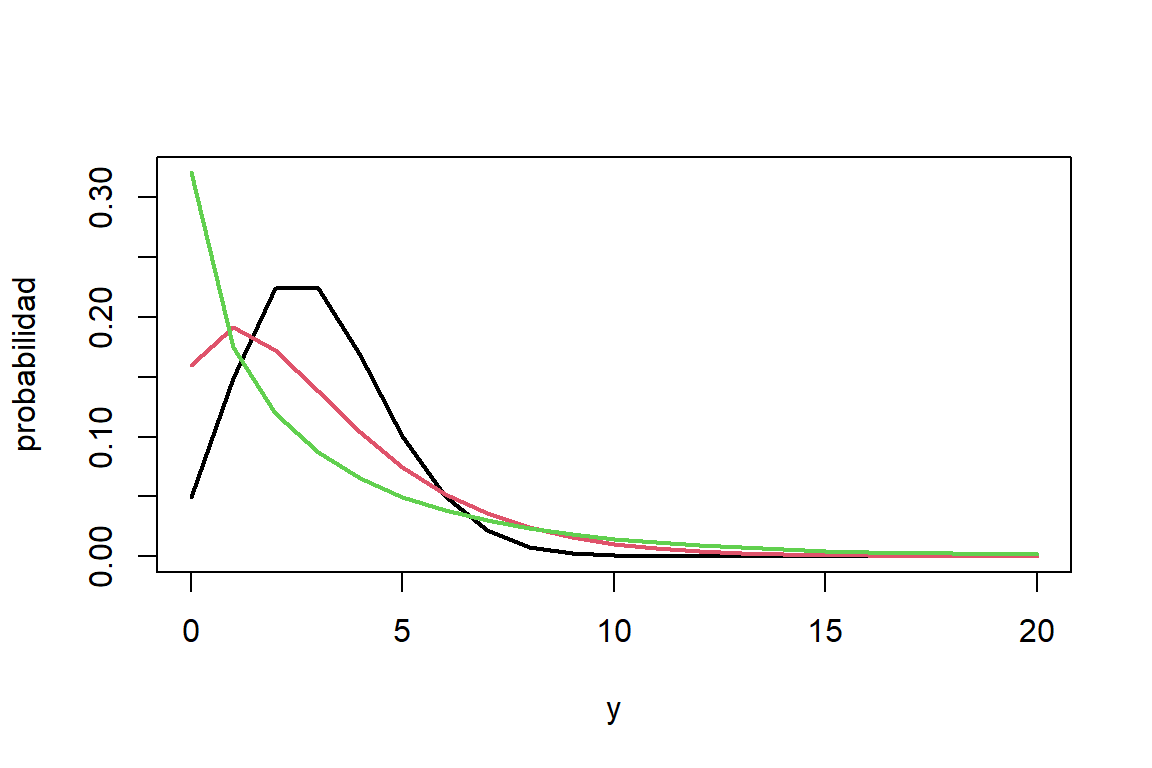
Figure 8.4: Función de probabilidad de Poisson(3) (negro), binomial negativa (3,0.5) (rojo), binomial negativa (3,1.5) (verde).
Dado que \(\gamma>0\), el modelo binomial negativo no puede modelar datos con subdispersión.
8.3.2 Modelo binomial negativo
El modelo binomial negativo se expresa de la siguiente forma: \[ y_i|\lambda_i\sim \mbox{binomial negativa}(\mu_i,\gamma), \]
donde
\[ \mu_i=\exp(\boldsymbol x'_i\boldsymbol \beta). \] Por lo cuál: \[ E(y_i)=\mu_i\mbox{ y } V(y_i)=\mu_i(1+\gamma\mu_i). \] La estimación de los parámetros \((\boldsymbol \beta,\gamma)\) se hace por máxima verosimilitud.
8.3.2.1 Ataques epilépticos
Para los datos de los ataques epilépticos se propone el siguiente modelo: \[ y_i \sim \mbox{Poisson}(\lambda_i), \mbox{ donde } \log \lambda_i = \beta_0 + \mbox{treatment}_i\beta_1 + \mbox{base}_i\beta_2, \] donde \(y_i\) es el número de ataques epiléptivos en dos semanas luego de cuatro semanas de tratamiento; treatment\(_i=1\) si el \(i\)-ésimo paciente recibió el tratamiento progabida y treatment\(_i=0\) si lo contrario. Los resultados del ajuste son:
epilepsy4= HSAUR2::epilepsy[HSAUR2::epilepsy$period==4,]
modPois = glm(seizure.rate~treatment+base,data=epilepsy4,family=poisson)
summary(modPois)##
## Call:
## glm(formula = seizure.rate ~ treatment + base, family = poisson,
## data = epilepsy4)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.214772 0.085543 14.201 < 2e-16 ***
## treatmentProgabide -0.315159 0.098469 -3.201 0.00137 **
## base 0.021536 0.001039 20.733 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 476.25 on 58 degrees of freedom
## Residual deviance: 149.68 on 56 degrees of freedom
## AIC: 343.44
##
## Number of Fisher Scoring iterations: 5Los resultados del ajuste del modelo Poisson muestran que el tratamiento es altamente significativo. Por lo que, se puede concluir que la progabida reduce el número de ataques epilépticos. Sin embargo, estos datos presenta sobredispersión. Esto se puede verificar por medio de la razón del estadístico \(\chi^2\) de Pearson y los grados de libertad:
## [1] 2.525656Por esta razón se puede estimar el modelo binomial negativo:
\[
y_i \sim \mbox{binomial negativa}(\mu_i,\gamma), \mbox{ donde } \log \mu_i = \beta_0 + \mbox{treat}_i\beta_1 + \mbox{base}_i\beta_2.
\]
El ajuste en R se puede hacer utilizando la función glm.nb de la librería MASS:
##
## Call:
## glm.nb(formula = seizure.rate ~ treatment + base, data = epilepsy4,
## init.theta = 4.483069947, link = log)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.080878 0.153419 7.045 1.85e-12 ***
## treatmentProgabide -0.327892 0.168163 -1.950 0.0512 .
## base 0.025017 0.002688 9.308 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for Negative Binomial(4.4831) family taken to be 1)
##
## Null deviance: 174.166 on 58 degrees of freedom
## Residual deviance: 70.124 on 56 degrees of freedom
## AIC: 313.32
##
## Number of Fisher Scoring iterations: 1
##
##
## Theta: 4.48
## Std. Err.: 1.55
##
## 2 x log-likelihood: -305.324Las estimaciones del modelo binomial negativo son similares a las del ajuste del modelo Poisson. Sin embargo, vemos que los errores estándar son más grandes. Además, el valor-\(p\) del efecto asociado al tratamiento es mayor. Si consideramos \(\alpha=0.05\), el efecto del tratamiento no es significativo.
Podemos evaluar si se presentan problemas de sobredispersión con el ajuste del modelo binomial negativo:
## [1] 1.036141Este resultado sugiere que la varianza está bien estimada. Comparando criterios de información, el modelo binomial negativo presenta un mejor ajuste que el modelo Poisson:
## [1] 321.6337## [1] 349.67738.4 Inflación de ceros
En ocaciones, los datos muestran mayor frecuencia de ceros de los que la distribución Poisson y binomial negativa permiten. Por ejemplo, en datos de cangrejos herradura, hay muchas hembras que llegan a la playa sin ningún satélite. La Figura 8.2 muestra que una distribución bimodal para el número de satélites.
Distribución con inflación de ceros Este tipo de datos se pueden modelar con una mezcla de distribuciones donde \(Y=0\) cuando \(Z=1\), y \(Y\) sigue una distribución particular cuando \(Z=0\) (la cual permite la posibilidad de ceros). Por ejemplo, la distribución Poisson con inflación de ceros (ZIP) se puede representar como: \[ y\sim\begin{cases} 0 \qquad & \text{con probabilidad}\quad \phi, \\ \mbox{Poisson}(\lambda) \quad & \text{con probabilidad}\quad 1-\phi. \end{cases} \] La probabilidad de que \(y\) sea igual a cero es: \[ P(y=0) = \phi + (1-\phi) \exp \left(-\lambda\right). \] Mientras que para \(y>0\) se tiene: \[ P(y=j) =(1-\phi) \exp \frac{\left(-\lambda\right)\lambda^j}{j!}, j=1,2,\ldots. \] El valor esperado y la varianza de \(y\) son: \[ E(y) = E(E(y|z)) = (1-\phi)\lambda, \mbox{ y } V(y)= (1-\phi)\lambda \left( 1+ \phi\lambda\right). \] Note que la distribución ZIP permite sobredispersión.
De igual forma, se puede tener un modelo binomial negativo con inflación de ceros (ZINB): \[ y\sim \begin{cases} 0 \qquad & \text{con probabilidad } \phi, \\ \mbox{binomial negativa}(\mu,\gamma) \quad & \text{con probabilidad } 1-\phi. \end{cases} \] En este modelo, la probabilidad de que \(y\) sea igual a cero es: \[ P(y=0) = \phi + (1-\phi) \left( 1 + \gamma \mu \right)^{-1/\gamma}. \] Mientras que el valor esperado y varianza son: \[ E(y)= (1-\phi)\mu \mbox{ y } V(y) = (1-\phi) \mu \left[1+\mu(\gamma+\phi)\right]. \]
Otra alternativa para modelar exceso de ceros es a través del mdelo Hurdle. Este asume que hay un proceso Bernoulli que determina si el conteo es igual a cero o es positivo. Si ocurre lo segundo, una distribución truncada determina la probabilidad del conteo. La distribución se puede expresar como: \[\begin{equation} P(y = j)=\begin{cases} \pi & j=0, \\ (1-\pi)\frac{f(y|\theta)}{1-f(0|\theta)} & j >0. \end{cases} \tag{8.1} \end{equation}\]
A diferencia del modelo ZI, aquí la probabilidad de \(y=0\) solo está determinado por \(\pi\) (no por una mezcla de distribuciones).
Por ejemplo, el modelo Hurdle Poisson (HP) se define como: \[ P(y = j)=\begin{cases} \pi \qquad & j=0, \\ (1-\pi)\frac{\lambda^{j}\exp(-\lambda)}{j! [1-\exp(-\lambda)]} & j >0. \end{cases} \] El valor esperado y varianza de \(y\) son: \[\begin{equation} E(y)= (1-\pi) E(y | y > 0) \mbox{ y } V(y) = (1-\pi) V(y | y > 0) + \pi(1-\pi)E(y | y>0)^2, \tag{8.2} \end{equation}\] donde: \[ E(y | y > 0) = \frac{\lambda}{1- \exp(-\lambda)} \mbox{ y } V(y|y>0) = \frac{\mu}{1-\exp(-\lambda)} + \exp(-\lambda)E(y | y >0)^2. \] También, se tiene la distribución Hurdle binomial negativa (HNB), definiendo \(f(y)\) como la distribución binomial negativa en (8.1).
8.4.1 Modelo de inflación de ceros
El modelo Poisson con ceros inflados (ZIP) se expresa de la siguiente forma: \[ y_i \sim \begin{cases} 0 \qquad & \text{con probabilidad } \phi_i, \\ \mbox{Poisson}(\lambda_i) \quad & \text{con probabilidad } 1-\phi_i. \end{cases} \]
Los parámetros \(\phi_i\) y \(\lambda_i\) pueden ser modelados a través de covariables:
\[ \mbox{logit } \phi_i=\boldsymbol x'_{1i}\boldsymbol \beta_1 \quad\text{y}\quad \log\lambda_i=\boldsymbol x'_{2i}\boldsymbol \beta_2. \]
En presencia de una sobredispersión mayor, el modelo de ceros inflados puede combinarse con una distribución binomial negativa. Esto es: \[ y_i\sim \begin{cases} 0 & \text{con probabilidad } \phi_i, \\ \text{binomial negativa}(\mu_i,\gamma)& \text{con probabilidad } 1-\phi_i. \end{cases} \] De igual forma \(\mu_i\) y \(\phi_i\) se pueden modelar por medio de covariables.
8.4.2 Modelo Hurdle
El modelo Hurdle lo podemos expresar de la forma: \[ P(Y_i=j)=\begin{cases} \pi_i & j=0,\\ (1-\pi_i)\frac{f(j;\theta_i)}{1-f(0;\theta_i)} & j=1,2,\ldots, \end{cases} \] donde la función \(f(\cdot;\theta_i)\) puede ser una Poisson o binomial negativa. Al igual que el modelo ZI, \(\pi_i\) se puede modelar usando un modelo logístico y un modelo log-lineal para \(\lambda_i\) (Poisson) o \(\mu_i\) (binomial negativo).
8.4.3 Número de cangrejos satélites
Para los datos de los cangrejos satélites podemos estimar un modelo con inflación de ceros con:
\[
\mbox{logit } \phi_i=\beta_{10} + \mbox{weight}_i\beta_{11} \quad\text{y}\quad \log\lambda_i=\beta_{20} + \mbox{weight}_i\beta_{21}.
\]
En R, se puede utilizar la funcion zeroinfl de la librería pscl
library(pscl)
# modelo ZIP
ZIP.sat = zeroinfl(satell~weight | weight,data=crabs,dist='poisson')
# modelo ZINB
ZINB.sat = zeroinfl(satell~weight | weight,data=crabs,dist='negbin')Mientras que los modelos Hurdle se pueden estimar con la función hurdle:
# modelo HP
HP.sat = hurdle(satell~weight | weight,data=crabs,dist='poisson')
# modelo HNB
HNB.sat = hurdle(satell~weight | weight,data=crabs,dist='negbin')Los ajustes los podemos comparar con criterios de información:
## [1] 747.8175## [1] 731.2937## [1] 747.7903## [1] 731.0369Aquí vemos que los modelos ZINB y HNB proporcionan mejores ajustes. Las estimaciones del modelo ZINB son:
##
## Call:
## zeroinfl(formula = satell ~ weight | weight, data = crabs, dist = "negbin")
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## -1.3647 -0.7899 -0.3112 0.5086 3.8908
##
## Count model coefficients (negbin with log link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.8979 0.3053 2.941 0.00327 **
## weight 0.2171 0.1119 1.941 0.05229 .
## Log(theta) 1.6013 0.3553 4.507 6.57e-06 ***
##
## Zero-inflation model coefficients (binomial with logit link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 3.7565 0.9841 3.817 0.000135 ***
## weight -1.9131 0.4322 -4.426 9.59e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Theta = 4.9595
## Number of iterations in BFGS optimization: 19
## Log-likelihood: -352.8 on 5 DfLos resultados muestran que la probabilidad de que no hayan satélites disminuye cuando la hembra tiene mayor peso. De igual forma, la media incrementa con el peso.