Capítulo 5 Modelos no lineales

5.1 Ejemplos

5.1.1 Crecimiento de pavos

Considere los datos de crecimiento de pavos (data(turk0)) de la librería alr4. A 60 corrales de pavos se les alimentó con una dieta similar, complementada con dosis de metionina diferente. Luego de un tiempo determnado, se observó el peso ganado por cada corral.

Las variables son:

• A: Cantidad de suplemento de metionina ( % de la dieta).
• Gain: Peso medio ganado por corral (gramos) después de 3 semanas.

El objetivo del estudio es evaluar la metionina como suplemento alimenticio para pavos. En la Figura 5.1 podemos observar que hay una relación positiva, a mayor cantidad de metionina, mayor peso ganado. Sin embargo, la relación no es lineal. Por lo que sería necesario hacer transformaciones sobre las variables o considerar modelos polinomiales para ajustar un modelo lineal a los datos. Otra alternativa es considerar modelos no lineales.

plot(Gain~A,data=turk0,xlab='cantidad de metionina (% dieta)',ylab='Peso ganado por corral (gramos)')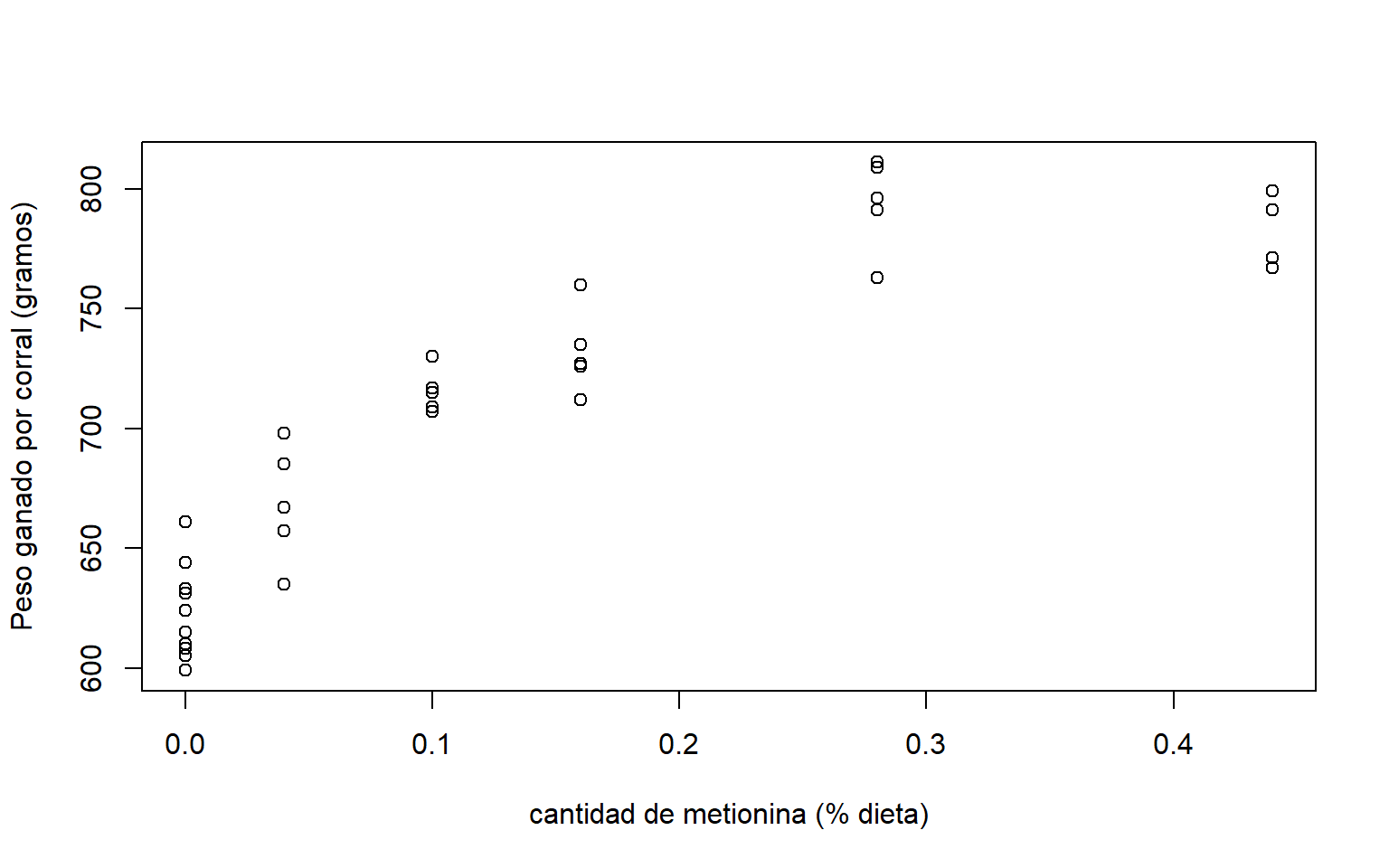

Figure 5.1: Datos de crecimiento de pavos. Relación entre el peso ganado por corral y el % de metionina en la dieta.

Para estos datos se puede considerar el siguiente modelo de crecimiento para la media: \[ E(Gain|A)=\theta_{1}+\theta_{2}[1-exp(-\theta_{3}A)]. \] Dado que este modelo no es una combinación lineal de los parámetros, \(\boldsymbol \theta= (\theta_1,\theta_2,\theta_3)\), se considera como un modelo lineal. Este modelo es comunmente utilizado para ajustar crecimiento dado que sus parámetros tienen interpretación:

• Si \(A=0\), entonces \(E(Gain|A)=\theta_{1}\). Es decir, \(\theta_{1}\) determina el peso ganado medio sin suplemento de metionina.
• Si \(\theta_{3}>0\), \(\theta_{1}+\theta_{2}\) es la asíntota. Es decir, la ganancia máxima de peso que se puede lograr.
• \(\theta_{2}\) es el máximo crecimiento adicional debido al suplemento.
• \(\theta_{3}\) representa la tasa de crecimiento. A valores de \(\theta_3\) mas grandes, el crecimiento esperado se acerca a su máximo más rápidamente.

5.1.2 Puromicina

Los datos Puromycin de la librería datasets contienen información de la reacción enzimática (qué tan rápido ésta cataliza la reacción que convierte un sustrato en producto) de 23 encimas, donde 12 de ellas fueron tratadas con Puromicina (un antibiótico). Las variables son:

• conc :concentración de sustrato (ppm).
• rate:velocidad de reacción instantáneas (conteo/min2)
• state:tratado y no tratado.

El objetivo es evaluar la velocidad de reacción y el efecto de la Puromicina. La relación de la velocidad de reacción en función de la concentración de sustraro se puede observar en la Figura 5.2.

plot(Puromycin$conc,Puromycin$rate,col=Puromycin$state,
     xlab='concentración de sustrato (ppm)',
     ylab='velocidad de reacción')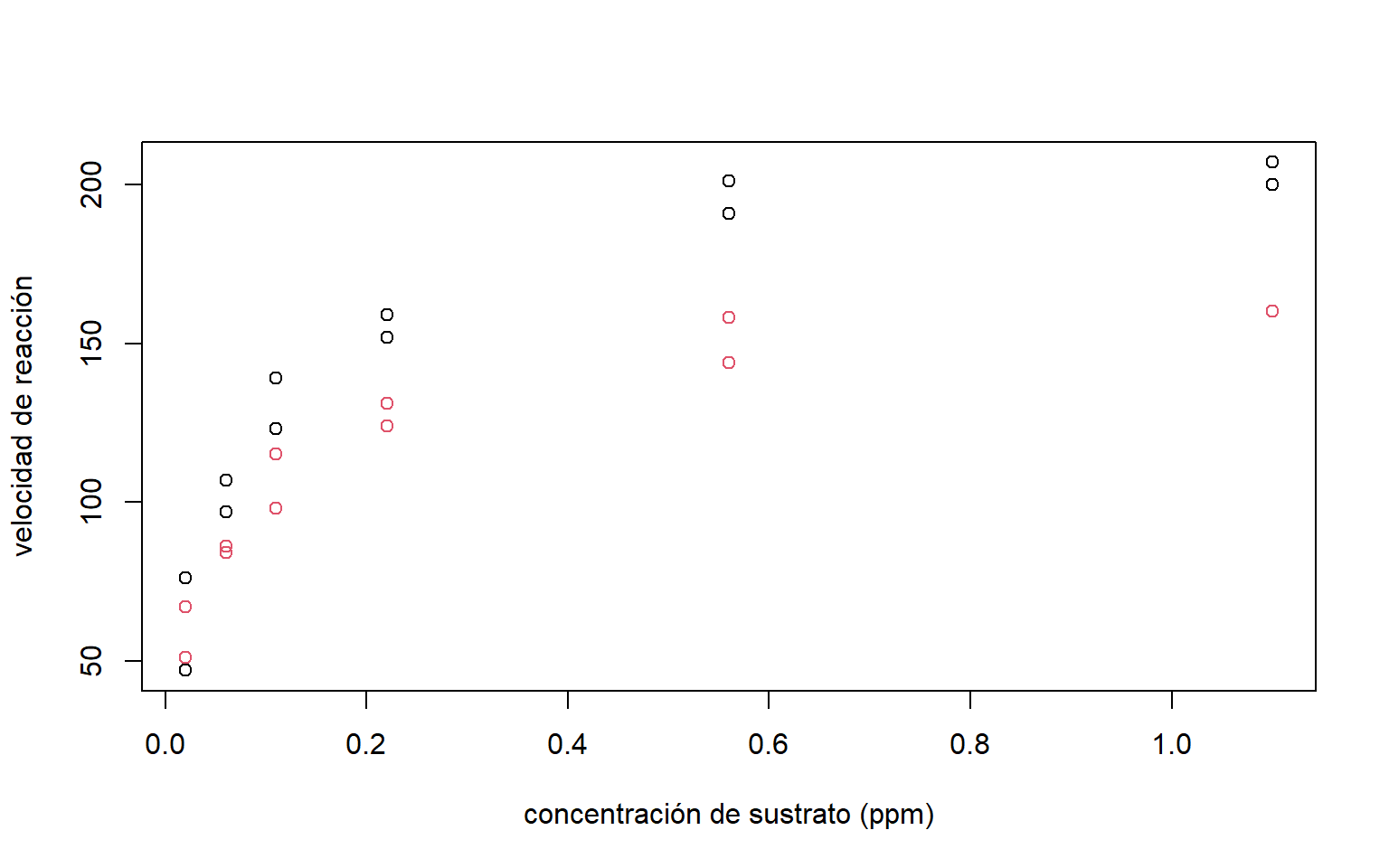

Figure 5.2: Datos de Puromicina. Diagrama de dispersión: Relación entre la velocidad de reacción y la concentración de sustrato. Encimas tratadas(puntos negros), Encimas no tratadas(puntos rojos)

Aquí vamos a considerar el modelo Michaelis-Menten (modelo comunmente utilizado en bioquímica) para la media:

\[ E(y | x )=\frac{x_{1}\theta_{1}}{\theta_{2}+x_{1}}. \] En este caso, \(\theta_1\) es la asíntota. Es decir la velocidad de reacción máxima. Mientras que \(\theta_2\) determina la concentración en la cual se obtiene la mitad de la velocidad máxima. Esto lo podemos observar en la Figura 5.3.

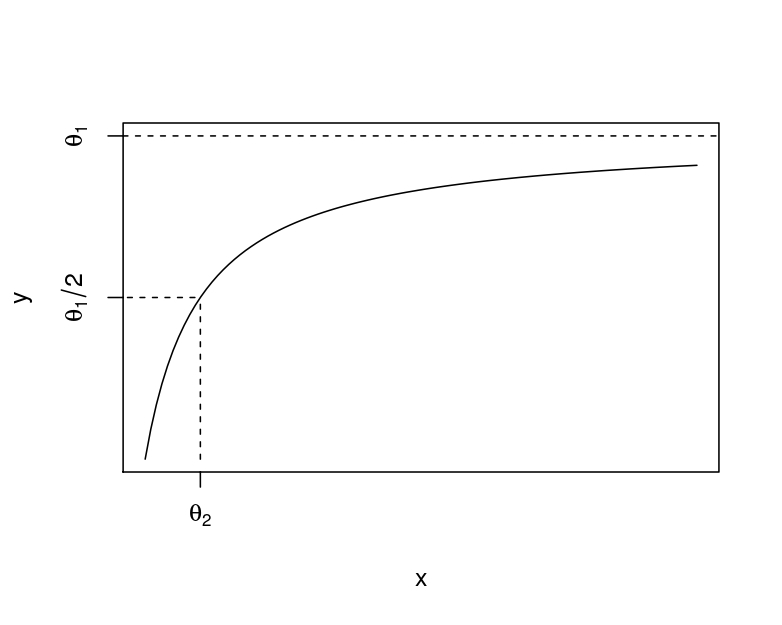
Figure 5.3: Modelo Michaelis-Menten

Dado que se tienen células tratadas y no tratadas, se propone el siguiente modelo para la media: \[ E(\mbox{rate} | \mbox{conc},\mbox{state})=\frac{\mbox{conc}\theta_{1}+\mbox{state}\times \mbox{conc}\theta_{3}} {\theta_{2}+\mbox{state}\theta_{3}+\mbox{conc}}. \] Por lo que se tiene una curva diferente para las enzimas tratadas y no tratadas. Para las primeras la meida es: \[ E(\mbox{rate}|\mbox{conc},\mbox{state}=0)=\frac{\mbox{conc}\theta_{1}}{\theta_{2}+\mbox{conc}}. \] Mientras que, para las segundas la media está dada por: \[ E(\mbox{rate}|\mbox{conc},\mbox{state}=1)=\frac{\mbox{conc}(\theta_{1}+\theta_{3})}{(\theta_{2}+\theta_{4})+\mbox{conc}}. \] De aquí, \(\theta_3\) determina la velocidad máxima entre las células tratadas y no las no tratadas. De igual forma, \(\theta_{4}\) indica la diferencia en la concentración en la cual se obtiene la mitad de la velocidad máxima.

5.2 Modelos no lineales

De forma general, en los modelos de regresión asumimos que:

\[ y_{i}=m(\boldsymbol x_{i},\boldsymbol \theta)+\varepsilon_{i}, \] donde \(\varepsilon_{i} \sim N(0, \sigma^2)\) y \(cov(\varepsilon_{i},\varepsilon_{j}) = 0\), para todo \(i \neq j\). Particularmente, en el caso de modelos lineales, se asume que: \[ m(x_{i},\theta)=\boldsymbol x_i^{*'}\boldsymbol \beta= \beta_{0}+x_{1i}^{*}\beta_{1}+x_{2i}^{*}\beta_{2}+\ldots +x_{p-1,i}^{*}\beta_{p-1}, \] donde \(x_j^{*}\) representa cualquier transformación de las covariables originales, por ejemplo, \(x_j^{*}= \log x_j\) o \(x_j^{*}= x_j^{2}\). Estos modelos se consideran lineales porque son combinaciones lineales de los parámetros \(\boldsymbol \beta\).

Modelos de la forma: \[ y_{i}=m(x_{i},\theta)+\varepsilon_{i}=\theta_{1}+\theta_{1}[1+exp(-\theta_{3}x_{i})]+\varepsilon_{i}, \] o \[ y_{i}=m(x_{i},\theta)+\varepsilon_{i}=\frac{x_{i}\theta_{i}}{\theta_{2}+x_{i}}+\varepsilon_{i}, \] son ejemplos de modelos no lineales. Es decir, no son combinación lineal de los parámetros.

5.2.1 Modelos no-lineales linealizables

Dentro de los modelos no lineales se encuentran algunos que pueden ser linealizables a través de transformaciones sobre las variables. Por ejemplo, el modelo de regresión exponencial: \[ E(y)=\theta_{0}+\theta_{1}\exp(\theta_{2}+x_{i}\theta_{3}), \]

Si \(\theta_{0}=0\), es linealizable: \[ \log y_{i}=(\log\theta_{1}+\theta_{2})+x_{i}\theta_{3}+\varepsilon_{i}^* = \beta_0+x_{i}\beta_1+\varepsilon_{i}^*. \]

5.2.2 Estimación de los parámetros

Al igual que en los modelos lineales, la estimación de \(\boldsymbol \theta\) se hace minimizando la suma de cuadrados de los residuos: \[ S(\boldsymbol \theta)=\sum_{i=1}^n[y_{i}-m(\boldsymbol x_{i},\boldsymbol \theta)]^2. \] Por lo que, para encontrar el mínimo, primero calculamos la derivada de \(S(\boldsymbol \theta)\) con respecto a \(\boldsymbol \theta\): \[ \frac{\partial}{\partial\boldsymbol \theta}S(\boldsymbol \theta)=-2\sum_{i=1}^n[y_{i}-m(\boldsymbol x_{i},\boldsymbol \theta)] \begin{bmatrix}\frac{\partial }{\partial\boldsymbol \theta}m(\boldsymbol x_{i},\boldsymbol \theta)\end{bmatrix}, \] luego igualamos a \(0\), y finalmente, resolvemos la ecuación para \(\boldsymbol \theta\). Sin embargo, en la mayoría de los casos, \(\frac{\partial}{\partial\boldsymbol \theta}S(\boldsymbol \theta)\) es una función no-lineal \(\boldsymbol \theta\). Por lo que no es posible encontrar una solución analítica y necesitamos encontrarla de forma iterativa.

Las técnicas iterativas de estimación de los parámetros están basadas en expansiones de series de Taylor. Cualquier función \(f(\theta)\) puede expandirse como una serie de Taylor de la forma: \[ f(\theta)=\sum_{n=0}^\infty \frac{1}{n!}(\theta-\theta^*)^n \frac{\partial^nf(\theta^*)}{\partial\theta^n}. \] Una aproximación de la función \(f(\theta)\) en los valores alrededor del punto \(\theta^*\) se puede hacer usando series de Taylor de orden dos. Esto es: \[ f(\theta)\approx f(\theta^*)+(\theta-\theta^*) \frac{\partial f(\theta^*)}{\partial\theta}+\frac{1}{2}(\theta-\theta^*)^2\frac{\partial^2 f(\theta^*)}{\partial\theta^2}. \] En caso de que \(\boldsymbol \theta\) sea un vector de dimensión \(p\), la aproximación por series de Taylor de orden dos se expresa de la siguiente manera: \[ f(\boldsymbol \theta)\approx f(\boldsymbol \theta^*)+(\boldsymbol \theta-\boldsymbol \theta^*)^{'}u(\boldsymbol \theta^*)+\frac{1}{2}(\boldsymbol \theta-\boldsymbol \theta^*)^{'}H(\boldsymbol \theta^*)(\boldsymbol \theta-\boldsymbol \theta^*), \] donde: \[ u(\boldsymbol \theta)=\frac{\partial S(\boldsymbol \theta)}{\partial\boldsymbol \theta}=\begin{pmatrix} \frac{\partial S(\boldsymbol \theta)}{\partial\theta_1} \\ \frac{\partial S(\boldsymbol \theta)}{\partial\theta_2} \\ \vdots \\ \frac{\partial S(\boldsymbol \theta)}{\partial\theta_p} \\ \end{pmatrix} \qquad u(\widehat{\boldsymbol \theta})=u(\boldsymbol \theta)|_{\boldsymbol \theta=\widehat{\boldsymbol \theta}}, \] es el vector score, y \[ \boldsymbol H(\boldsymbol \theta)= \frac{\partial^2 S(\boldsymbol \theta)}{\partial\boldsymbol \theta^{'} \partial\boldsymbol \theta}=\begin{pmatrix} \frac{\partial^2 S(\boldsymbol \theta)}{\partial^2 \theta_{1}} & \frac{\partial^2 S(\boldsymbol \theta)}{\partial \theta_{1} \partial \theta_{2} } & \dots & \frac{\partial^2 S(\boldsymbol \theta)}{\partial \theta_{1} \partial \theta_{p}} \\ \frac{\partial^2 S(\boldsymbol \theta)}{\partial \theta_{2} \partial \theta_{1}} & \frac{\partial^2 S(\boldsymbol \theta)}{\partial^2 \theta_{2}} & \dots & \frac{\partial^2 S(\boldsymbol \theta)}{\partial \theta_{2} \partial \theta_{p}}\\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 S(\boldsymbol \theta)}{\partial \theta_{p} \partial \theta_{1}} & \frac{\partial^2 S(\boldsymbol \theta)}{\partial \theta_{p} \partial \theta_{2}} & \dots & \frac{\partial^2 S(\boldsymbol \theta)}{\partial^2 \theta_{p}} \end{pmatrix} \quad \quad \quad \boldsymbol H(\widehat{\boldsymbol \theta})=\boldsymbol H(\boldsymbol \theta)|_{\boldsymbol \theta=\widehat{\boldsymbol \theta}}, \] es la matriz hessiana.

Algunos métodos iterativos de estimación son: Gauss-Newton (aproximación de series de Taylor a la función de la media) y Newton-Raphson (aproximación de series de Taylor a la función score). Para ajustar modelos ni lineales, generalmente, se opta por la primera.

La idea es aproximar \(m(x_{i},\boldsymbol \theta^*)\) usando series de Taylor de orden uno alrededor de \(\boldsymbol \theta^*\), esto es:

\[\begin{equation} m(x_{i},\boldsymbol \theta)\approx m(x_{i},\boldsymbol \theta^*)+(\boldsymbol \theta-\boldsymbol \theta^*)^{'}u_{i}(\boldsymbol \theta^*). \tag{4.1} \end{equation}\]

Note que (4.1) tiene la forma de un modelo lineal, donde \(u_{i}(\boldsymbol \theta^*)\) juega el papel de vector de covariables. La diferencia radica en que \(u_{i}(\boldsymbol \theta^*)\) puede depender de los parámetros.

La aproximación de la suma de cuadrados de los residuos es: \[\begin{equation} \begin{split} S(\boldsymbol \theta)&=\sum_{i=1}^n[y_{i}-m(x_{i},\boldsymbol \theta)]^2 \approx \sum_{i=1}^n[y_{i}-m(x_{i},\boldsymbol \theta^*)+(\boldsymbol \theta-\boldsymbol \theta^*)^{'}u_{i}(\boldsymbol \theta^*)]^2 \\ &= \sum_{i=1}^n[\widehat e_{i}^*+(\boldsymbol \theta-\boldsymbol \theta^*)^{'}u_{i}(\boldsymbol \theta^*)]^2. \end{split} \nonumber \end{equation}\]

Esta aproximación de \(S(\boldsymbol \theta)\) es equivalente a una suma de cuadrados de un modelo lineal con \(\widehat e_{i}^*\) (llamados residuos de trabajo) como variable respuesta y \(u_{i}(\boldsymbol \theta^*)\) como vector de covariables. Por lo tanto, la solución es: \[ (\widehat{\boldsymbol \theta}-\boldsymbol \theta^*)=[U(\boldsymbol \theta^*)^{'}U(\boldsymbol \theta^*)]^{-1}U(\boldsymbol \theta^*)^{'} \widehat e^*, \] \[\begin{equation} \hat{\boldsymbol \theta}=\boldsymbol \theta^*+[U(\boldsymbol \theta^*)^{'}U(\boldsymbol \theta^*)]^{-1}U(\boldsymbol \theta^*)^{'} \widehat e^*, \tag{5.1} \end{equation}\]

donde \(\widehat e_{i}^*=(\widehat e_{1}^*,\ldots,\widehat e_{n}^*)^{'}\), \(U(\boldsymbol \theta^*)\) es una matriz con la \(i\)-ésima fila igual a \(u_{i}(\boldsymbol \theta^*)\).

A partir de estas ecuaciones se propone el siguiente algoritmo (de Gauss-Newton):

1. seleccione unos valores iniciales \(\boldsymbol \theta_{0}\) y calcule \(S(\boldsymbol \theta_{0})\),

2. establezca el contador de iteraciones en \(j=0\),

3. calcule \(U(\boldsymbol \theta^{(j)})\) y \(\widehat e^{(j)}\) y encuentre \(\boldsymbol \theta^{(j+1)}\) usando (5.1). Esto es: \[\begin{equation} \begin{split} & \boldsymbol \theta^{(j+1)}=\boldsymbol \theta^{(j)}+[U(\boldsymbol \theta^{(j)})^{'}U(\boldsymbol \theta^{(j)})]^{-1}U(\boldsymbol \theta^{(j)})^{'} \widehat e^{(j)}, \end{split} \end{equation}\] y calcule \(S(\boldsymbol \theta^{(j+1)})\).

4. Pare si \(\delta=|S(\boldsymbol \theta^{(j)})-S(\boldsymbol \theta^{(j+1)})|\) es suficientemente pequeño (convergencia). De otra forma, \(j=j+1\) y vaya al paso 3.

Si hay demasiadas iteraciones (\(j\) es muy grande), se dice que hay divergencia.

La estimación de \(\sigma^2\) es:

\[ \widehat{\sigma}^2=\frac{1}{n-p}\sum_{i=1}^n[y_{i}-m(\boldsymbol x_{i},\widehat{\boldsymbol \theta})]^2. \] Todos los métodos iterativos de selección requieren de la selección de valores iniciales. Para evitar problemas de divergencia, es preferible escoger valores que estén cercanos a los parámetros. Esto se puede lograr basándose en conocimiento previo del problema, significado físico de los coeficientes, evaluación gráfica o linealización de los datos. Otro aspecto que se debe tener en cuenta es que este tipo de algoritmos pueden caer en un máximo local. Por lo que es recomendable ejecutar el algoritmo para diferentes valores iniciales.

En el caso del peso de los pavos, se pueden utilizar los siguientes valores iniciales:

• \(\theta_{1}^0=620\) (promedio del peso ganado sin suplemento).

• \(\theta_{2}^0+\theta_{1}^0=800\) (valor cercano al máximo peso obtenido). Por lo tanto \(\theta_{2}^0=180\)

• \(\theta_{3}^0\) se puede obtener resolviendo la siguiente ecuación \(E(y) = \theta_1^{0}+\theta_2^{0}[1-\exp(-\theta_{3} A)]\) para un posible punto. Por ejemplo, si \(A=0.16\), un valor posible para \(E(y)\) es 750. Por lo que: \[ 750=620+180[1-\exp(-\theta_{3}^00.16)]. \] Resolviendo la ecuación \(\theta_{3}^0\approx8\).

En R, la estimación del modelo lineal se hace usando la función ´nls()´. Para el caso de crecimiento de los pavos:

mod.turk = nls(Gain ~ th1 + th2*(1-exp(-th3*A)),data = turk0,
          start = list(th1=620,th2=180,th3=8),trace=F)
mod.turk

## Nonlinear regression model
##   model: Gain ~ th1 + th2 * (1 - exp(-th3 * A))
##    data: turk0
##     th1     th2     th3 
## 622.958 178.252   7.122 
##  residual sum-of-squares: 12367
## 
## Number of iterations to convergence: 4 
## Achieved convergence tolerance: 6.719e-06

Por lo que la estimación de la media del peso ganado por corral es: \[ E(\mbox{Gain}|A)=622.958 + 178.252 [1 - \exp(-7.122A)]. \] La figura 5.4 muestra el ajuste de forma gráfica.

plot(Gain~A,data=turk0,xlab='cantidad de metionina (% dieta)',ylab='Peso ganado (gramos)')
th.turk = coef(mod.turk)
x = seq(0,0.5,length.out=100)
lines(x, th.turk[1]+th.turk[2]*(1-exp(-th.turk[3]*x)),col=2, lwd = 2)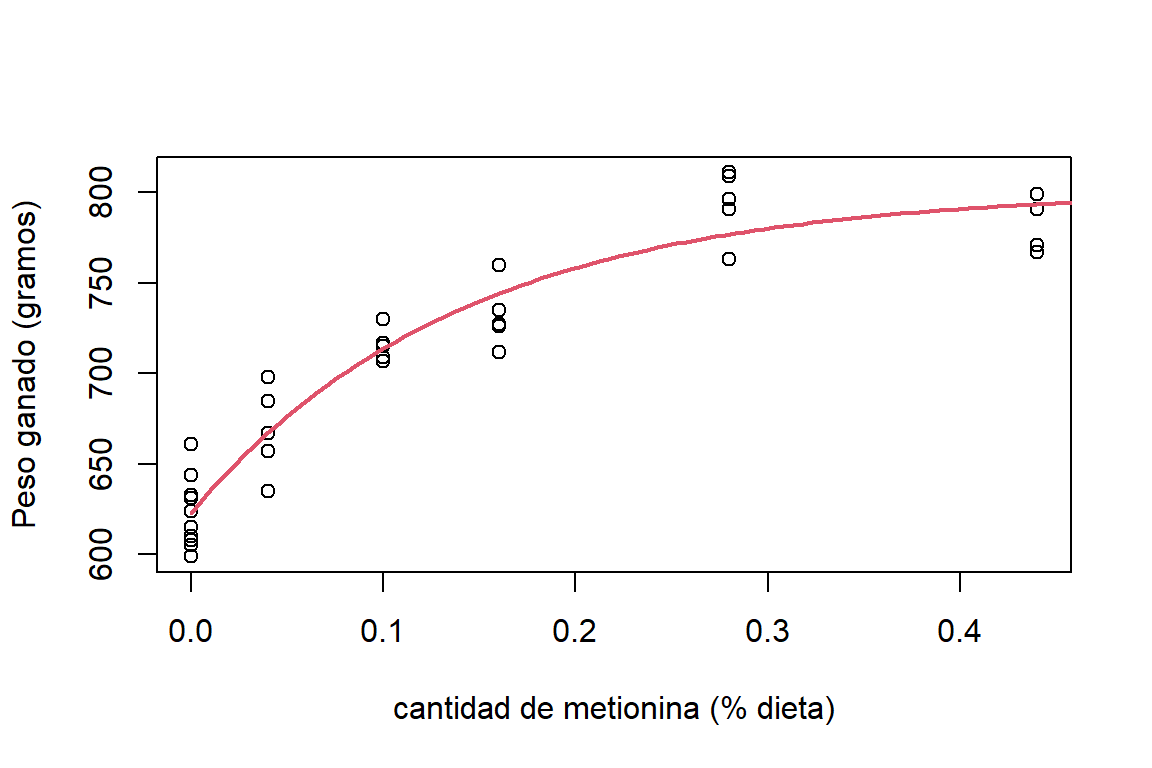

Figure 5.4: Datos de crecimiento de pavos. Ajuste del modelo para el peso medio ganado por corral en función de la cantidad de suplemento de metionina.

5.2.3 Inferencia sobre los parámetros

Las propiedades del \(\widehat{\boldsymbol \theta}\) se basan en teoría asintótica, es decir que son válidas si se tiene muestras grandes. Si \(\varepsilon \sim N(\boldsymbol 0,\sigma^2 \boldsymbol I)\), tenemos que asintóticamente \((n \to \infty)\):

\[ \widehat{\boldsymbol \theta}\sim N\left(\boldsymbol \theta,\sigma^2\left[U(\boldsymbol \theta^*)U(\boldsymbol \theta^*)'\right]^{-1}\right). \] Esto quiere decir que, \(\widehat{\boldsymbol \theta}\) es un estimador asintoticamente insesgado de \(\boldsymbol \theta\) y se distribuye de forma normal. Además, se puede probar que es un estimador eficiente (es decir, de mínima varianza).

A partir de estos resultados se pueden hacer inferencias sobre los coeficientes \(\boldsymbol \theta\). Por ejemplo, pruebas de hipótesis sobre algún coeficiente \(\theta_j\) del modelo: \[ \qquad H_{0}:\theta_{j}=\theta_{0}, \qquad H_{1}:\theta_{j}\ne\theta_{0}, \] se puede hacer a través del siguiente estadístico de prueba: \[ t_{0}:\frac{\widehat{\theta_{j}}-\theta_{0}}{\sqrt{V(\widehat{\theta_{j}})}}, \quad \text{donde} \quad t_{0} \sim t_{n-p}. \] También, para pruebas de hipótesis sobre un subconjuntos de parámetros de \(\boldsymbol \theta=(\boldsymbol \theta_{1}^{'},\boldsymbol \theta_{2}^{'})^{'}\): \[ H_{0}:\boldsymbol \theta_{2}=\boldsymbol 0\qquad H_{1}:\boldsymbol \theta_{2}\ne\boldsymbol 0, \] el estadístico de prueba que se utiliza es: \[ F_{0}=\frac{[SS_{res}(\boldsymbol \theta)-SS_{res}(\boldsymbol \theta_{1})]/r}{MS_{res}(\boldsymbol \theta)}\sim F_{r,n-p}. \] De igual forma, la estimación por intervalos del \((1-\alpha)\)% de confianza para \(\theta_{j}\) se puede calcular como:

\[ \hat{\theta_{j}}\pm t_{1-\alpha/2,n-p}\sqrt{V(\hat{\theta_{j}})} , \] Con la función confint de R se pueden obtener los IC de los coeficientes a través de los perfiles de verosimilitud.

Hay que hacer énfasis que estas son propiedades para muestras grandes, para muestras pequeñas, estas propiedades pueden ser inadecuadas y se puede recurrir a otras alternativas, como el bootstrap.

Para el modelo de crecimiento de los pavos, tenemos que:

summary(mod.turk)

## 
## Formula: Gain ~ th1 + th2 * (1 - exp(-th3 * A))
## 
## Parameters:
##     Estimate Std. Error t value Pr(>|t|)    
## th1  622.958      5.901  105.57  < 2e-16 ***
## th2  178.252     11.636   15.32 2.74e-16 ***
## th3    7.122      1.205    5.91 1.41e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 19.66 on 32 degrees of freedom
## 
## Number of iterations to convergence: 4 
## Achieved convergence tolerance: 6.719e-06

A partir de este ajuste se puede concluir que el peso medio obtenido sin suplemento es de \(622\). Mientras que la ganancia máxima que se obtiene con el suplemento es de \(178\). A partir de las pruebas \(t\) se puede determinar que la ganancia máxima es significativamente mayor que cero. Los intervalos de confianza para \(\boldsymbol \theta\) se obtienen de la siguiente forma:

confint(mod.turk)

## Waiting for profiling to be done...

##           2.5%      97.5%
## th1 610.970918 634.855196
## th2 156.322676 204.476710
## th3   4.966356   9.777723

Aquí podemos ver que, por ejemplo, la ganancia máxima que se puede obtener con el suplemento está entre \(156\) y \(204\) gramos con un nivel de confianza del 95%.

Para calcular los intervalos de confianza para la media podemos utilizar la función predFit de la librería investr. La Figura 5.5 muestra el intervalo del 95% del peso ganado medio en función del % de metionina en la dieta.

library(investr)
predx = data.frame(A=seq(from=0,to=0.5,length.out=100))

predGain = predFit(mod.turk,predx,interval='confidence')

plot(Gain~A,data=turk0,xlab='cantidad de metionina (% dieta)',ylab='Peso ganado (gramos)')
th = coef(mod.turk)
x = seq(0,0.5,length.out=100)
lines(x, th.turk[1]+th.turk[2]*(1-exp(-th.turk[3]*x)),col=2, lwd = 2)
lines(predx$A,predGain[,2],col=2,lty=2,lwd=2)
lines(predx$A,predGain[,3],col=2,lty=2,lwd=2)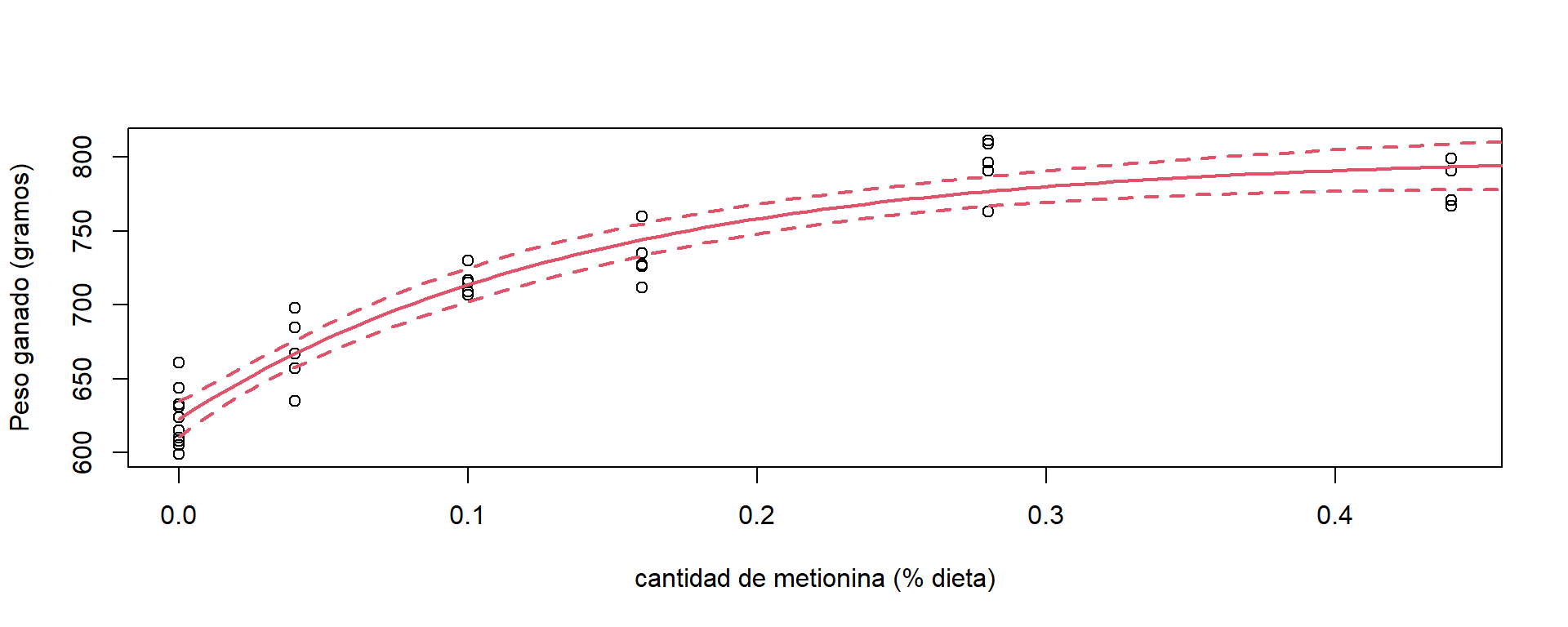

Figure 5.5: Datos pavos. Intervalo del 95% de confianza para la media del peso ganado en función de la dieta.

Es posible considerar otros modelos de crecimiento para este conjunto de datos. Algunos de estos son el modelo logístico: \[ y_{i}=\frac{\theta_{1}}{1+\theta_{2}\exp(-\theta_{3}x_{i})}+\varepsilon_{i}, \] o el modelo Weibull:

\[ y_{i}=\theta_{1}+\theta_{2}[1-\exp(-\theta_{3}x_{i}^{\theta_{4}})]+\varepsilon_{i}. \] Para compararlos, podemos ajustarlos y verificar cuál de los tres proporciona mejor ajuste usando criterios de información (AIC o BIC). En la Figura 5.6, y a través del BIC, podemos ver que los tres modelos proporcionan casi el mismo ajuste. Así que, cualquiera puede ser usado para hacer inferencias y sacar conclusiones.

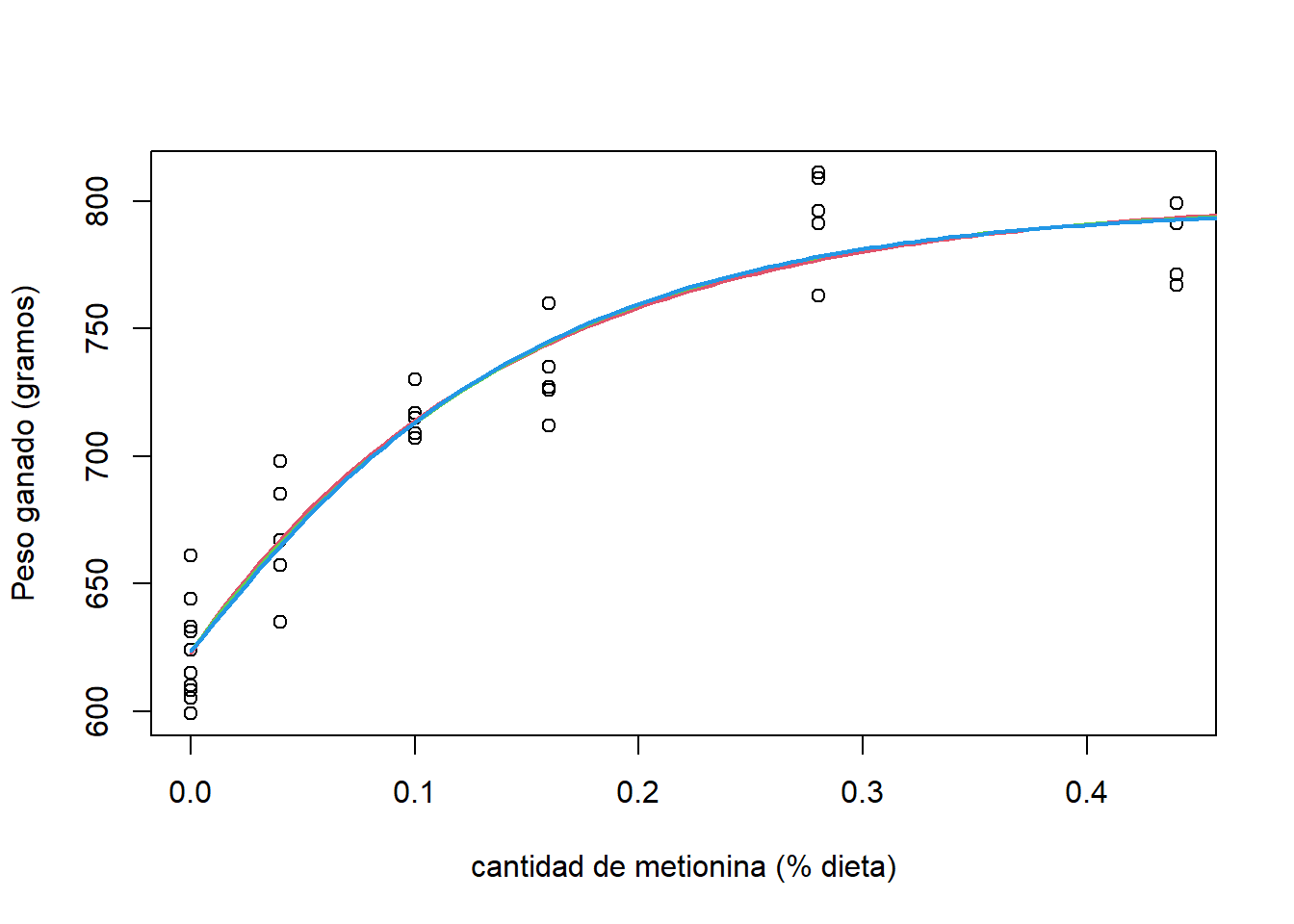
Figure 5.6: Datos de crecimiento de pavos. Ajuste del modelo de crecimiento propuesto (rojo), modelo logístico (verde) y Modelo Weibull (azul).

## [1] 318.9086

## [1] 318.6193

## [1] 322.3054

5.2.3.1 Puromicina-Estimación

Los valores iniciales del modelo Michaelis-Menten se puede hacer por linealización. Tenemos que: \[ m(\boldsymbol x,\boldsymbol \theta) = \frac{\theta_1 x}{x + \theta_2}, \] es linealizable aplicando la inversa a ambos lados de la ecuación: \[ \frac{1}{m(\boldsymbol x,\boldsymbol \theta)} = \frac{x + \theta_2}{\theta_1 x} = \frac{1}{\theta_1} + \frac{1}{x}\frac{\theta_2}{\theta_1}. \] En la Figura 5.7 podemos ver que aplicando inversas a ambas variables se obtiene una relación aproximadamente lineal.

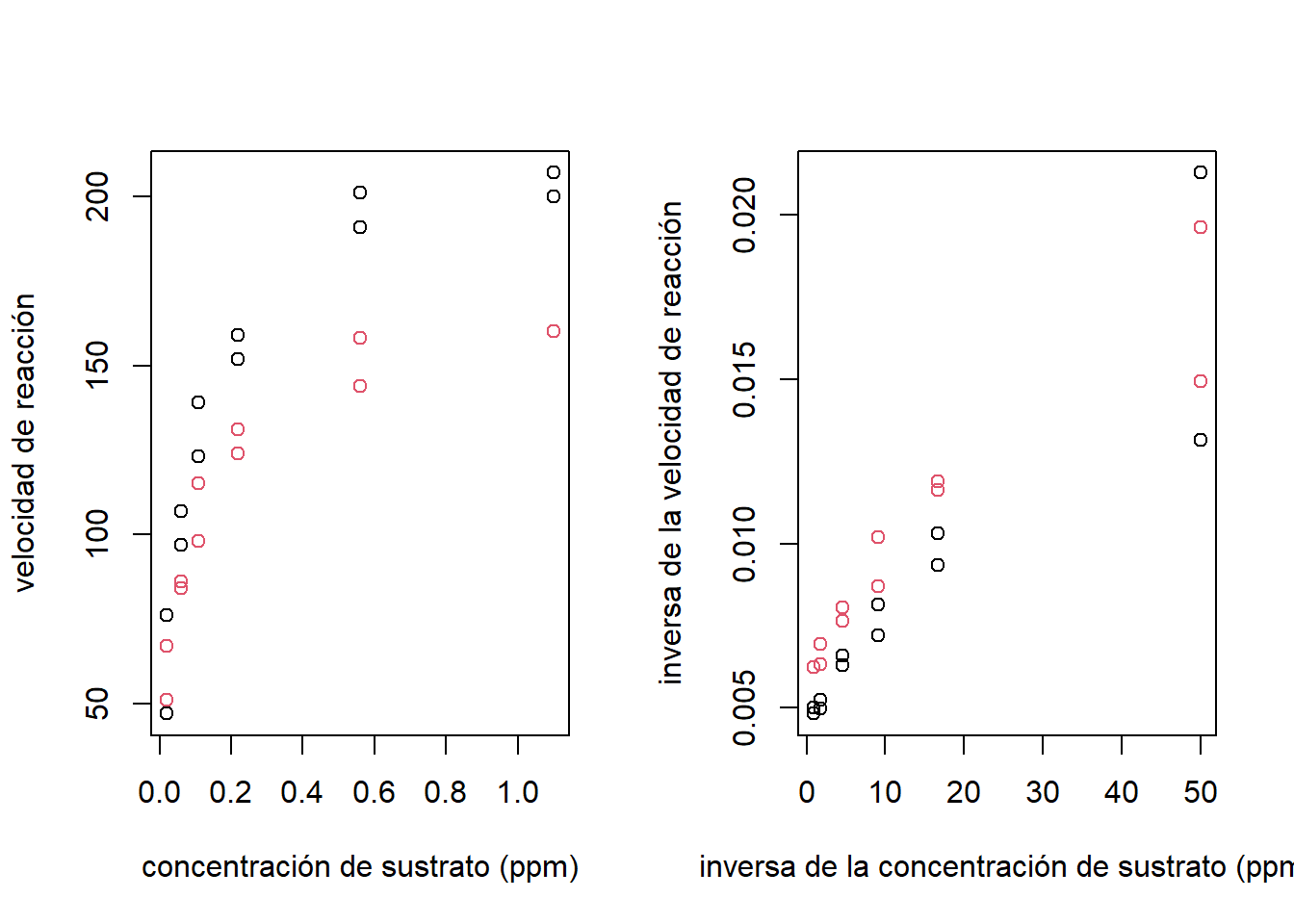
Figure 5.7: Datos de puromicina. Diagrama de dispersión. Datos linealizados(derecha).

A través del ajuste por MCO para:

\[ 1/y_{i}=\beta_{0}+1/\mbox{conc}_{i}\beta_{1}+\varepsilon_{i}, \] se puede obtener valores iniciales. Luego de ajustar el modelo se obtiene que:

\[ \theta_{1}^{(0)}=\frac{1}{\hat{\beta}_{0}}=167.408 \mbox{ y } \theta_{2}^{(0)}=\frac{\hat{\beta}_{1}}{\hat{\beta}_{0}}=0.039. \] Inicialmente, se podríamos asumir que \(\beta_{3}^{(0)}=\beta_{4}^{(0)}=0\) (es decir, no hay diferencias entre las células tratadas y no tratadas). Usando la función ´nls()´ de R obtenemos los siguientes resultados:

Puromycin$state2 = as.double(Puromycin$state == 'treated')
mod.puromicyn = nls(rate ~ (th1*conc + th3*conc*state2)/(th2+th4*state2+conc),data = Puromycin,
          start = list(th1=168,th2=0.4,th3=0,th4=0),trace=F )
summary(mod.puromicyn )

## 
## Formula: rate ~ (th1 * conc + th3 * conc * state2)/(th2 + th4 * state2 + 
##     conc)
## 
## Parameters:
##      Estimate Std. Error t value Pr(>|t|)    
## th1 1.603e+02  6.896e+00  23.242 2.04e-15 ***
## th2 4.771e-02  8.281e-03   5.761 1.50e-05 ***
## th3 5.240e+01  9.551e+00   5.487 2.71e-05 ***
## th4 1.641e-02  1.143e-02   1.436    0.167    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.4 on 19 degrees of freedom
## 
## Number of iterations to convergence: 7 
## Achieved convergence tolerance: 3.021e-06

Con estos resultados podemos concluir que la tasa de crecimiento máxima es significativamente diferente si la enzima es tratada o no (\(\theta_3\) es significativamente diferente de cero). Sin embargo, el punto en que se alcanza la mitad del máximo es el mismo (\(\theta_4\) no es significativamente diferente de cero). El ajuste se puede observar de forma gráfica en la Figura 5.8. Las líneas horizontales muestran la diferencia entre las asíntotas entre las céludas tratadas y las no tratadas. Mientras que, las líneas verticales la concentración donde se obtiene la mitad de la velocidad de reacción máxima.

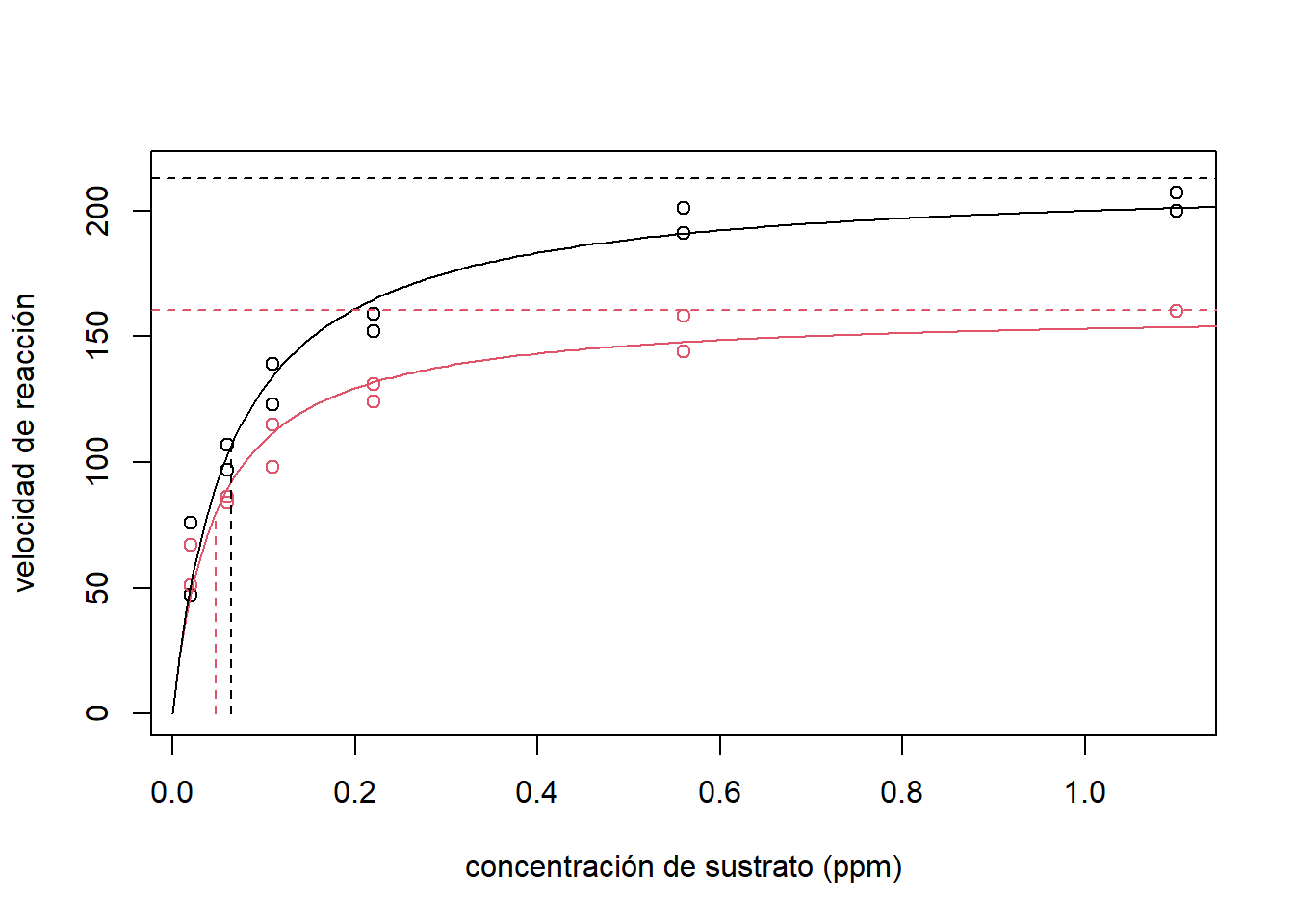
Figure 5.8: Datos de puromicina. Estimación de la velocidad media de reacción para enzimas tratadas(línea negra) y enzimas no tratadas(línea roja).

5.3 Método de Bootstrap

Los métodos de inferencia que se muestran anteriormente se basan en la distribución asintótica de los estimadores. Por lo que pueden ser inexactas y/o engañosas si tenemos muestras pequeñas. En esos casos, una alternativa preferible es usar ténicas de remuestreo (bootstrap).

El bootstrap es una técnica que se puede usar para calcular intervalos de confianza and pruebas de hipótesis cuando el cumplimiento de los supuestos distribucionales asumidos sobre los estimadores están en duda (por ejemplo, normalidad de \(\widehat{\boldsymbol \theta}\)). Por ejemplo, si se quiere calcular un intervalo de confianza para la mediana de \(Y\) no sabemos la distribución del estimador. Por lo tanto, podemos calcularlo utilizando bootstrap. Para esto, seguimos los siguientes pasos:

1. Obtener una muestra aleatoria con remuestreo de \(\boldsymbol y=(y_{1}^{*},...,y_{n}^{*})\),
2. calcular la mediana usando la muestra el paso 1 \((Me_{1}^*)\).
3. repetir los pasos 1 y 2 un número grande de veces \((B)\).

De aquí, la distribución muestral de \(Me\) se obtiene a partir de los remuestreos. Esto es \((Me_{1}^*,\ldots,Me_{B}^*)\). El intervalo de confianza del 95% se puede calcular a partir de los percentiles muestrales 2.5% y 97.5 % de \((Me_{1},\ldots,Me_{B})\).

5.3.1 Bootstrap en regresión

Para un modelo de regresión, el remuestreo se hace sobre los observaciones, considerando la respuesta y las covariables, \((y_i,\boldsymbol x_i)\), o sobre los residuos del ajuste por MCO. El segundo método es llamado residual resampling y se realiza de las siguiente forma:

1. Con la muestra dada, \((x_{i},y_{i}),i=1,...,n\), ajustar el modelo y obtener los residuos: \(e_{i}=y_{i}-x_{i}^{'}\hat{\beta}\),

2. obtener una muestra aleatoria con reemplazo de los residuos, \(e^*=(e_{1}^*,...,e_{n}^*)\),

3.crear una variable respuesta bootstrap \(y_{i}^*=\boldsymbol x_{i}^{'}\widehat{\boldsymbol \beta}+e_{1}^*\) y estimar \(\widehat{\boldsymbol \beta}^*_1\), 4. repetir los pasos 1-3 un número grande de veces \((B)\), 5. obtener el intervalo de confianza para \(\beta_{j}\) usando los percentiles de \((\widehat{\beta}^*_{j,1},\ldots,\widehat{\beta}^*_{j,B})\).

En la literatura se pueden encontrar muchas modificaciones y extensiones para calcular los intervalos de confianza y para realizar el remuestreo.

Para los datos de la Puromicina, el bootstrap en R se puede implementar utilizando la función Boot de la librería car:

set.seed(310)
mod.boot = Boot(mod.puromicyn,method='residual',R=1000)
mod.boot

## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot::boot(data = data.frame(update(object, model = TRUE)$model), 
##     statistic = boot.f, R = R, .fn = f, parallel = p_type, ncpus = ncores, 
##     cl = cl2)
## 
## 
## Bootstrap Statistics :
##         original        bias    std. error
## t1* 160.27996673  8.913060e-01  6.33925160
## t2*   0.04770806 -1.031726e-05  0.00748367
## t3*  52.40375557  8.813317e-02  8.90147827
## t4*   0.01641319 -3.563328e-05  0.01053056

En el objeto mod.boot se pueden observar todas las estimaciones calculadas en los \(1000\) remuestreos. Por ejemplo, la relaciones entre las estimaciones se pueden observar a través de un diagrama de dispersión (Figura 5.9). Aquí vemos una correlaciones altas en algunas de las estimaciones.

pairs(mod.boot$t,labels=c(expression(hat(theta)[1]),expression(hat(theta)[2]),expression(hat(theta)[3]),
                          expression(hat(theta)[4])))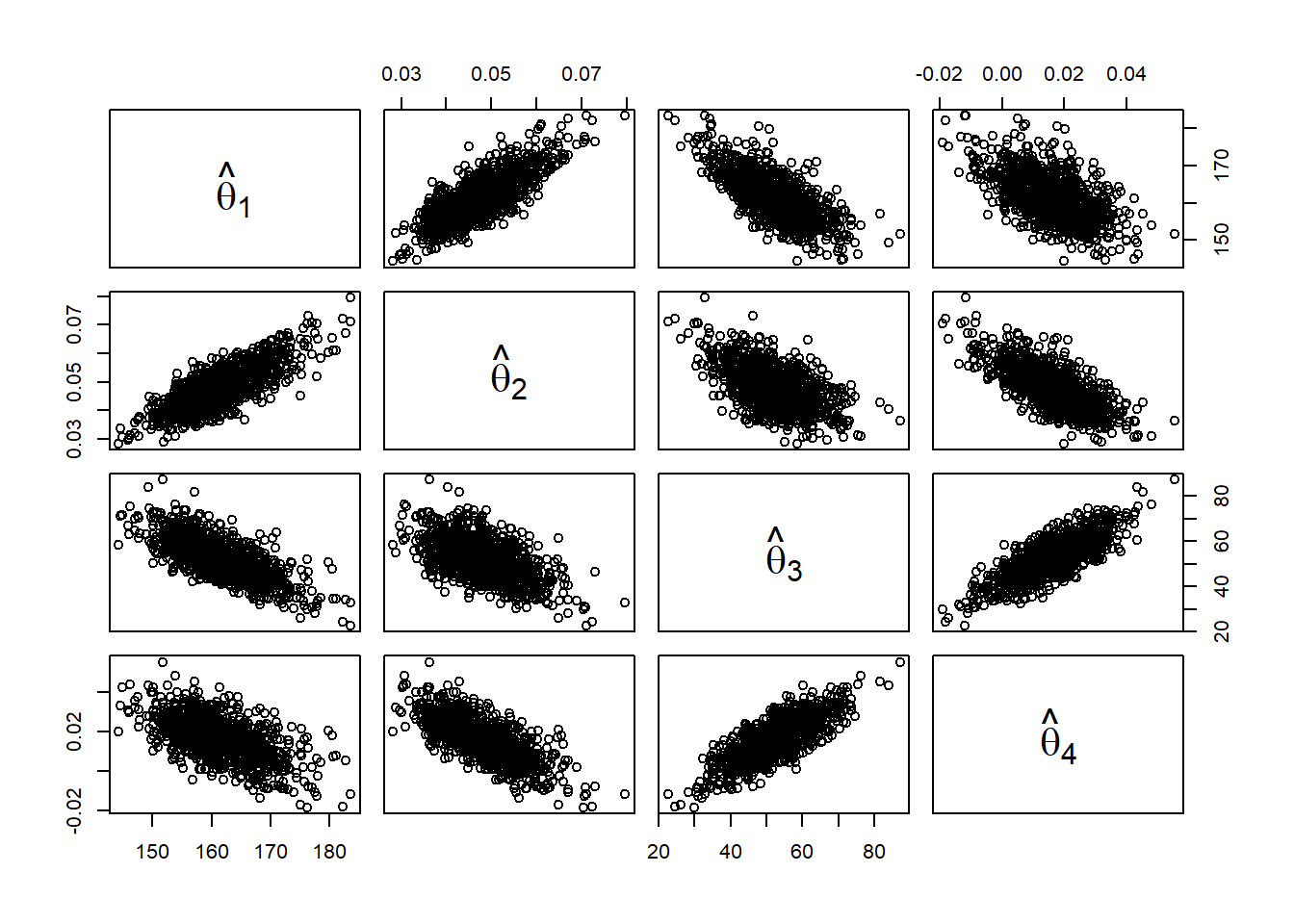

Figure 5.9: Datos de puromicina. Diagrama de dispersión para las estimaciones bootstrap de los coeficientes del modelo.

Igualmente, la distribución muestral de los estimadores de los coeficientes se pueden obtener a partir de histogramas (ver Figura 5.10). Estas parecen aproximarse a distribuciones normales, sin embargo, hay leves asimetrías en \(\widehat{\theta}_1\) y \(\widehat{\theta}_2\).

par(mfrow=c(1,4))
hist(mod.boot$t[,1],breaks = 20,xlab=expression(hat(theta)[1]),main = '')
abline(v=coef(mod.puromicyn)[1],lty=2,lwd=2)
abline(v=mean(mod.boot$t[,1]),lty=2,lwd=2,col=2)
abline(v=quantile(mod.boot$t[,1],c(0.025,0.975),na.rm = T),lty=2,lwd=2,col=2)

hist(mod.boot$t[,2],breaks = 20,xlab=expression(hat(theta)[2]),main = '')
abline(v=coef(mod.puromicyn)[2],lty=2,lwd=2)
abline(v=mean(mod.boot$t[,2]),lty=2,lwd=2,col=2)
abline(v=quantile(mod.boot$t[,2],c(0.025,0.975),na.rm = T),lty=2,lwd=2,col=2)

hist(mod.boot$t[,3],breaks = 20,xlab=expression(theta[3]),main = '')
abline(v=coef(mod.puromicyn)[3],lty=2,lwd=2)
abline(v=mean(mod.boot$t[,3]),lty=2,lwd=2,col=2)
abline(v=quantile(mod.boot$t[,3],c(0.025,0.975),na.rm = T),lty=2,lwd=2,col=2)

hist(mod.boot$t[,4],breaks = 20,xlab=expression(theta[4]),main = '')
abline(v=coef(mod.puromicyn)[4],lty=2,lwd=2)
abline(v=mean(mod.boot$t[,4]),lty=2,lwd=2,col=2)
abline(v=quantile(mod.boot$t[,4],c(0.025,0.975),na.rm = T),lty=2,lwd=2,col=2)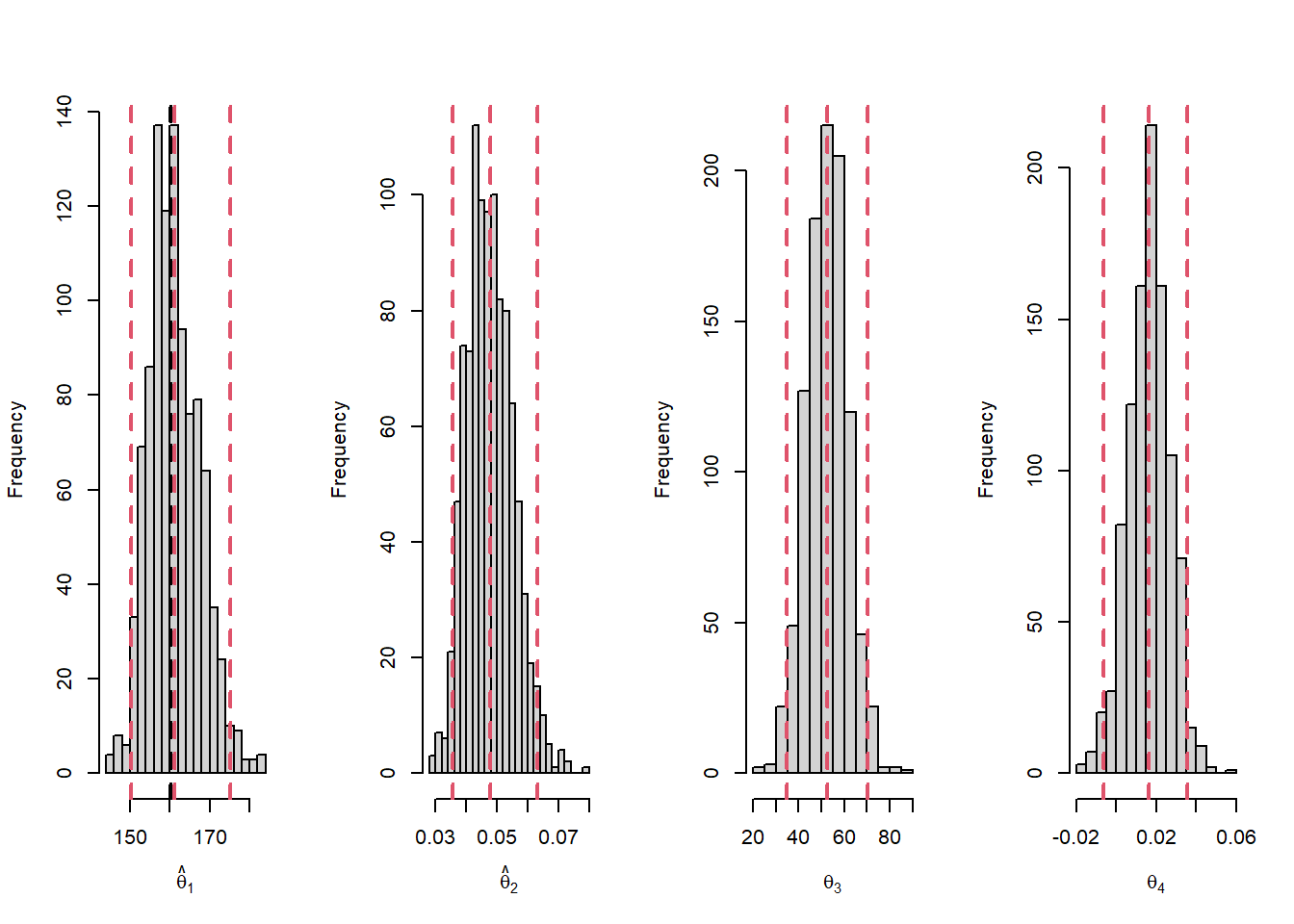

Figure 5.10: Datos de puromicina. Histograma de las estimaciones de los coeficientes del modelo por bootstrap. la linea negra indica la estimación por mínimos cuadrados.La lineas rojas representa los percentiles 2.5 y 97.5 de los remuestreos.

Finalmente, los intervalos del 95% de confianza usando bootstrap se pueden obtener a partir de los percentiles 2.5% y 97.5% de las distribuciones remuestreadas:

quantile(mod.boot$t[,1],c(0.025,0.975),na.rm = T)

##     2.5%    97.5% 
## 150.2787 175.1420

quantile(mod.boot$t[,2],c(0.025,0.975),na.rm = T)

##       2.5%      97.5% 
## 0.03538989 0.06328547

quantile(mod.boot$t[,3],c(0.025,0.975),na.rm = T)

##     2.5%    97.5% 
## 34.81826 70.20826

quantile(mod.boot$t[,4],c(0.025,0.975),na.rm = T)

##         2.5%        97.5% 
## -0.006628693  0.035401146

En la Figura 5.11 se pueden observar todas las estimaciones de la media obtenidas a partir de los 1000 remuestreos. Se puede observar que en todos los casos, la máxima velocidad de obtuvo para las células tratadas.

fit.rate= function(theta,x){
  cbind(theta[1]*x/(theta[2]+x),
        (theta[1]+theta[3])*x/(theta[2]+theta[4]+x))
}
x= seq(from=0,to=1.1,length.out = 100)

plot(NULL,NULL,xlim=c(0,1.1),ylim=c(0,210),xlab='concentración de sustrato (ppm)',
     ylab='velocidad de reacción')
Fit = mapply(function(i){
  pred = fit.rate(mod.boot$t[i,],x)
  lines(x,pred[,1],col='lightgray')
  lines(x,pred[,2],col='gray')
},i=1:999)
lines(x, thP[1]*x/(thP[2]+x),col=2)
lines(x, (thP[1]+thP[3])*x/(thP[2]+thP[4]+x))
points(Puromycin$conc,Puromycin$rate,col=Puromycin$state)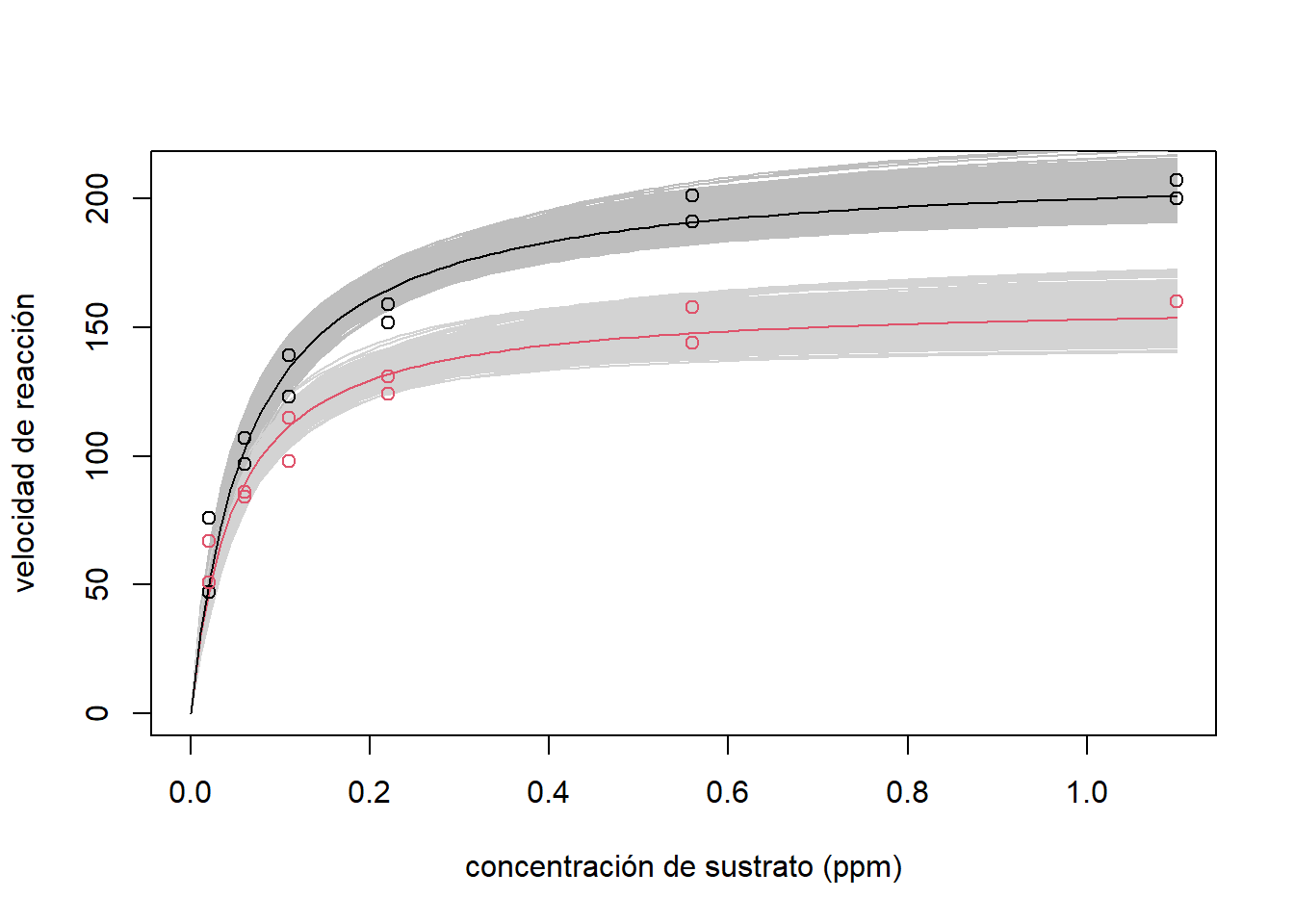

Figure 5.11: Datos de puromicina. Curvas medias estimadas por bootstrap. La estimación puntual de la media para las enzimas tratadas es la línea negro y para las enzimas no tratadas es la línea roja.

5.3.2 Algunas consideraciones

Finalmente, algunas consideraciones que se debe de tener a la hora de estimar un modelo no lineal:

• Lo ideal es que el algoritmo llegue a la solución en pocas iteraciones.

• Siempre es bueno evaluar la solución con diferentes puntos iniciales. Es posible que caigamos en un máximo local.

• Si el tamaño de muestra no es grande, las propiedades asintóticas pueden no ser adecuadas. Por lo tanto, es mas conveniente usar bootstrap para hacer inferencias.