Capítulo 9 Modelo lineal mixto
9.1 Casos de estudio
9.1.1 Peso al nacer de ratas
Los datos ratpup de la librería WWGbook corresponden a un estudio donde se asignaron aleatoriamente 30 ratas hembra para recibir una de tres dosis (Alta, Baja o Control) de un compuesto experimental. El objetivo es determinar como este compuesto afecta el peso al nacer de las crías.
En la Figura 9.1 se puede observar que el peso de los machos tiende a ser un poco mayor que el de las hembras. En término de los tratamientos, las crías que pertenecen a las madres que recibieron las dosis del compuesto experimental tienen pesos levemente inferiores. Además, vemos que las medidas del peso de las crías que pertenecen a la misma camada son más parecidas entre ellas que las observaciones entre camadas. Esto puede ser un indicio de que las observaciones dentro de la misma camada estén correlacionadas, sin embargo, se podría asumir que las observaciones entre camadas sean independientes.
library(WWGbook)
data(ratpup)
plot(ratpup$litter,ratpup$weight,col=as.double(ratpup$sex),pch=19,xlab='camada', ylab='peso al nacer (gramos)')
abline(v=c(10.5,20.5),lty=2)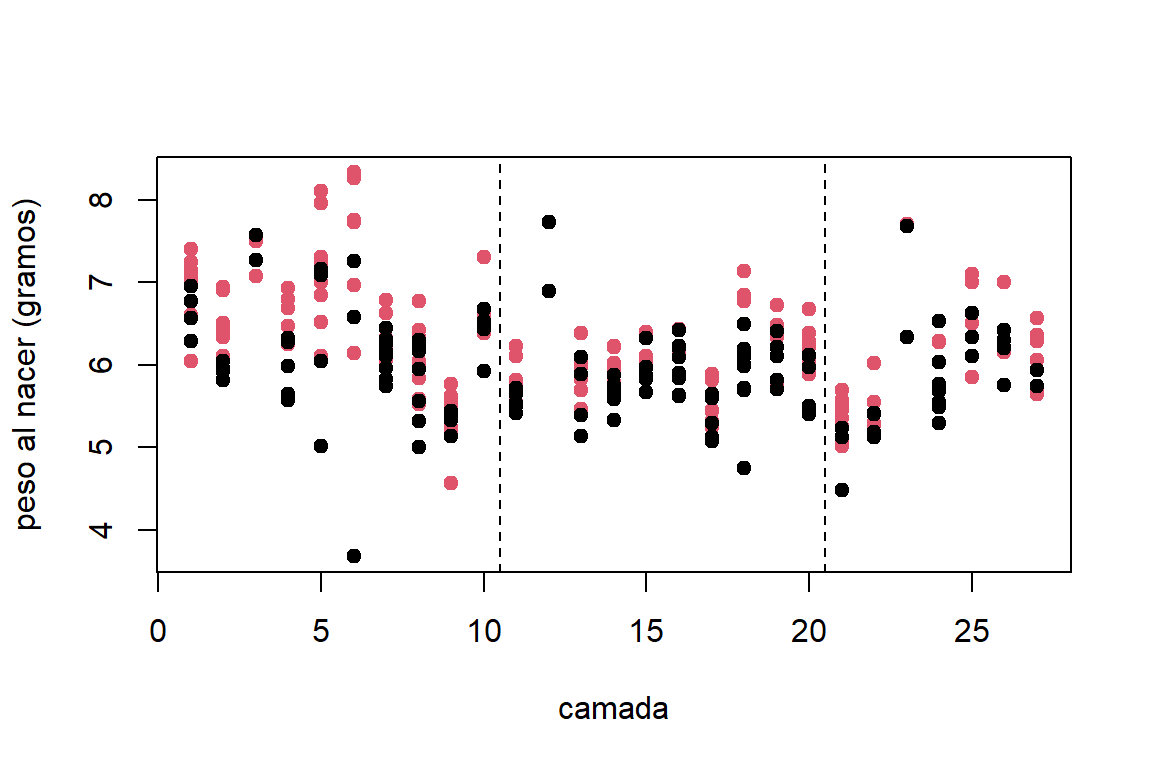
Figure 9.1: Datos del peso al nacer de ratas. Diagrama de dispersión de peso de la cría por camada. Los puntos negros corresponden a las hembras y los rojos a los machos. Las primeras diez camadas corresponden al control, las siguientes diez a la dosis baja y las últimas diez a la dosis alta.
9.1.2 Capacidad respiratoria
El volumen espiratorio forzado (FEV) es la cantidad de aire que una personal puede exhalar (en litros por segundo) durante una respiración forzada . Los datos fev.txt (Disponible aquí) pertenece a un estudio que tiene como objetivo determinar como dos medicamentos experimentales afecta la capacidad respiratoria de los pacientes, la cual se cree es un efecto secundario a corto plazo del tratamiento. Para esto, se asignó de forma aleatoria \(72\) pacientes hombres en tres grupos, droga A, droga B y control (placebo). A cada paciente, el FEV fue medido antes administrar los tratamientos (baseline) y luego cada hora durante 8 horas consecutivas.
La Figura 9.2 muestra las trayectorias individuales de cada individuo. Se puede observar una tendencia negativa del FEV en el tiempo para los pacientes que se encuentran en los tratamientos. Mientras que, para los pacientes del grupo placebo se observa que el FEV es constante en el tiempo. Además, se observa que hay poca variabilidad en las mediciones que pertenecen al mismo individuo. Por el contrario, hay mucha variabilidad entre individuos.
library(ggplot2)
fev = read.table('fev.txt',header = T)
fev$drug = as.factor(fev$drug)
levels(fev$drug) = c('A','B','Placebo')
p <- ggplot(data = fev, aes(x = hour, y = fev, group = patient))
p + geom_line() + facet_grid(. ~ drug) + ylab('Volumen espiratorio forzado (litros por segundo)') + xlab('tiempo (horas)')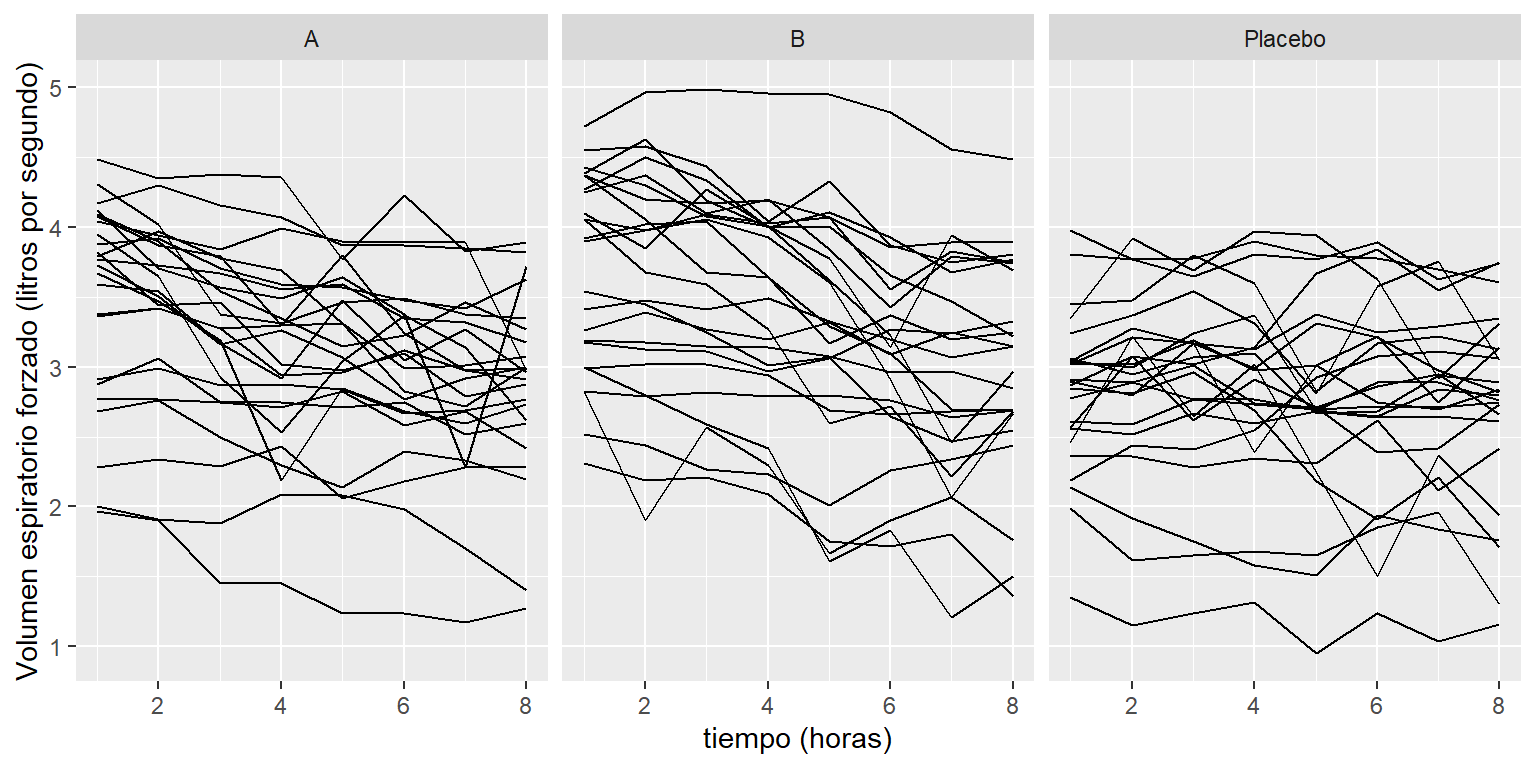
Figure 9.2: Datos de capacidad respiratoria. Mediciones del volumen espiratorio forzado por hora de los pacientes en cada uno de los grupos.
9.2 Datos por cluster (correlacionados)
En ambos estudios se tienen datos que pueden estar correlacionados. Este tipo de datos son llamados por cluster (jerárquicos o multinivel) dado que pueden ordenarse jerárquicamente. Por ejemplo:
En el estudio del peso de las ratas, se espera que las crías que pertenecen a la misma camada (madre) estén correlacionados. Por lo que el cluster está definido por la camada.
En el estudio sobre capacidad pulmonar, las mediciones que pertenecen al mismo individuo pueden estar correlacionadas. Por lo que el paciente define el cluster.
En un estudio sobre resultados de estudiantes de una muestra de escuelas se puede tener correlaciones entre estudiantes de la misma clase, o de estudiantes que pertenecen a la misma escuela. Por lo que se tienen tres niveles: escuelas - salones - estudiantes.
9.3 Notación
Para el cluster \(i\), se tienen \(n_i\) observaciones. Por lo que ahora tenemos un vector respuesta para el \(i\)-ésimo cluster: \(\boldsymbol y_i = (y_{i1},\ldots,y_{in_i})'\), para \(i=1,\ldots,N\). Sea \(\boldsymbol x_{ij}\) el vector \(p\)-dimensional de covariables asociadas a la observación \(y_{ij}\).
9.4 Modelos con intercepto aleatorios
Definimos a \(y_{ij}\) como el peso de la \(j\)-ésima cría de la camada \(i\). Por lo que, \(\boldsymbol y_i\) corresponde al vector de pesos de las crías de la madre \(i\). Para inducir correlación entre las observaciones (pesos de las crías) del mismo cluster (madre) se puede incluir un efecto aleatorio en el modelo lineal: \[ y_{ij} = \beta_0 + b_i + \mbox{sex}_{ij}\beta_1+ \mbox{treat1}_{i}\beta_2 + \mbox{treat2}_{i}\beta_3 + \varepsilon_{ij}, \] donde sex\(_{ij}=1\) si la \(j\)-ésima cría de la camada \(i\) es macho, sex\(_{ij}=1\) si lo contrario; treat1\(_{i}=1\) si la madre \(i\) recibió la dosis baja, treat1\(_{i}=0\) si lo contrario; treat2\(_{i}=1\) si la madre \(i\) recibió la dosis alta, treat2\(_{i}=0\) si lo contrario. Además, asumimos que \(b_i\) y \(\varepsilon_{ij}\) son independientes y \(b_i \sim N(0,d)\) y \(\varepsilon_{ij} \sim N(0,\sigma^2)\).
Por lo que condicionalmente a \(b_i\), se tiene que: \[ E(y_{ij} | b_i)= \beta_0 + b_i + \mbox{sex}_{ij}\beta_1+ \mbox{treat}_{1i}\beta_2 + \mbox{treat}_{2i}\beta_3 \mbox{ y } v(y_{ij} | b_i)= \sigma^{2}. \] Mientras que, marginalmente: \[ E(y_{ij}) = E\left[ E(y_{ij} | b_i) \right] = \beta_0 + \mbox{sex}_{ij}\beta_1+ \mbox{treat}_{1i}\beta_2 + \mbox{treat}_{2i}\beta_3, \] y \[ V(y_{ij}) = E\left[ V(y_{ij} | b_i) \right] + V\left[ E(y_{ij} | b_i) \right] = \sigma^{2} + d. \] Además, \[ cov(y_{ij},y_{ik}) = d \mbox{ y } cov(y_{i^{*}j},y_{ik}) = 0. \] Esto quiere decir que los pesos de las crías que pertenecen a la misma camada están correlacionadas, con \(cor(y_{ij},y_{ik}) = d/(\sigma^2+d)\). La matriz de covarianza y correlación de \(y_{ij}\) son: \[ \boldsymbol V_{i} = \begin{pmatrix} \sigma^{2} + d & d & d & \ldots & d \\ d & \sigma^{2} + d & d & \ldots & d \\ d & d & \sigma^{2} + d & \ldots & d \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ d & d & d & \ldots & \sigma^{2} + d \\ \end{pmatrix} \mbox{ y } \boldsymbol R_{i} = \begin{pmatrix} 1 & \frac{d}{\sigma^{2} + d} & \frac{d}{\sigma^{2} + d} & \ldots & \frac{d}{\sigma^{2} + d} \\ \frac{d}{\sigma^{2} + d} & 1 & \frac{d}{\sigma^{2} + d} & \ldots & \frac{d}{\sigma^{2} + d} \\ \frac{d}{\sigma^{2} + d} & \frac{d}{\sigma^{2} + d} & 1 & \ldots & \frac{d}{\sigma^{2} + d} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \frac{d}{\sigma^{2} + d} & \frac{d}{\sigma^{2} + d} & \frac{d}{\sigma^{2} + d} & \ldots & 1 \\ \end{pmatrix}. \] Mientras que se asume que hay incorrelación entre los pesos de crías de diferente camada.
9.4.1 Modelo con pendiente aleatoria
Sea \(y_{ij}\) la diferencia del FEV del \(j\)-ésimo paciente antes de iniciar el tratamiento y en la hora \(t_{j}\), para \(t_{j}= \{1,2,\ldots,8\}\). Por lo tanto, \(\boldsymbol y_i\) corresponde al vector de mediciones del FEV del paciente \(i\) a lo largo del tiempo.
En este caso el modelo de intercepto aleatorio no es conveniente, puesto que este asume que todas las correlaciones de las observaciones del mismo cluster son iguales. Con datos de longitudinales lo que se espera que la correlación dependa de la distancia en el tiempo en que se hayan tomado las observaciones. Por ejemplo, \(cor(y_{i1}, y_{i2}) > cor(y_{i1}, y_{i3}) > cor(y_{i1}, y_{i4})\). En este caso, se puede proponer un modelo con pendiente aleatoria: \[ y_{ij} = \beta_{0} + b_{0i} + \mbox{drugA}_{i}\beta_{2} + \mbox{drugB}_{i}\beta_{3} + t_j \beta_4 + t_jb_{1i} + \mbox{drugA}_{i}t_j\beta_{5} + \mbox{drugB}_{i}t_j\beta_{6} + \varepsilon_{ij}, \] donde drugA\(_{i}=1\) si el paciente \(i\) recibió la droga A, drugA\(_{i}=0\) si lo contrario; donde drugB\(_{i}=1\) si el paciente \(i\) recibió la droga B, drugB\(_{i}=0\) si lo contrario; \(\boldsymbol b_i = (b_{0i},b_{1i}) \sim N(\boldsymbol 0,\boldsymbol D)\) y \(\varepsilon_{ij} \sim N(0,\sigma^2)\). Además, asumimos que \(\boldsymbol b_i\) y \(\varepsilon_{ij}\) son independientes.
En este caso, se tiene que el valor esperado marginal es: \[ E(y_{ij}) = \beta_{0} + \mbox{drugA}_{i}\beta_{2} + \mbox{drugB}_{i}\beta_{3} + t_j \beta_4 + \mbox{drugA}_{i}t_j\beta_{5} + \mbox{drugB}_{i}t_j\beta_{6}. \] La varianza marginal es: \[ V(y_{ij}) = V(b_{0i} + t_{j}b_{1i} + \varepsilon_{ij}) = d_{11}t_{j}^2 + 2d_{01}t_{j} + d_{00} + \sigma^{2}. \] Finalmente, la covarianza es: \[ Cov(y_{ij},y_{ik}) = Cov(b_{0i} + t_{j}b_{1i} + \varepsilon_{ij},b_{0i} + t_{j}b_{1i} + \varepsilon_{ik}) = d_{11}t_{j}t_{k} + d_{01}(t_{j}+t_{k}) + d_{00}. \] Aquí vemos que al incluir una pendiente aleatoria, el modelo permite heterogeneidad de varianza y la correlación depende de los tiempos en que se tomaron las mediciones.
9.5 Modelo lineal mixto
De forma general, el modelo lineal mixto se puede expresar de la siguiente forma: \[ \boldsymbol y_{i} = \boldsymbol X_{i}\boldsymbol \beta+ \boldsymbol Z_{i}\boldsymbol b_{i} + \boldsymbol \varepsilon_i. \] donde \(\boldsymbol X_i\) y \(\boldsymbol Z_i\) son matrices de dimensión \(n \times p\) y \(n \times q\), \(\boldsymbol b_i\) es el vector \(q\)-dimensional de efectos aleatorios, y \(\boldsymbol \varepsilon_i\) es el vector \(n\)-dimensional de errores asociados al \(i\)-ésimo cluster. Además, se asume que: \[ \boldsymbol b_{i}\sim N(\boldsymbol 0,\boldsymbol D) \mbox{ y }\boldsymbol \varepsilon_{i} \sim N(\boldsymbol 0,\sigma^{2}\boldsymbol I), \] y que \(\boldsymbol b_{i}\) y \(\boldsymbol \varepsilon_{i}\) son independientes. Por lo tanto, marginalmente tenemos que: \[ E(\boldsymbol y_{i}) = \boldsymbol X_{i}\boldsymbol \beta\mbox{ y } V(\boldsymbol y_{i}) = \boldsymbol V_{i} = \boldsymbol Z_{i}\boldsymbol D\boldsymbol Z_{i}' + \sigma^{2}\boldsymbol I. \] Aquí estamos asumiendo independencia condicional. Esto es, \(V(\boldsymbol \varepsilon_{i}) = \sigma^{2}\boldsymbol I\). Sin embargo, se puede agregar una estructura a la componente de varianza del error, \(V(\boldsymbol \varepsilon_{i}) =\boldsymbol \Sigma_i\).
9.6 Estimación de los parámetros
La estimación de los parámetros se hace a través de máxima verosimilitud. Sea \(\boldsymbol \theta= (\boldsymbol \beta',\boldsymbol \alpha)'\), donde \(\boldsymbol \alpha\) son los parámetros asociados a \(\boldsymbol D\) y \(\boldsymbol \Sigma_i\). La función de log-verosimilitud está defina como: \[\begin{equation} \ell(\boldsymbol \theta) \propto \sum_{i=1}^{N} \left[ -\frac{1}{2}\log |\boldsymbol V_i(\boldsymbol \alpha)| - \frac{1}{2}(\boldsymbol y_{i} - \boldsymbol X_{i}\boldsymbol \beta)'\boldsymbol V_i(\boldsymbol \alpha)^{-1}(\boldsymbol y_{i} - \boldsymbol X_{i}\boldsymbol \beta) \right]. \tag{9.1} \end{equation}\] Se define \(\boldsymbol V_i=\boldsymbol V_i(\boldsymbol \alpha)\) para enfatizar que la matriz de varianza marginal depende de los parámetros contenidos en \(\boldsymbol \alpha\). No hay solución analítica para maximizar (9.1), por lo que la estimación se hace por métodos iterativos (algoritmos basados en Newton-Raphson).
Otra alternativa es a través de máxima verosimilitud restringida (REML). Este método proporciona estimaciones para \(\boldsymbol \alpha\) con menor sesgo. De todas formas, tanto las estimaciones por ML y REML son consistentes, eficientes y asintóticamente normales. Para ajustar un modelo lineal mixto en R podemos utilizar la función lme de la librería nlme.
9.6.1 Estimación del modelo con intercepto aleatorio
Para los datos del peso de las ratas, el ajuste del modelo por REML lo podemos hacer de la siguiente forma:
library(nlme)
mod.ratpup = lme(weight~sex+treatment, random=~1|litter,data=ratpup)
summary(mod.ratpup)## Linear mixed-effects model fit by REML
## Data: ratpup
## AIC BIC logLik
## 431.6577 454.23 -209.8288
##
## Random effects:
## Formula: ~1 | litter
## (Intercept) Residual
## StdDev: 0.5708847 0.4044791
##
## Fixed effects: weight ~ sex + treatment
## Value Std.Error DF t-value p-value
## (Intercept) 6.244974 0.18668230 294 33.45241 0.0000
## sexMale 0.361273 0.04779857 294 7.55823 0.0000
## treatmentHigh -0.354683 0.28930612 24 -1.22598 0.2321
## treatmentLow -0.374705 0.26172392 24 -1.43168 0.1651
## Correlation:
## (Intr) sexMal trtmnH
## sexMale -0.150
## treatmentHigh -0.633 0.017
## treatmentLow -0.701 0.026 0.450
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -7.46481761 -0.45010149 0.01750892 0.54197117 3.13826976
##
## Number of Observations: 322
## Number of Groups: 27A través del argumento random=~1|litter estamos indicando que hay un intercepto aleatorio asociado a la variable litter (camada). La varianza total del peso de las crías es \(0.164+0.326=0.49\). Mientras que, la correlación entre crías de la misma camada es:
\[
\rho_{I} = \frac{0.326}{0.326+0.164} = 0.665.
\]
Ahora, los resultado de los efectos fijos muestran que el peso de las crías machos tienen un peso significativamente mayor que el de las crías hembras. Evaluando los coeficientes asociados a los tratamiento, se observa que son negativos. Sin embargo, estos efectos parecen ser no significativos (se tiene que confirma con una prueba conjunta). Este último resultado es contrario al que se obtiene con el modelo lineal (sin asumir correlación entre las observaciones, usando la función lm).
Para evaluar si los tratamientos tienen un efecto significativo, se plantea el siguiente sistema de hipótesis: \[ H_0: \beta_2 = \beta_3 = 0. \] La prueba de hipótesis la podemos realizar a través de la prueba de razón de verosimilud de la siguiente forma:
mod.ratpup0 = lme(weight~sex, random=~1|litter,data=ratpup,method='ML')
mod.ratpup1 = lme(weight~sex+treatment, random=~1|litter,data=ratpup,method='ML')
anova(mod.ratpup0,mod.ratpup1)## Model df AIC BIC logLik Test L.Ratio p-value
## mod.ratpup0 1 4 421.6434 436.7416 -206.8217
## mod.ratpup1 2 6 422.9754 445.6227 -205.4877 1 vs 2 2.667947 0.2634Estos resultados confirmar que no hay un efecto de los tratamientos sobre el peso de las crías. Hay que tener en cuenta que para realizar una prueba de razón de verosimilitud sobre los efectos fijos (\(\boldsymbol \beta\)) es necesario estimar los parámetros por máxima verosimilitud.
9.6.2 Estimación del modelo con pendiente aleatoria
Ahora, podemos estimar el modelo de pendiente aleatoria para los datos de la capacidad respiratoria de la siguiente forma:
fev$fevdiff = fev$fev - fev$base
fev$drug=relevel(fev$drug,'Placebo')
lmm.fev = lme(fevdiff~hour*drug, random=~hour|patient,data=fev)
summary(lmm.fev)## Linear mixed-effects model fit by REML
## Data: fev
## AIC BIC logLik
## 237.5878 281.0442 -108.7939
##
## Random effects:
## Formula: ~hour | patient
## Structure: General positive-definite, Log-Cholesky parametrization
## StdDev Corr
## (Intercept) 0.51220391 (Intr)
## hour 0.06040257 -0.459
## Residual 0.20700812
##
## Fixed effects: fevdiff ~ hour * drug
## Value Std.Error DF t-value p-value
## (Intercept) 0.2592411 0.10961492 501 2.365016 0.0184
## hour -0.0184772 0.01394747 501 -1.324770 0.1859
## drugA 0.5999851 0.15501891 69 3.870400 0.0002
## drugB 0.9422619 0.15501891 69 6.078367 0.0000
## hour:drugA -0.0714782 0.01972470 501 -3.623791 0.0003
## hour:drugB -0.0968105 0.01972470 501 -4.908086 0.0000
## Correlation:
## (Intr) hour drugA drugB hr:drA
## hour -0.512
## drugA -0.707 0.362
## drugB -0.707 0.362 0.500
## hour:drugA 0.362 -0.707 -0.512 -0.256
## hour:drugB 0.362 -0.707 -0.256 -0.512 0.500
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -4.366026703 -0.428767946 0.009979273 0.517082034 3.142966988
##
## Number of Observations: 576
## Number of Groups: 72Estos resultados muestran que, para los pacientes del grupo control, el FEV no cambia con el tiempo. Esto es esperado dado que estos pacientes no recibieron ningún medicamento que pudiera modificar su capacidad espiratoria. Mientras que, los tratamientos tienen un efecto negativo significativo sobre la capacidad espiratoria. Esto se puede observar de forma gráfica en la Figura 9.3.
betaEst = lmm.fev$coefficients$fixed
mean.line = data.frame(a = c(betaEst[1],betaEst[1] + betaEst[3], betaEst[1] + betaEst[4]),
b= c(betaEst[2],betaEst[2] + betaEst[5], betaEst[2] + betaEst[5]),
drug = c('Placebo','A','B'))
p <- ggplot(data = fev, aes(x = hour, y = fevdiff, group = patient))
p + geom_line() + facet_grid(. ~ drug) + ylab('diferencia del FEV (litros por segundo)') + xlab('tiempo (horas)') + geom_abline(data=mean.line,aes(intercept = a, slope = b),col=2,lwd=2)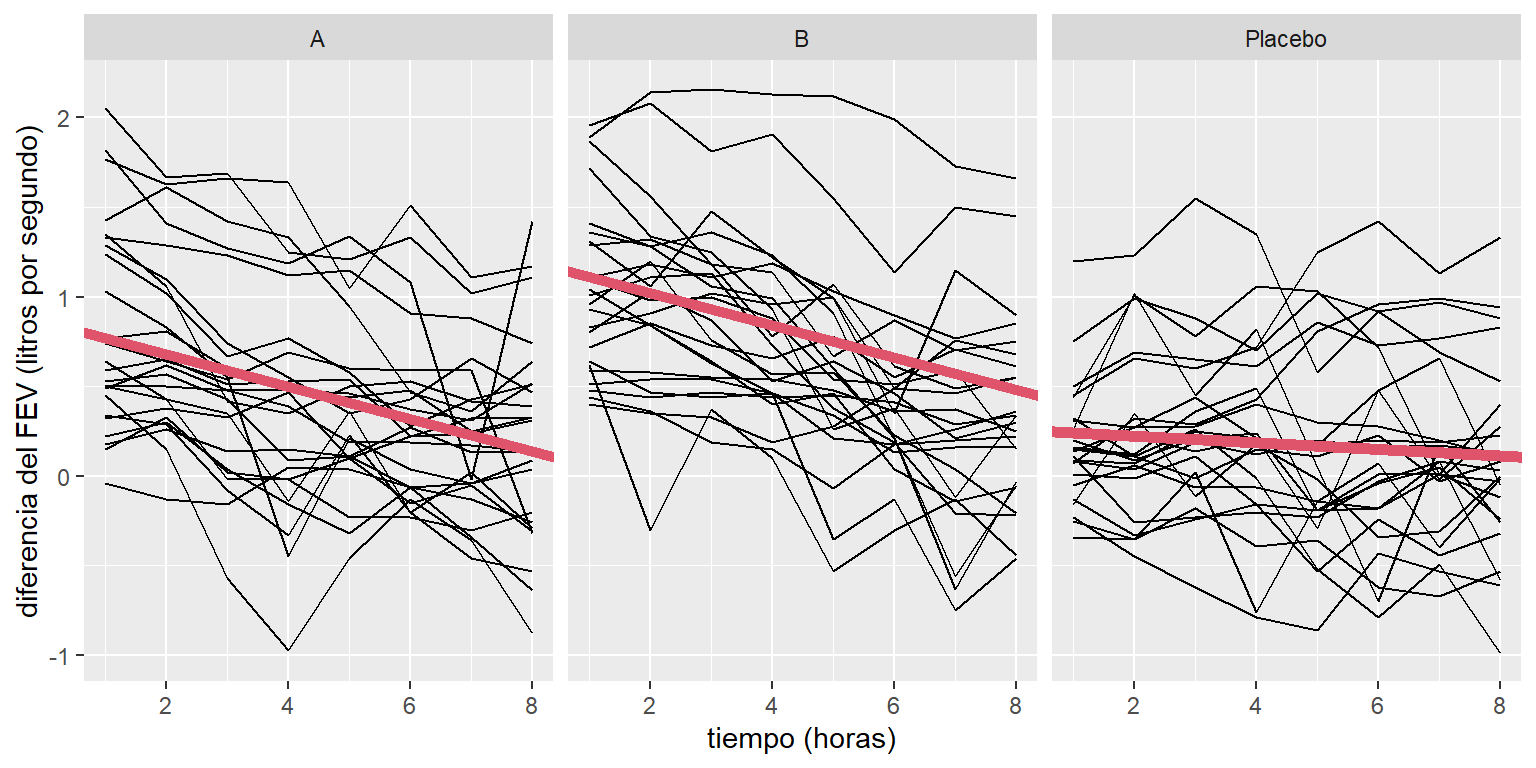
Figure 9.3: Datos de capacidad respiratoria. Estimación de la media de la diferencia del Volumen espiratorio forzado por hora (línea roja) para los pacientes en cada uno de los grupos.
La estimación de la varianza y correlacion marginal se puede obtener a través de la función getVarCov. Por ejemplo, la estimación de la matriz de varianza y correlación marginal para el individuo uno es:
## patient 1
## Marginal variance covariance matrix
## 1 2 3 4 5 6 7 8
## 1 0.28045 0.22705 0.21650 0.20595 0.19539 0.18484 0.17429 0.16374
## 2 0.22705 0.26300 0.21324 0.20634 0.19944 0.19253 0.18563 0.17873
## 3 0.21650 0.21324 0.25284 0.20673 0.20348 0.20022 0.19697 0.19372
## 4 0.20595 0.20634 0.20673 0.24998 0.20752 0.20792 0.20831 0.20870
## 5 0.19539 0.19944 0.20348 0.20752 0.25442 0.21561 0.21965 0.22369
## 6 0.18484 0.19253 0.20022 0.20792 0.21561 0.26615 0.23099 0.23868
## 7 0.17429 0.18563 0.19697 0.20831 0.21965 0.23099 0.28518 0.25367
## 8 0.16374 0.17873 0.19372 0.20870 0.22369 0.23868 0.25367 0.31151
## Standard Deviations: 0.52958 0.51283 0.50283 0.49998 0.5044 0.5159 0.53402 0.55813## 1 2 3 4 5 6 7
## 1 1.0000000 0.8360136 0.8130169 0.7778053 0.7314927 0.6765661 0.6162925
## 2 0.8360136 1.0000000 0.8269414 0.8047373 0.7710037 0.7277256 0.6778195
## 3 0.8130169 0.8269414 1.0000000 0.8223095 0.8022765 0.7718468 0.7335290
## 4 0.7778053 0.8047373 0.8223095 1.0000000 0.8228830 0.8060672 0.7801834
## 5 0.7314927 0.7710037 0.8022765 0.8228830 1.0000000 0.8285640 0.8154488
## 6 0.6765661 0.7277256 0.7718468 0.8060672 0.8285640 1.0000000 0.8384306
## 7 0.6162925 0.6778195 0.7335290 0.7801834 0.8154488 0.8384306 1.0000000
## 8 0.5539758 0.6244266 0.6902507 0.7478984 0.7945883 0.8289286 0.8510795
## 8
## 1 0.5539758
## 2 0.6244266
## 3 0.6902507
## 4 0.7478984
## 5 0.7945883
## 6 0.8289286
## 7 0.8510795
## 8 1.0000000Aquí vemos que la varianza de la diferencia del FEV no tiene un cambio notable en tiempo. Con respecto a las correlaciones, estas son mayores cuando las observaciones están más cercanas en el tiempo. Este último resultado es común con datos de tipo longitudinal.