Capítulo 6 Modelo lineal generalizado
6.1 Introducción
Asumiendo independencia entre las observaciones \(y_1,\ldots,y_n\), los modelos lineales se expresan como: \[ \boldsymbol y=\boldsymbol X\boldsymbol \beta+\boldsymbol \varepsilon, \quad \text{donde}\quad \boldsymbol \varepsilon\sim N(\boldsymbol 0,\sigma^2\boldsymbol I), \] donde \(\boldsymbol y\) es el vector de variable respuesta, \(\boldsymbol X\) es la matriz \(n \times p\) de covariables, \(\boldsymbol \beta\) el vector de coeficientes, y \(\boldsymbol \varepsilon\) el vector de los errores. De aquí podemos derivar que \(\boldsymbol y\sim N(\boldsymbol X\boldsymbol \beta, \sigma^{2}\boldsymbol I)\). Esto implica, entre otras cosas, que:
- hay una relación lineal entre el valor esperado de la variable respuesta y el conjunto de covariables,
- la varianza de la variable respuesta es constante,
- la inferencia asume que la variable respuesta sigue una distribución normal.
Sin embargo, hay situaciones en donde estas propiedades no son factibles, incluso luego de hacer transformaciones sobre las variables. Por ejemplo, si la variable de respuesta es dicotómica \((y_{i}\in\{0,1\})\) no podríamos representar \(E(y|\boldsymbol x)\) como una función lineal. Además, la distribución asociada dificilmente serían normal. Aquí es mas conveniente es proponer una distribución de probabilidad diferente, por ejemplo, una Bernoulli, y ajustar un modelo lineal generalizado (GLM).
6.2 Casos de estudio
6.2.1 Mortalidad de escarabajos
En un estudio de toxicología, se está interesado en la tasa de mortalidad de escarabajos expuestos a disulfuro de carbono gaseoso. La Tabla 6.1 muestra el número de escarabajos muertos después de cinco horas de exposición de este tóxico a diferentes concentraciones del químico. Podemos ver que a medida que aumenta la dosis, la mortalidad de escarabajos va aumentando.
| log. dosis | expuestos | muertos |
|---|---|---|
| 1.6907 | 59 | 6 |
| 1.7242 | 60 | 13 |
| 1.7552 | 62 | 18 |
| 1.7842 | 56 | 28 |
| 1.8113 | 63 | 52 |
| 1.8369 | 59 | 53 |
| 1.8610 | 62 | 61 |
| 1.8839 | 60 | 60 |
Lectura de datos en R:
En la Figura 6.1 podemos observar como es el aumento de la tasa de mortalidad con respecto a la dosis del tóxico. Note que la relación no es lineal, si no que tiene una forma de ‘S’. Esto hace que un modelo de regresión lineal sea inadecuado (además una línea recta permitiría estimaciones por debajo de cero y encima de 1).
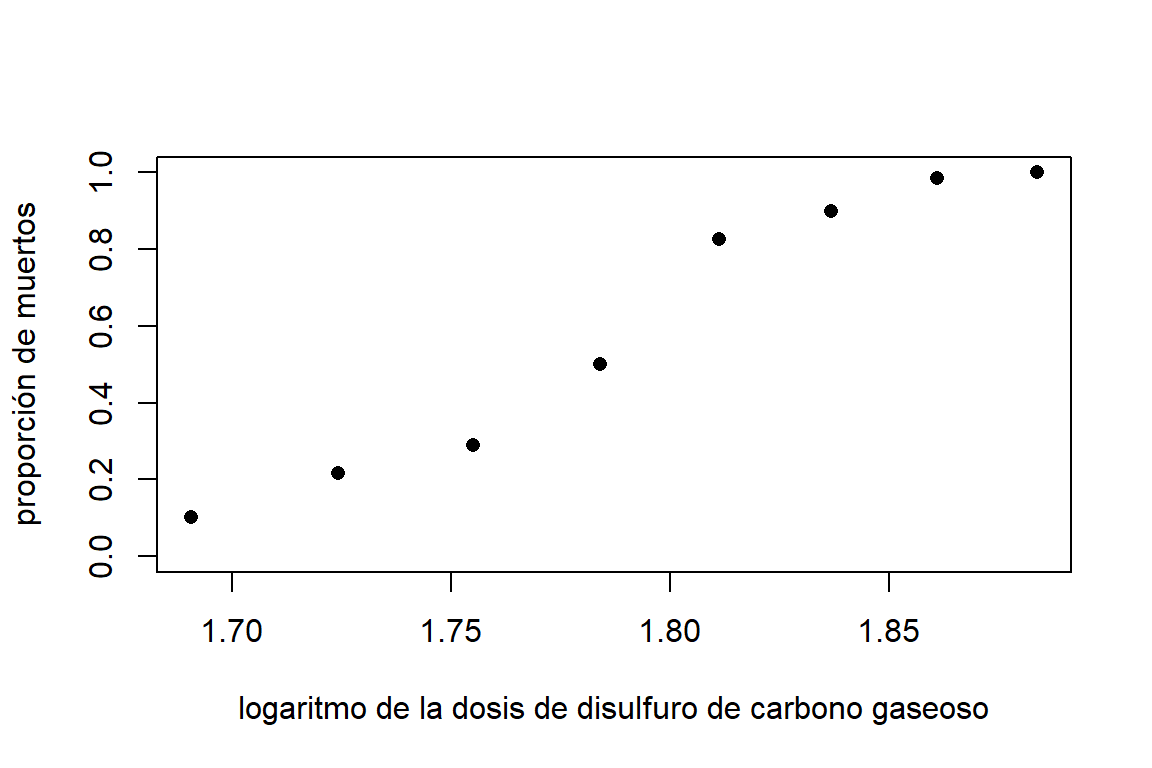
Figure 6.1: Datos de mortalidad de escarabajos. Relación entre la concentración de disulfuro de carbono gaseoso (en escala logarítmica) y la proporción de muertes (muertos/expuestos) de los escarabajos.
Una alternativa es utilizar una transformación que describa la relación de forma adecuada y que garantice que la respuesta se encuentre dentro del espacio del parámetro. Es decir, que la estimación de la proporción de escarabajos muertos esté entre \(0\) y \(1\).
6.2.2 ataques de epilepsia
Los datos data(epilepsy) de la librería HSAUR2 corresponden a un ensayo clínico para evaluar el efecto del fármaco Progabida sobre los ataques epilépticos. Al inicio del estudio, los \(59\) pacientes epilépticos fueron observados durante 8 semanas, y se registró el número de convulsiones. Luego, fueron aleatorizados al tratamiento con el fármaco Progabide (\(31\) pacientes) o al grupo de placebo (\(28\) pacientes). A los pacientes de ambos grupos se les observo durante cuatro períodos de dos semanas y se registró el número de convulsiones.
Estos datos son de naturaleza longitudinal (cada paciente cuenta con 4 observaciones tomadas en el tiempo), lo que requiere metodologías que tengan en cuenta la correlación que hay en los datos. En es caso, no consideraremos las observaciones intermedias de cada paciente, sino solamente las mediciones tomadas luego de las cuatro semanas de observación.
Las variables que se tendrán en cuenta son las siguientes:
* age: edad del paciente,
base: número de ataques epilépticos en las 8 semanas antes de iniciar los tratamientos,treatment: tratamiento (placebo, Progabida),seizure.rate(variable respuesta): número de ataques epilépticos en las últimas dos semanas al final de estudio (luego cuatro semanas de tratamiento).
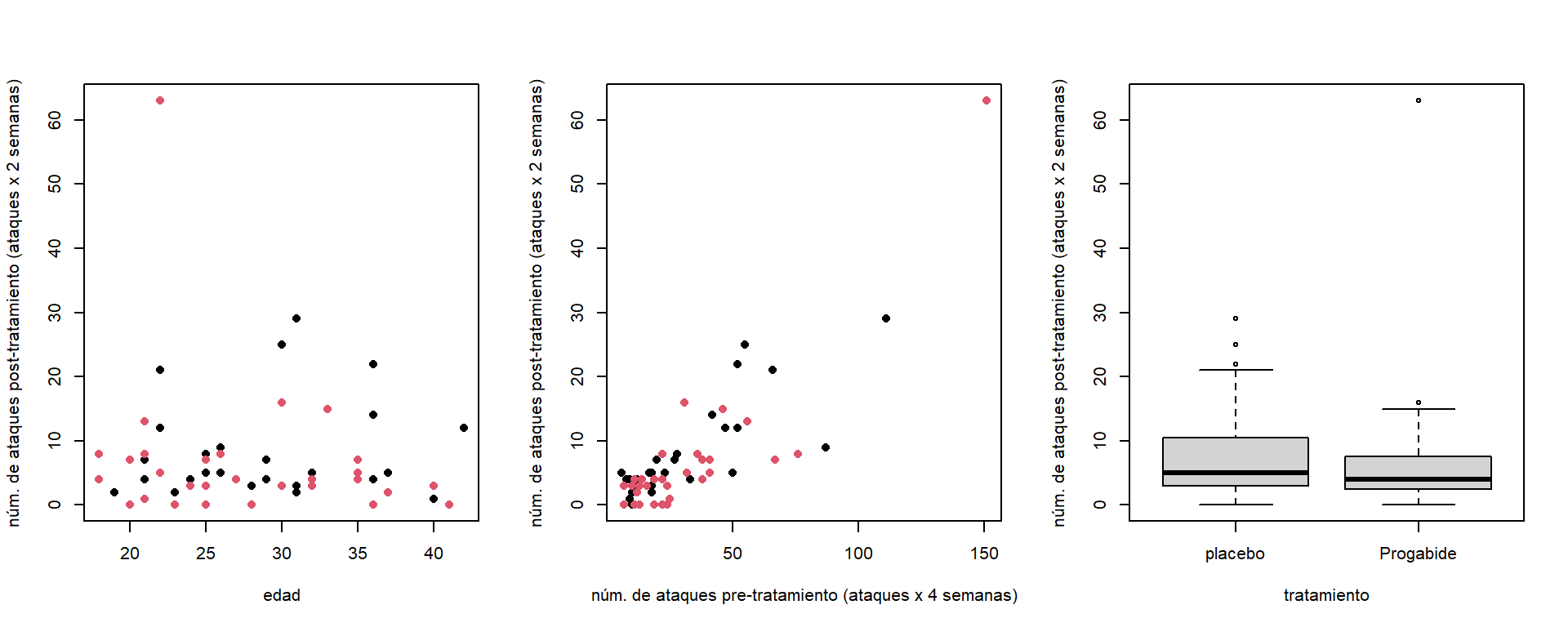
Figure 6.2: Datos de epilepsia. Relación entre el número de ataques epilépticos con la edad, ataques previos (izquierda) y el tratamiento (derecha).
La Figura 6.2 muestra la relación del número de ataques epiléticos al final del estudio con las posibles covariables. Aquí vemos que no parece haber relación con la edad, hay una relación positiva fuerte con el número de ataques pre-tratamiento, y que los pacientes del grupo placebo parecen presentar un poco más de convulsiones luego de las 8 semanas de tratamiento.
6.3 Preambulo
Antes de introducir los GLM, vamos a recordar algunos conceptos sobre distribuciones de probabilidad.
6.3.1 Familia exponencial
La distribución de probabilidad de una variable aleatoria \(Y\) pertenece a la familia exponencial si la función de densidad (o masa) de \(Y\) se puede expresar de la siguiente forma: \[ f(y;\theta,\phi)=\exp\{[y\theta-b(\theta)]/a(\phi)+c(y,\phi)\}, \]
donde \(\theta\) es llamado parámetro natural, y \(\phi>0\) es un parámetro de dispersión. Además se tiene que:
\[ E[Y]=b'(\theta) \quad \text{y} \quad V[Y]=b''(\theta)a(\phi). \] Por ejemplo, la distribución Poisson pertenece a la familia exponencial. Para demostrarlo, la función de densidad de la distribución Poisson:
\[ f(y;\mu)=\frac{\lambda^y\exp(-\lambda)}{y!}, \]
se puede reescribir como:
\[ f(y;\lambda)=\exp(-\lambda+y\log\lambda-\log y!). \] Por lo tanto, la distribución Poisson pertenece a la familia exponencial con \(\theta=\log\mu\), \(b(\theta)=\exp(\theta)\), \(a(\phi)=1\) y \(c(y,\phi)=-\log y!\).
La distribución normal también pertenece la familia exponencial. Su función de densidad,
\[ f(y;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma}}\exp\left[-\frac{(y-\mu )^2}{2\sigma^2}\right], \]
se puede reescribir como:
\[ f(y;\mu,\sigma^2)=\exp\left[\frac{y\mu-\frac{1}{2}\mu^2}{\sigma^2}-\frac{1}{2}\log(2\pi\sigma^2)-\frac{y^2}{2\sigma^2}\right], \]
donde \(\theta=\mu\), \(b(\theta)=\frac{1}{2}\theta^2\), \(a(\phi)=\sigma^2\) y \(c(y,\phi)=-\frac{1}{2}log(2\pi\sigma^2)-\frac{y^2}{2\sigma^2}\).
Finalmente, también la distribución binomial pertenece a la familia exponencial. Su función densidad,
\[ f(y;\pi)=\left(\begin{array}{c}n\\y\end{array}\right)\pi^y(1-\pi)^{n-y}. \] se puede reescribir como:
\[ f(y;\pi)=\exp\left\{y[\log\pi-\log(1-\pi)]+n\log(1-\pi)+\log\left(\begin{array}{c}n\\y\end{array}\right)\right\}, \] donde \(\theta=log\left(\frac{\pi}{1-\pi}\right)\), \(b(\theta)=-n\log\left[1+\exp(\theta)\right]\), \(c(\phi)=1\) y \(d(y,\phi)=\log\left(\begin{array}{c}n\\y\end{array}\right)\).
6.3.2 Relación media-varianza:
Para algunas distribuciones de probabilidad hay una relación directa entre la media y la varianza. Por ejemplo, para la distribución binomial tenemos que: \[ E(Y) = \mu = n\pi \mbox{ y } V(Y) = n\pi(1-\pi), \] por lo que \(V(Y) = \nu(\mu) = \mu(1-\mu)/n\).
Para la distribución Poisson, tenemos que \(V(Y) = \nu(\mu) = \mu\). Es decir, la varianza es igual a la media. Mientras que, para la distribución normal, la media y la varianza son parámetros independientes.
6.3.3 Estimador de máxima verosimilitud
Se asume que \(Y \sim f(y,\boldsymbol \theta)\) y estamos interesados en estimar \(\boldsymbol \theta\). Para ello tomamos una muestra independiente \((y_{1},y_{2},...,y_{n})\). Por lo que, la función de verosimilitud está definida como: \[ L(\boldsymbol \theta)=\prod_{i=1}^nf(y_{i};\boldsymbol \theta), \]
y la función de log-verosimilitud es: \[ \ell(\boldsymbol \theta)=\sum_{i=1}^n\log f(y_{i},\boldsymbol \theta). \]
El objetivo del estimador por máxima verosimilitud (MLE) es encontrar el \(\widehat{\boldsymbol \theta}\) que maximiza \(L(\boldsymbol \theta)\) (o \(\ell(\boldsymbol \theta)\)). Para esto, tenemos que calcular las derivadas de \(\ell(\boldsymbol \theta)\) con respecto a cada elemento de \(\boldsymbol \theta\) y resolver las ecuaciones score:
\[ \boldsymbol u(\boldsymbol \theta)=\frac{\partial\ell(\boldsymbol \theta)}{\partial\boldsymbol \theta}=\boldsymbol 0, \] para \(\boldsymbol \theta\). Es necesario verificar si la solución corresponde a un máximo de \(\ell(\boldsymbol \theta)\), evaluando si la matriz de segundas derivadas (matriz hessiana):
\[ \boldsymbol H(\boldsymbol \theta)=\frac{\partial^2\ell(\boldsymbol \theta)}{\partial\boldsymbol \theta\partial\boldsymbol \theta^{'}}, \] evaluada en \(\boldsymbol \theta=\widehat{\boldsymbol \theta}\), es negativa-definida.
6.3.3.1 Propiedades asintóticas de los MLEs
Las propiedades de los MLEs están basadas en teoría asintótica. Es decir, se cumplen cuando el tamaño de muestra es grande \((n\to \infty)\). \(\widehat{\boldsymbol \theta}\) es asintóticamente insesgado. Esto es, \(E(\widehat{\boldsymbol \theta})=\boldsymbol \theta\) cuando \(n\to \infty\). La varianza asintótica de \(\widehat{\boldsymbol \theta}\) se calcula como la inversa de la matriz de información: \[ V(\widehat{\boldsymbol \theta})=I(\boldsymbol \theta)^{-1},\quad \text{donde} \quad I(\boldsymbol \theta)=-E[H(\boldsymbol \theta)]. \] Por lo cual, es MLE es un estimador eficiente.
Además, \(\widehat{\boldsymbol \theta}\) es asintoticamente normal. Esto es, \(\widehat{\boldsymbol \theta}\sim N[\boldsymbol \theta,I(\boldsymbol \theta)^{-1}]\). Finalmente, el MLE cumple con la propiedad de invarianza. Si \(\widehat{\boldsymbol \theta}\) es el MLE de \(\boldsymbol \theta\), entonces \(g(\widehat{\boldsymbol \theta})\) es el MLE de \(g(\boldsymbol \theta)\).
6.3.4 Métodos iterativos de maximización
En algunos casos no es posible encontrar los MLEs de forma analítica, por lo que debemos hacerlo de forma iterativa. Los métodos que vamos a utilizar están basados en expansiones de series de Taylor.
Considere una expansión de series de Taylor de orden 1 para la función score, alrededor de \(\boldsymbol \theta=\boldsymbol \theta^{(t)}\):
\[ \boldsymbol u\left(\boldsymbol \theta\right)\approx \boldsymbol u\left(\boldsymbol \theta^{(t)}\right)+\boldsymbol H\left(\boldsymbol \theta^{(t)}\right)\left(\boldsymbol \theta-\boldsymbol \theta^{(t)}\right). \] Igualando la expresión anterior a cero tenemos que:
\[ \boldsymbol u\left(\boldsymbol \theta^{(t)}\right)+\boldsymbol H\left(\boldsymbol \theta^{(t)}\right)\left(\boldsymbol \theta-\boldsymbol \theta^{(t)}\right)=\boldsymbol 0, \] Ahora, encontramos la solución para \(\boldsymbol \theta^{(t+1)}\) de la siguiente forma: \[ \boldsymbol \theta^{(t+1)}=\boldsymbol \theta^{t}-\boldsymbol H\left(\boldsymbol \theta^{t}\right)^{-1}\boldsymbol u\left(\boldsymbol \theta^{t}\right). \] Podemos encontrar la estimación de \(\boldsymbol \theta\) repitiendo los pasos anteriores hasta que se cumpla un criterio de convergencia. Si reemplazamos \(\boldsymbol H(\boldsymbol \theta)\) por \(\boldsymbol I(\boldsymbol \theta)\), el algoritmo recibe el nombre de Fisher’s scoring.
6.4 Modelo lineal generalizado (GLM)
Un GLM está definido por tres componentes:
Componente aleatorio: variable respuesta \(Y\) y su distribución de probabilidad.
Predictor lineal: \(\eta=\boldsymbol x^{'}\boldsymbol \beta\), donde \(\boldsymbol \beta\) es un vector de parámetros y \(\boldsymbol x\) un vector de covariables.
Función de enlace: una función \(g\) que conecta la media de la variable respuesta, \(E(Y)\), con el predictor lineal, \(\eta\), \(g[E(Y|\boldsymbol x)]=\boldsymbol x'\boldsymbol \beta\).
6.4.1 Componente aleatorio
Se asume que se cuenta con \(n\) observaciones independientes \((y_{i},...,y_{n})\) de una variable aleatoria \(Y\) cuya distribución de probabilidad pertenece a la familia exponencial. Restringir un GLM a esta familia permite tener expresiones generales para la función de verosimilitud y funciones score, la distribución asintótica de los estimadores de los parámetros del modelo, y el algoritmo para ajustar el modelo.
Por ejemplo, para los datos de los escarabajos podemos asumir que el número de escarabajos que mueren, para cada dosis del químico, sigue una distribución binomial. Mientras que en el caso del ensayo clínico en epilepsia, se podría asumir que el número de ataques epilépticos, condicionado a las covariables, sigue una distribución Poisson.
6.4.2 Predictor lineal
Para cada observación \(i\), tenemos un conjunto de covariables observadas,
\[ \boldsymbol x_{i}=(1,x_{i1},...,x_{i,p-1})^{'}, \]
donde \(x_{ij}\) es la \(j\)-ésima covariable asociada al individuo \(i\). Entonces, el predictor lineal está definido como: \[ \eta_{i}=\beta_{0}+\sum_{j=1}^{p-1}\beta_{j}x_{ij}=\boldsymbol x_{i}^{'}\boldsymbol \beta. \]
6.4.3 Función de enlace
En algunas distribuciones,\(E(Y|\boldsymbol x)\) está acotada en un intervalo. Por ejemplo, en la distribución binomial, \(0\leq \pi_{i}\leq 1\), o en la Poisson, \(\lambda_{i}>0\). Esto hace que no siempre sea razonable asumir una relación lineal entre \(E(Y | \boldsymbol x)\) y \(\boldsymbol x\). Por lo que la función de enlace conecta \(E(Y|\boldsymbol x)\) con el predictor lineal \(\eta\) a través de una función \(g()\):
\[ E(Y|\boldsymbol x)=g^{-1}(\eta)=g^{-1}(\boldsymbol x^{'}\boldsymbol \beta), \] donde, la función \(g(\cdot)\) es monótona y diferenciable. Generalmente, \(g(\cdot)\) está determinada por la distribución que se asume para \(Y\).
6.4.4 Ejemplos de GLM
6.4.4.1 modelo logístico para la mortalidad de escarabajos
Sea: \[ y_{ij} = \begin{cases} 1 & \mbox{ si el escarabajo }j \mbox{ expuesto a la dosis }i\mbox{ muere,} \\ 0 & \mbox{ si lo contrario.} \end{cases} \] Por lo que, para \(i\)-ésima dosis, el número de escarabajos que muere es igual a \(y^*_i=\sum_{j=1}^{n_i} y_{ij}\). Además, asumiendo independencia, podemos decir que: \[ y^*_i \sim \mbox{binomial} (n_{i},\pi_{i}), i=1,\ldots,n_i, \] donde \(0 < \pi_i < 1\) depende de la dosis. Definiendo \(y_{i}=y^*_i/n_{i}\) (la proporción de escarabajos muertos para la dosis \(i\)), tenemos que: \[ E(y_{i}| \mbox{dosis}_{i}) = \pi_{i} \mbox{ y }V(y_{i}| \mbox{dosis}_{i}) = \pi_{i}(1-\pi_{i})/n_{i}. \]
Dado que \(0 \leq \pi_i \leq 1\), se podría proponer que: \[ \pi_{i} = g^{-1}(\mbox{dosis},\boldsymbol \beta) = \frac{\exp(\beta_0 + \log \ \mbox{dosis}_i\beta_1)}{1+\exp(\beta_0 + \log \ \mbox{dosis}_i\beta_1)} =\frac{\exp(\eta_i)}{1+\exp(\eta_i)}. \] Por lo que \(g(\pi_{i}) = \log \left( \frac{\pi_{i}}{1-\pi_{i}}\right) = \eta_i\). Esta función recibe el nombre de función logit y su forma la podemos ver gráficamente en la Figura 6.3. Como vemos, está función está acotada entre \(0\) y \(1\), garantizando que las probabilidades estimadas siempre estén en este rango, y tiene forma de ‘S’.
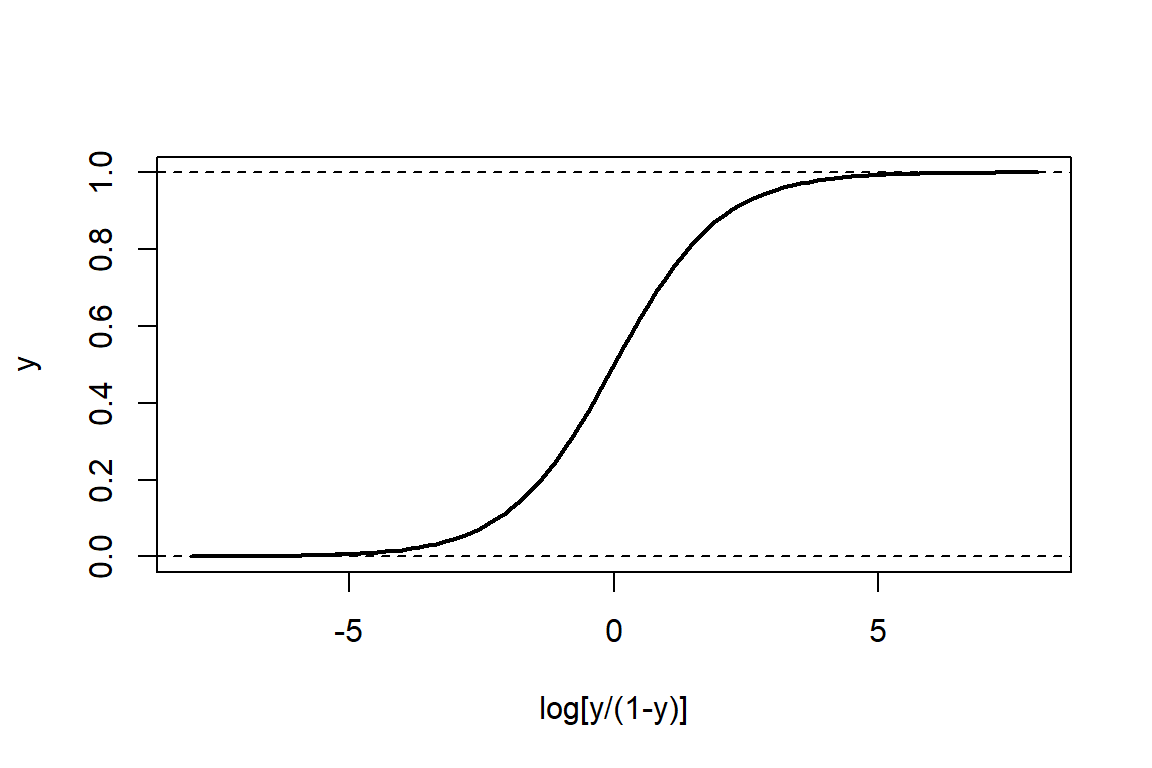
Figure 6.3: Función logística
6.4.4.2 modelo Poisson para el número de ataque epilépticos
Definiendo \(y_i\) como el número de ataques epilépticos (\(\times\) dos semanas) del paciente \(i\) luego de 8 semanas de tratamiento, podemos suponer que: \[ y_{i}\sim \mbox{Poisson}(\lambda_{i}), \quad i=1,...,n,\quad \text{donde} \quad \lambda_{i}=g(\eta_i), \] donde \(\eta_i = \beta_{0}+\beta_{1}\text{treat}_{i}+\beta_{2}\text{base}_{i}+\beta_{3}\text{base}_{i}\text{treat}_{i}.\) Entonces, \(E(y_{i}|\boldsymbol x_{i})=V(y_{i}|\boldsymbol x_{i})=\lambda_{i}\). Dado que \(\lambda_ i > 0\), se puede asumir que: \[ \lambda_{i}=g^{-1}(\eta_i)=\exp(\eta_i). \]
Por lo que, \(g(\lambda_{i})=\log\lambda_{i}\). Este modelo puede ser una opción para estimar el número medio de ataques epiléticos de los pacientes del ensayo clínico en epilepsia.
6.4.4.3 Otros ejemplos
Un modelo lineal es un caso particular del GLM. Aquí asumimos que \(y_i \sim N(\mu_i, \sigma^2)\), con \(\mu_i = \boldsymbol x_i'\boldsymbol \beta\). Esto es, la función de enlace es la identidad.
Otros ejemplos de distribuciones que se pueden utilizar son:
- Modelo binomial-negativo para conteo con sobredispersión.
- Modelo beta-binomial para ensayos Bernoulli correlacionados (sobredispersión).
- Modelo multinomial para variables nominales (ordinales) con más de dos categorías.
- Modelo beta para proporciones.
- Modelo gamma para variables continuas asimétricas y con varianza creciente.
- Modelo Weibull para tiempos de falla.
6.5 Ajuste de un GLM
Al igual que en los modelos lineales, los pasos para ajustar un GLM incluyen:
Especificación del modelo.Definición del componente aleatorio, predictor lineal y función de enlace.
Estimación de los parámetros. Para los GLM, la estimación se hace por máxima verosimilitud.
Evaluación del modelo. Verificar si el modelo estimado se ajusta bien a los datos.
Inferencia. cálculo de intervalos de confianza, pruebas de hipótesis e interpretación de los resultados según los objetivos del estudio.
6.5.1 Especificación del modelo
El GLM asume que:
\[ f(y_{i};\theta_{i},\phi)=exp\left\{\frac{y_{i}\theta_{i}-b(\theta_{i})}{a(\phi)} +c(y_{i},\phi)\right\}, \] donde \(\phi>0\). Además, \(E(y_{i})=b'(\theta_{i})\) y \(V(y_{i})=b''(\theta_{i})a(\phi).\)
El predictor lineal \(\eta_{i}=\boldsymbol x'_{i}\boldsymbol \beta\) se relaciona con \(\mu_{i}\) a través la función de enlace, \(\eta_{i}=g(\mu_{i})\).
La función de enlace \(g(\cdot)\) que transforma \(\mu_{i}\) en el parámetro natural \(\theta_{i}\) es llamada función de enlace canónica. Por ejemplo para la distribución normal, \(\eta_{i}=\mu_{i}\) (identidad), por lo tanto \(\mu_{i}=\eta_{i}\). Para la distribución Poisson, \(\eta_{i}=\log\mu_{i}\), por lo tanto \(\mu_{i}=\exp(\eta_{i})\). Para la distribución binomial, \(\eta_{i}=\log\left(\frac{\pi_{i}}{1-\pi_{i}}\right)\), por lo tanto \(\pi_{i}=\frac{\exp(\eta_{i})}{1+\exp(\eta_{i})}\).
6.5.2 Estimador por máxima verosimilitud para \(\boldsymbol \beta\)
dado que asumimos que la distribución de probabilidad asociada a la variable resputa pertenece a la familia exponencial, la función de log-verosimilitud está definida como: \[ \ell(\boldsymbol \beta)=\sum_{i=1}^{n}\ell_{i}(\boldsymbol \beta)=\sum_{i=1}^{n}\log f(y_{i};\theta_{i},\phi)=\sum_{i=1}^{n}\left[\frac{y_{i}\theta_{i}-b(\theta_{i})}{a(\phi)}+c(y_{i},\phi)\right]. \]
Las funciones score están definidas como:
\[ u(\beta_{j})=\sum_{i=1}^{n}\frac{(y_{i}-\mu_{i})x_{ij}}{V(y_{i})}\frac{\partial\mu_{i}}{\partial\eta_{i}}=0, \quad \text{para} \quad j=0,...,p-1, \] donde \(\eta_{i}=\boldsymbol x_{i}'\boldsymbol \beta=g(\mu_{i})\). Dado que las funciones score son no-lineales, es necesario estimar \(\boldsymbol \beta\) iterativamente usando el algoritmo de Newton-Raphson.
En forma matricial, tenemos que la función score es: \[ \boldsymbol u(\boldsymbol \beta)=\boldsymbol X'\boldsymbol D\boldsymbol V^{-1}(\boldsymbol y-\boldsymbol \mu), \] la función hessiana es: \[ \boldsymbol H(\boldsymbol \beta)=\boldsymbol I(\boldsymbol \beta)=\boldsymbol X'\boldsymbol W\boldsymbol X, \] donde \(\boldsymbol V\) es una matriz diagonal con valores \(v_{ii}=V(y_{i})\) en la diagonal, \(\boldsymbol D\) es una matriz diagonal con valores \(d_{ii}=\frac{\partial\mu_{i}}{\partial\eta_{i}}\),y \(\boldsymbol W\) es una matriz diagonal con \(w_{ii}=\frac{(\partial\mu_{i}/\partial\eta_{i})^2}{V(y_{i})}\).
A través del algoritmo de Newton-Raphson (o Fisher’s scoring) podemos encontrar la estimación de \(\boldsymbol \beta\) de forma iterativa: \[ \boldsymbol \beta^{(t+1)}=\boldsymbol \beta^{(t)}+[\boldsymbol I(\boldsymbol \beta^{(t)})]^{-1}\boldsymbol u(\boldsymbol \beta^{(t)}). \] Equivalentemente, podemos utilizar el método de mínimos cuadrados iterativamente reponderados:
\[ \boldsymbol \beta^{(t+1)}=(\boldsymbol X'\boldsymbol W^{(t)}\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol W^{(t)}\boldsymbol z^{(t)}, \] donde, los elementos de \(\boldsymbol z^{(t)}\) son:
\[ z_{i}^{(t)}=\boldsymbol x_{i}'\boldsymbol \beta^{(t)}+(y_{i}-\mu_{i}^{(t)})\frac{\partial\eta_{i}^{(t)}}{\partial \mu_{i}^{(t)}}. \]
La distribución asintótica del MLE de \(\boldsymbol \beta\) es:
\[ \widehat{\boldsymbol \beta}\sim N\left[\boldsymbol \beta,(\boldsymbol X'\boldsymbol W\boldsymbol X)^{-1}\right]. \] #### ajuste e interpretación de parámetros del modelo logístico
Para los datos de mortalidad de escarabajos, tenemos el siguiente modelo:
\[
y_i^* \sim \mbox{binomial}(n_i,\pi_i), \mbox{ donde } \pi_{i}=\frac{\exp(\beta_0+\beta_1\log\ \text{dosis}_i)}{1+\exp(\beta_0+\beta_0\log\ \text{dosis}_i)}.
\]
La estimación de los parámetros del GLM por MLE se puede hacer utilizando la función glm(). En esta función debemos determinar la distribución de probabilidad asociada a los datos y la función de enlace con el argumento family. Para el modelo logístico, usamos family=binomial (por defecto la función de enlace es logit):
##
## Call:
## glm(formula = cbind(dead, n - dead) ~ logdose, family = binomial)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -60.717 5.181 -11.72 <2e-16 ***
## logdose 34.270 2.912 11.77 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 284.202 on 7 degrees of freedom
## Residual deviance: 11.232 on 6 degrees of freedom
## AIC: 41.43
##
## Number of Fisher Scoring iterations: 4Aquí vemos que el efecto del logaritmo de la dosis es positivo y significativo. Un incremento en la dosis significa un aumento en la probabilidad de que el escarabajo muera. La relación la podemos ver de forma gráfica en la figura 6.4.
pred.x = data.frame(logdose = seq(min(logdose),max(logdose),length.out = 50))
pred = predict(modBin,pred.x,type='response')
plot(logdose,dead/n,xlab='log dosis de disulfuro de carbono gaseoso',ylab='proporción de escarabajos muertos',ylim=c(0,1))
lines(pred.x$logdose,pred,col=2,lwd=2)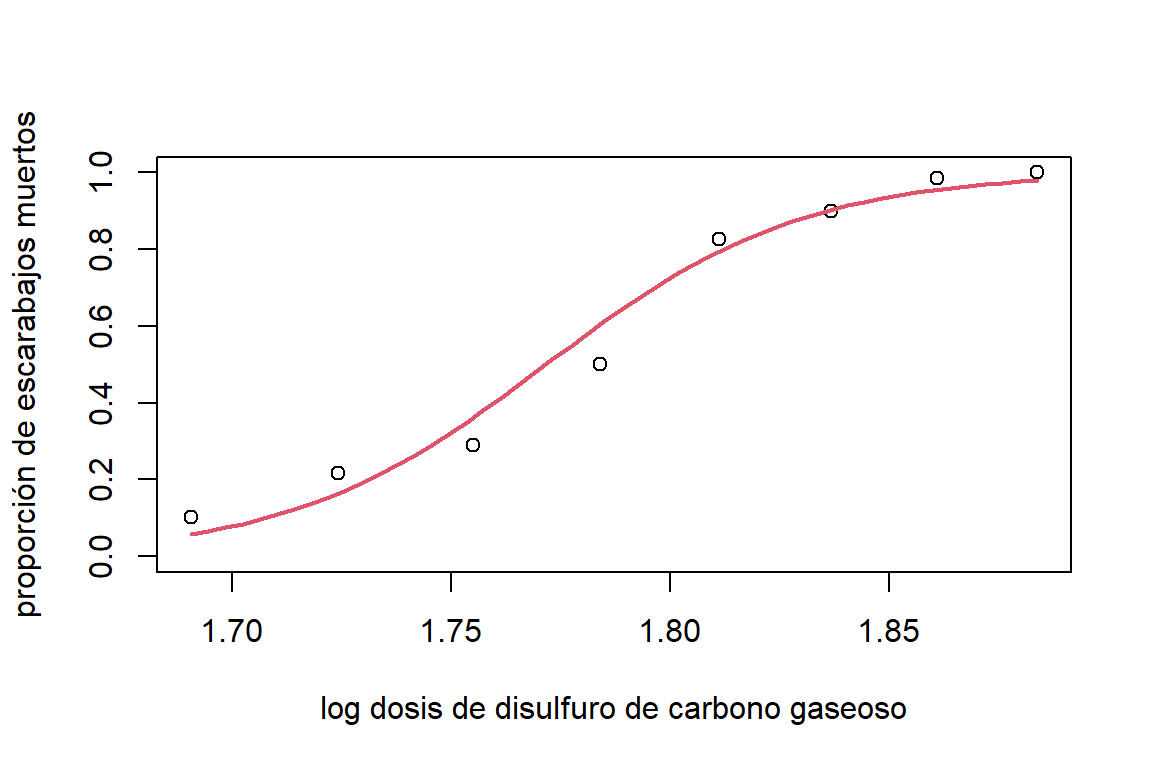
Figure 6.4: Datos de mortalidad de escarabajos. Estimación de la probabilidad de que el escarabajo muera en función del logarítmo de la dosis de disulfuro de carbono gaseoso.
La interpretación de los coeficientes del modelo logístico se hacen a través de los odds ratio. Primero, un odd está definido como:
\[ \mbox{odd}=\frac{P(Y=1)}{P(Y=0)}. \] Es decir, es una razón entre la probabilidad de éxito sobre la probabilidad de fracaso. Por ejemplo, si el odd es igual a dos, estaríamos diciendo que la probabilidad de éxito es el doble de la probabilidad de fracaso. Para el caso del modelo logístico simple, tenemos que:
\[ \text{odd}(x)=\frac{P(Y=1|x)}{P(Y=0|x)}= \frac{\frac{\exp(\beta_0+x\beta_1)}{1+\exp(\beta_0+x\beta_1)}}{1-\frac{\exp(\beta_0+x\beta_1)}{1+\exp(\beta_0+x\beta_1)}} = \exp(\beta_0+x\beta_1). \]
Ahora, los odds ratio están definido como \(\text{OR}=\frac{\text{odd}(x=a+1)}{\text{odd}(x=a)}\). Para el caso del modelo logístico simple tenemos que el OR es:
\[ \mbox{OR}(x)=\frac{\text{odd}(x=a+1)}{\text{odd}(x=a)}=\frac{\exp\left[\beta_{0}+(a+1)\beta_{1}\right]}{\exp(\beta_0+a\beta_1)}=\exp(\beta_1). \]
Por lo tanto, por cada cambio unitario en \(x\), los odds de morir incrementan por un factor de \(exp(\beta_1)\). Por un cambio en \(x\) de \(a\) a \(a+\delta\), tenemos que \(OR=\exp(\delta\beta_1)\).
Para los datos de los escarabajos un cambio unitario en el log dosis es muy grande, por lo que podríamos interpetra \(\beta_1\) usando un aumento en la log dosis mas pequeño, por ejemplo de \(\delta=0.02\):
\[ \exp ( 0.02\times 34.270) = 1.984. 5. \] Por lo que, si el log de la concentración de aumenta en \(0.02\), entonces la probabilidad de que el escarabajo muera aumenta casi el doble.
6.5.2.1 ajuste e interpretación de parámetros del modelo Poisson
Para el ensayo clínico en epilepsia, el modelo propuesto es:
\[
y_i \sim \mbox{Poisson}(\lambda_i), \mbox{ donde } \lambda_i=\exp(\beta_0+\beta_1\text{treat}_i+\beta_2\text{base}_i+\beta_2\text{base}_i\text{treat}_i).
\]
Para el ajuste del modelo usamos la función glm() con el argumento family=poisson:
modPois=glm(seizure.rate~treatment+base+base:treatment,family=poisson,
data =epilepsy4)
summary(modPois)##
## Call:
## glm(formula = seizure.rate ~ treatment + base + base:treatment,
## family = poisson, data = epilepsy4)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.2453159 0.1176157 10.588 <2e-16 ***
## treatmentProgabide -0.3635857 0.1624995 -2.237 0.0253 *
## base 0.0209356 0.0019144 10.936 <2e-16 ***
## treatmentProgabide:base 0.0008523 0.0022778 0.374 0.7083
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 476.25 on 58 degrees of freedom
## Residual deviance: 149.54 on 55 degrees of freedom
## AIC: 345.3
##
## Number of Fisher Scoring iterations: 5Los resultados del ajuste muestran que el número de ataques pre-tratamiento tiene un efecto positivo sobre la media del número de ataques epilépticos. Esto significa que esta es mayor para pacientes con más ataques previos. Mientras que, el tratamiento parece tener un efecto negativo. Es decir, los pacientes que tomaron prograbide tienen una media de ataques epilépticos menor con respecto a los que tomaron el placebo. Finalmente, el efecto interacción es muy pequeño sugiriendo que el efecto del tratamiento no se ve afectado por la frecuencia de los ataques epilépticos que tiene el paciente. La estimación de la media se puede observa de forma gráfica en la Figura 6.5.
y = data.frame(base=seq(min(epilepsy4$base),max(epilepsy4$base),length.out=100),
treatment = factor(1:2, levels = 1:2, labels = levels(epilepsy4$treatment)))
predpois = predict(modPois,y,type='response')
x=seq(min(epilepsy4$base),max(epilepsy4$base),length.out=50)
plot(seizure.rate~base, col=treatment, pch=16,data=epilepsy4,
xlab="ataques pre-tratamiento (x 4 semanas)",
ylab = "ataques post-tratamiento (x 2 semanas)")
lines(x,predpois[order(y$treatment, y$base)[1:50]], lwd = 2)
lines(x,predpois[order(y$treatment, y$base)[51:100]],col=2, lwd = 2)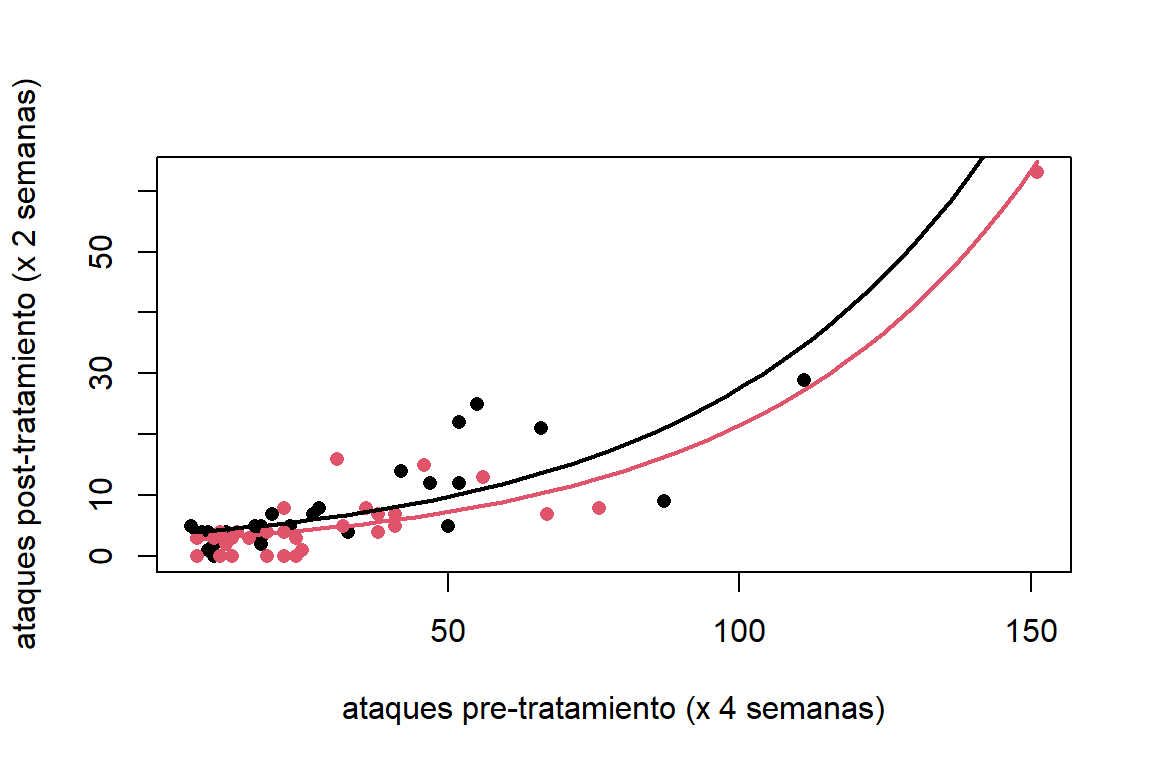
Figure 6.5: Datos de epilepsia. Estimación de la media de ataques epilépticos (por dos semanas) luego de cuatro semanas de tratamiento. La línea negra representa la media de ataques para el grupo placebo, mientras que, la linea roja la media de ataques para el tratamiento con Progabide.
En el modelo Poisson simple, tenemos que \(E(Y|x)=\exp(\beta_0+x\beta_1)\). Si aumentamos a \(x\) en \(\delta\) unidades, tenemos que \(E(Y|x+\delta)=\exp(\beta_0+(x+\delta)\beta_1)\). Ahora si calculamos el logaritmo de la razón de los valores esperados obtenemos que:
\[ \log\left[\frac{E(Y|x=a+\delta)}{E(Y|x=a)}\right]=\delta\beta_1. \]
Por lo tanto, \(\exp(\delta\beta_1)=\frac{E(Y|x=a+\delta)}{E(Y|x=a)}\). Es decir que, \(\exp(\delta\beta_1)\) es una tasa de crecimiento del valor esperado de \(Y\) por un aumento en \(x\) de \(\delta\) unidades.
Por ejemplo, una diferencia de 10 ataques epilépticos pre-tratamiento entre pacientes se asocia con un incremento en la media de ataques post-tratamiento de aproximadamente del 23% (\(\exp(0.0209\times10)\)) para el grupo control.Mientras que para el grupo tratamiento este incremento es del 24% (\(\exp[(0.0209+0.0009)\times10)\))). Note que \(\beta_3\) no es significativo, por lo que esta diferencia no es significativa. Finalmente, el tramiento con Progabida reduce en un poco más del 40% el número de episodios de epilepsia \((\exp(-0.3635857) = 0.695)\).
6.6 Pruebas de hipótesis
Al igual que en los modelos lineales, uno puede estar interesado en realizar pruebas hipótesis sobre los coeficientes del modelo. Por ejemplo, en el estudio sobre epilépsia estamos interesados en evaluar si hay un efecto significativo del tratamiento sobre los ataques epilépticos. Esto es: \[ \qquad H_0:\beta_1=\beta_3=0. \] Si rechazamos \(H_0\) podemos concluir que el tratamiento con Progabida tiene un efecto sobre el número de ataques epilépticos. Particularmente, si \(\beta_1 < 0\), este fármaco reduce los episodios.
Suponga que tenemos un modelo con el siguiente predictor lineal: \[ \eta = \boldsymbol x_{1}'\boldsymbol \beta_1+\boldsymbol x_{2}'\boldsymbol \beta_2, \] donde \(\boldsymbol x_{1 }= (1,x_{11},\ldots,x_{1,q-1})'\) y \(\boldsymbol x_{2}= (1,x_{21},\ldots,x_{2,p-q})'\) son vectores de covariables; \(\boldsymbol \beta_1\) y \(\boldsymbol \beta_2\) son vectores de coeficientes de dimensiones \(q\) y \(p-q\), respetivamente. Ahora, planteamos el siguiente sistema de hipótesis: \[ \qquad H_0:\boldsymbol \beta_2=\boldsymbol 0\qquad H_1:\boldsymbol \beta_2 \ne \boldsymbol 0. \] Para estimadores basados en verosimilitud, podemos utilizar tres métodos diferentes: la prueba de razón de verosimilitud, la prueba del score o la prueba de Wald.
6.6.1 Método de razón de verosimilitud
La idea de este método es comparar la verosimilitud bajo dos condiciones: (\(L_0\)) la máxima alcanzada bajo \(H_0\) (es decir, asumiendo que \(\boldsymbol \beta_2=\boldsymbol 0\)) y (\(L_1\)) la evaluada en la estimación máximo verosimil (es decir, \(L(\widehat{\boldsymbol \beta})\)). El estadístico de prueba usado es: \[ LR = 2\log \left( \frac{L(\widehat{\boldsymbol \beta})}{L(\widehat{\boldsymbol \beta}_0)} \right) = 2 (\ell_1 - \ell_0). \] Asumiendo que \(H_0\) es cierta, asintóticamente tenemos que \(LR \sim \chi^{2}_{p-q}\). Por lo que, rechazamos \(H_0\) con un nivel de significancia de \(\alpha\), si \(LR > \chi^{2}_{1-\alpha,p-q}\).
6.6.2 Método de Wald
Asintóticamente, tenemos que \(\widehat{\boldsymbol \beta}\sim N[\boldsymbol \beta,\boldsymbol I(\boldsymbol \beta)^{-1}]\). por lo tanto se tiene que: \[ (\hat{\boldsymbol \beta}-\boldsymbol \beta)'\boldsymbol I(\boldsymbol \beta)(\hat{\boldsymbol \beta}-\boldsymbol \beta)\sim\chi^2_{p}. \] Entonces, para probar \(H_0: \boldsymbol \beta_2 = \boldsymbol \beta_2^{0}\), se puede utilizar el siguiente estadístico de prueba: \[ W = \left(\widehat{\boldsymbol \beta}_2-\boldsymbol \beta_2^{0}\right)'\left[V\left(\widehat{\boldsymbol \beta}_2\right)\right]^{-1}\left(\widehat{\boldsymbol \beta}_2-\boldsymbol \beta_2^0\right). \] Si \(H_0\) es cierta, entonces \(W \sim \chi^2_{p-q}\). Por lo que, rechazamos \(H_0\) con un nivel de significancia de \(\alpha\), si \(W > \chi^{2}_{1-\alpha,p-q}\).
6.6.2.1 Ejemplo ataques epilépticos
En este caso, podríamos plantear el siguiente sistema de hipótesis: \[ \qquad H_0:\beta_1=\beta_3=0 \qquad H_1: \beta_1=0 \mbox{ o } \beta_3=0. \] Aquí, \(H_0\) indica que no hay ningún efecto del tratamiento para la epilépsia (no es estadísticamente diferente al placebo). La prueba de razón de verosimilitud se puede implementar de las siguiente forma:
## Analysis of Deviance Table
##
## Model 1: seizure.rate ~ base
## Model 2: seizure.rate ~ treatment + base + base:treatment
## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1 57 159.94
## 2 55 149.54 2 10.405 0.005502 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Este resultado, complementado con los anteriores, sugiere que hay un efecto del tratamiento. Es decir, el Progabida tiene un efecto significativo para reducir los ataques epilépticos.
La prueba de Wald la podemos implementar de la siguiente forma:
##
## Adjuntando el paquete: 'aod'## The following objects are masked from 'package:faraway':
##
## rats, salmonella## Wald test:
## ----------
##
## Chi-squared test:
## X2 = 10.3, df = 2, P(> X2) = 0.0057Estos resultados son similares a los observados con la prueba de razón de verosimilitud y llegamos a la misma conclusión.
6.7 intervalos de confianza
A partir de los estadísticos de prueba anteriores se pueden encontrar intervalos de confianza para \(\boldsymbol \beta\). Por ejemplo usando el estadístico de Wald:
\[ \widehat{\beta}_j\pm z_{\alpha/2}\sqrt{V(\widehat{\beta}_j)}. \]
Otra alternativa es a partir de los perfiles de log-verosimilitud, el intervalo del \((1-\alpha)\)% de confianza para \(\beta_j\) está definido a partir de los valores de \(\beta^0_j\) que satisfacen:
\[ -2[\ell(\widehat{\boldsymbol \beta})-\ell(\widehat{\boldsymbol \beta}^{0})]<\chi^2_{1-\alpha,1}, \]
donde \(\ell(\widehat{\boldsymbol \beta}^{0})\) es la log-verosimilitud donde \(\beta_j\) está restringido a los valores de \(\beta_j^0\).
6.7.1 Intervalo de confianza para la media
Dado que \(\widehat{\eta}_0=\boldsymbol x_0'\widehat{\boldsymbol \beta}\) ,por lo tanto (asintóticamente):
\[ \widehat{\eta}_0\sim N[\boldsymbol x_0'\boldsymbol \beta,\boldsymbol x_0'\boldsymbol I(\boldsymbol \beta)^{-1}\boldsymbol x_0]. \]
Entonces un intervalo de confianza para \(\eta_0\) es:
\[ \widehat{\eta}_0\pm z_{\alpha/2}\sqrt{\boldsymbol x_0'I(\widehat{\boldsymbol \beta})^{-1}\boldsymbol x_0}. \]
Para encontrar el intervalo de confianza para \(\mu_i\), se hace la transformación \(g^{-1}\) a los límites de confianza.
6.7.1.1 Ejemplo mortalidad de escarabajos
La estimación de la probabilidad de que el escarabajo muera se puede observar en la Figura 6.6.
pred.link = predict(modBin,newdata = pred.x,type='link',se.fit = T)
lim.sup = faraway::ilogit(pred.link$fit + qnorm(0.975)*pred.link$se.fit)
lim.inf = faraway::ilogit(pred.link$fit - qnorm(0.975)*pred.link$se.fit)
plot(logdose,dead/n,xlab='log dosis',ylab='proporción de escarabajos muertos',ylim=c(0,1))
lines(pred.x$logdose,pred)
lines(pred.x$logdose,lim.sup, col=2)
lines(pred.x$logdose,lim.inf, col=2)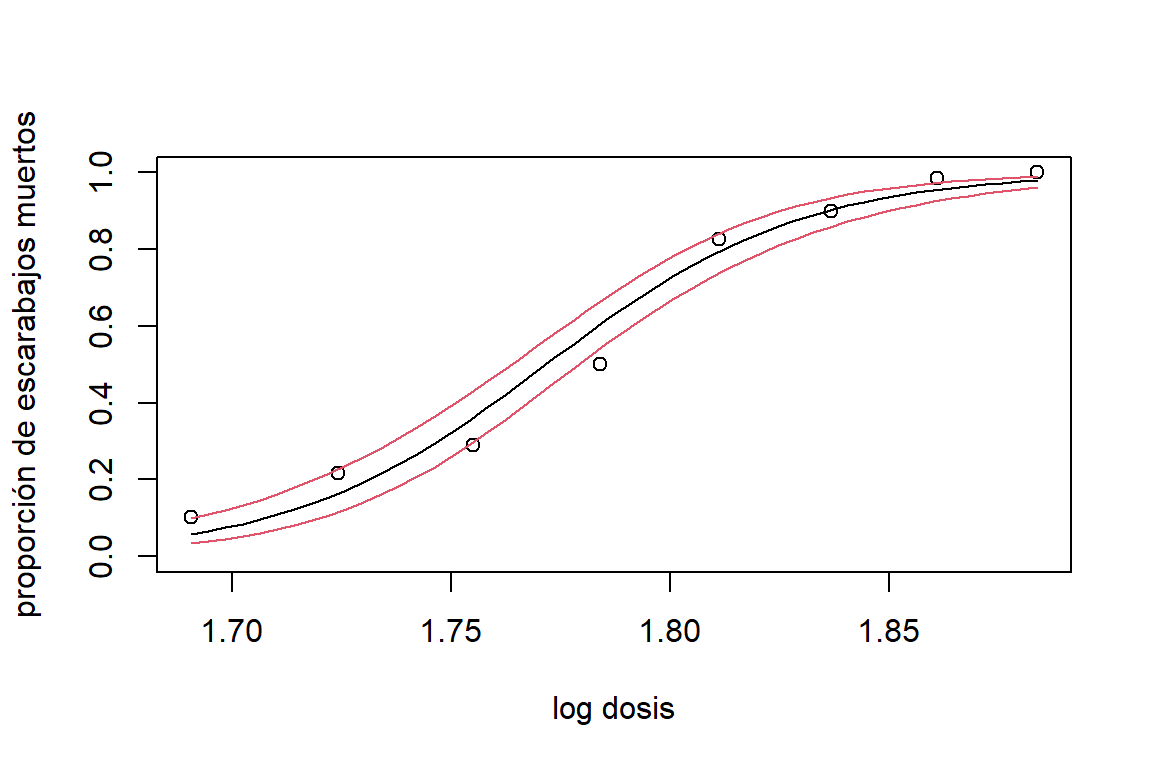
Figure 6.6: Datos de mortalidad de escarabajos. Intervalo del 95% de confianza para la probabilidad de que el escarabajo muera.
6.7.1.2 Ataques epilépticos
Los intervalos del 95% de confianza para los parámetros del modelo son:
## 2.5 % 97.5 %
## (Intercept) 1.009325667 1.470661654
## treatmentProgabide -0.682237759 -0.044653101
## base 0.017137251 0.024649428
## treatmentProgabide:base -0.003594654 0.005341111Aquí vemos que el efecto del tratamiento está entre \(-0.7\) y \(-0.04\). Es decir, que la reducción del número de ataques epilépticos está a una tasa entre el 0.51 y 0.95. Mientras que, como ya se mencionó antes, el efecto interacción no tiene un aporte significativo.
La media del número de ataques epiléptico por dos semanas se puede observar en la Figura 6.7. Se puede ver que las estimaciones de la media para el grupo tratamiento es inferior que para el grupo control.
predx1 = data.frame(base=seq(6,151,length.out = 100),treatment='placebo')
predx2 = data.frame(base=seq(6,151,length.out = 100),treatment='Progabide')
predy1 = predict(modPois,newdata = predx1,type='response')
predy2 = predict(modPois,newdata = predx2,type='response')
predy1Link = predict(modPois,newdata = predx1,type='link',se.fit = T)
predy2Link = predict(modPois,newdata = predx2,type='link',se.fit = T)
lwr1 = exp(predy1Link$fit - qnorm(0.975)*predy1Link$se.fit)
upr1 = exp(predy1Link$fit + qnorm(0.975)*predy1Link$se.fit)
lwr2 = exp(predy2Link$fit - qnorm(0.975)*predy2Link$se.fit)
upr2 = exp(predy2Link$fit + qnorm(0.975)*predy2Link$se.fit)
plot(epilepsy4$base,epilepsy4$seizure.rate,
ylab='# ataques epilépticos (4ta semana)',
xlab='# ataques epilépticos (pre tratamiento)',
col=as.double(epilepsy4$treatment))
lines(predx1$base,predy1,lwd=2)
lines(predx1$base,predy2,col=2,lwd=2)
lines(predx1$base,lwr1,lty=2)
lines(predx1$base,upr1,lty=2)
lines(predx2$base,lwr2,lty=2,col=2)
lines(predx2$base,upr2,lty=2,col=2)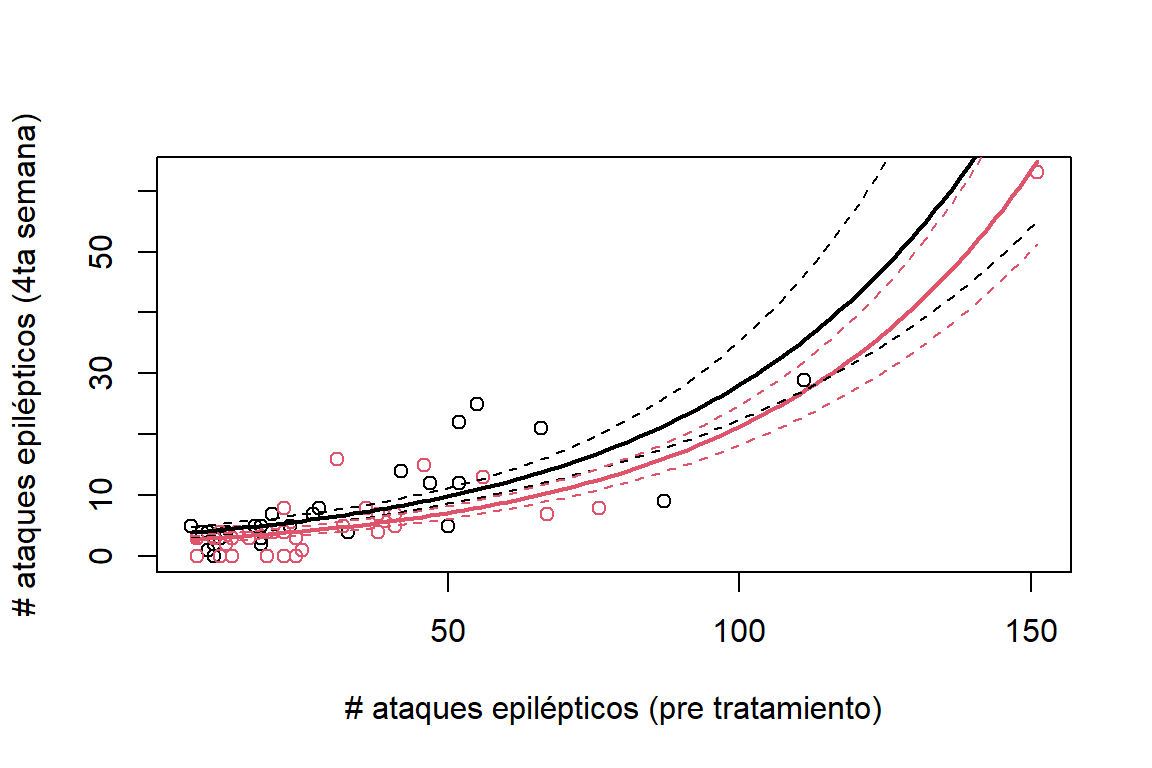
Figure 6.7: Datos de epilépsia. Estimación de la media de ataques epilépticos por dos semanas en el grupo placebo (línea negra) y el grupo tratamiento (línea roja).
6.8 Devianza
Considere un GLM con observaciones \(\boldsymbol y_i=(y_1,...,y_n)\). Sea \(ℓ(\widehat{\boldsymbol \mu})\) la log-verosimilitud (expresada en función de \(\boldsymbol \mu\)) evaluada en el MLE. La máxima verosimilitud que se puede alcanzar corresponde a \(ℓ(\boldsymbol y)\) (un modelo con ajuste perfecto \(y_i=\mu_i\)). A este último se le conoce como el modelo saturado. La Devianza compara el modelo propuesto contra el modelo saturado de la siguiente manera:
\[\begin{equation} \begin{split} D &=- 2 \log \left[ \frac{L(\widehat{\boldsymbol \mu})}{L(\boldsymbol y)} \right] = -2[\ell(\hat{\boldsymbol \mu})-\ell(\boldsymbol y)] \\ &= 2\sum_{i=1}^n[y_i\widetilde{\theta}_i-b(\widetilde{\theta}_i)]/a(\phi) - \sum_{i=1}^n[y_i\widehat{\theta_i}-b(\widehat{\theta_i})]/a(\phi), \end{split} \end{equation}\] donde \(\widetilde{\theta}_i\) corresponde a la estimación de \(\theta_i\) en el modelo saturado \((\widetilde{\mu}_i=y_i)\). Dado que, \(\ell(\boldsymbol y) \geq \ell(\hat{\boldsymbol \mu})\), entonces \(D \geq 0\). Por lo que, si el ajuste propuesto es pobre, se espera que \(D\) sea grande.
Modelo binomial: Para el modelo binomial, la devianza está determinada por: \[ D=2\sum_{i=1}^n\left[y_i\log \left(\frac{y_i}{\widehat{\mu}_i}\right)+(n_i-y_i)\log\left(\frac{n_i-y_i}{n_i-\widehat{\mu}_i}\right)\right], \]
donde \(\widehat{\mu}_i=n_i\widehat{\pi}_i.\)
Modelo Poisson: Para el modelo Poisson, la devianza está definida como: \[ D=2\sum_{i=1}^ny_i\log\left(\frac{y_i}{\widehat{\mu}_i}\right), \quad \text{donde} \quad \widehat{\mu}_i=\widehat{\lambda}_i. \]
Modelo normal: Mientras que, para el modelo lineal es: \[ D=2\sum_{i=1}^n\left(y_i-\widehat{\mu}_i\right)^2. \]
6.8.1 El estadístico chi-cuadrado de Pearson
Otro indicador de calidad del modelo es el estadístico chi-cuadrado de Pearson, definido como:
\[ X^2=\sum_{i=1}^n\frac{\left(y_i-\widehat{\mu}_i\right)^2}{v(\widehat{\mu}_i)}. \] Para el modelo binomial, tenemos que: \[ X^2=\sum_{i=1}^n\frac{(y_i-n_i\hat{\pi}_i)^2}{n_i\hat{\pi}_i(1-\hat{\pi})}. \]
Para el modelo Poisson es: \[ X^2=\sum_{i=1}^n\frac{(y_i-\widehat{\mu}_i)^2}{\widehat{\mu}_i}. \]
6.9 Bondad de ajuste
Tanto \(D\) como \(X^2\) se pueden utilizar para evaluar la bondad del ajuste. Por lo que se podría plantear las siguientes hipótesis: \(H_0\) indica que el modelo ajusta bien a los datos, y \(H_1\) lo contrario. Por ejemplo, en el caso de un modelo logístico:
\[ H_0:\mbox{logit}(\pi_i)=\x_i\boldsymbol \beta. \]
Si \(H_0\) es cierta, entonces \(D\) y \(X_2\) siguen una distribución \(\chi_2\) con \((n - p)\) grados de libertadad. Sin embargo, está aproximación es buena solo si se cuenta con datos agrupados.
Mortalidad de escarabajos Para el modelo de mortalidad de escarabajos, los valores de la devianza y el \(\chi^2\) de Pearson son:
## [1] 0.08145881## [1] 0.1235272Los datos de epilepsia no están agrupados, por lo tanto esta prueba de bondad de ajuste no se puede utilizar.
6.10 Selección de variables
La selección de variables se puede realizar de la misma forma que en los LMs basándose en indicadores como el AIC y BIC (o alguna modificación de ellos). El primero está definido como: \[ \text{AIC}=-2\ell_M+2p, \] donde \(\ell_M\) es la verosimilitud alcanzada con el modelo propuesto y \(p\) el número de parámetros. El segundo indicador como: \[ \text{BIC}=-2\ell_M+p\log(n). \] En ambos casos, entre mas pequeños sean estos indicadores mejor es el modelo.