Capítulo 4 Transformaciones y mínimos cuadrados ordinarios

Ejemplo 1. Datos de la ONU

La base de datos UN11 de la librería alr4 contiene las siguientes estadísticas de varios miembros de las naciones unidas (y otras regiones independientes) durante los años 2009-2011:

  • fertility: Número esperado de nacidos vivos por mujer.
  • ppgdp: producto nacional bruto per cápita (PNB, en dólares).
  • Purban: el porcentaje de la población que vive en un área urbana.
  • lifeExpF: esperanza de vida femenina (años).

El objetivo del estudio es ver la relación entre la fertilidad con las otras variables. Por ahora, empecemos con un modelo de la fertilidad en función del producto nacional bruto y el porcentaje de población urbana.

La Figura 4.1 muestra la relación entre las variables. Aquí vemos que ambas covariables tienen una relación negativa con la fertilidad. Note, además, que la relación con el producto nacional bruto no es lineal. Esto último podría traer problemas a la hora de ajustar un modelo lineal.

library(alr4)
data("UN11")
pairs(UN11[,-c(1:2,5)])
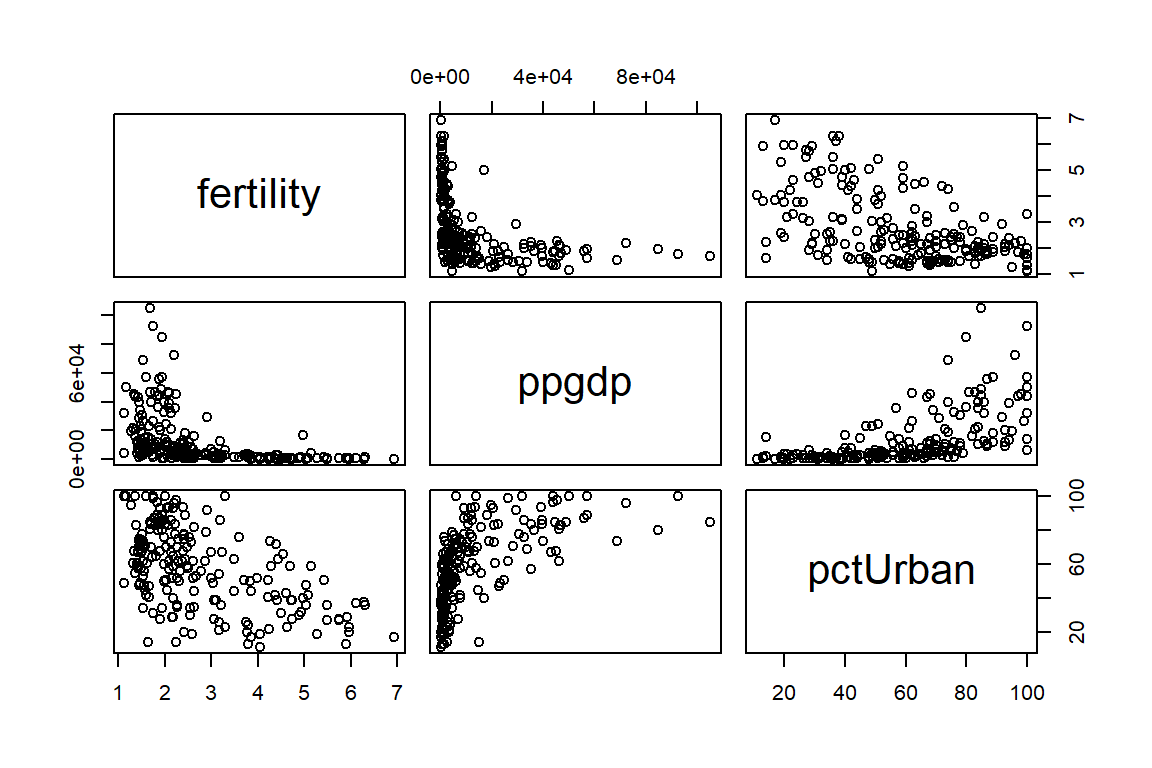
Datos de la ONU. Relación entre las variables.

Figure 4.1: Datos de la ONU. Relación entre las variables.

Por ahora consideremos solamente el PNB y el % de población en área urbana como covariables. Por lo tanto, el modelo propuesto es el siguiente: \[ \mbox{fertility}_{i} = \beta_{0} + \beta_{1}\mbox{ppgdp}_{i} + \beta_{2}\mbox{pctUrban}_{i} + \varepsilon_{i}, \] donde \(\varepsilon_{i}\sim N(0,\sigma^{2})\) y \(cov(\varepsilon_{j},\varepsilon_{k})=0\).

Luego de ajustar el modelo se procede a hacer un análisis de residuos. El gráfico de los residuos estudentizados (Figura 4.2 muestra que el ajuste presenta problemas de no linealidad y heterocedasticidad. En la Figura 4.3 de los residuos parciales podemos observar que estos problemas se deben a la covariable PNB.

mod.UN11 = lm(fertility~ppgdp+pctUrban,data=UN11)
library(MASS)
res.UN11 = studres(mod.UN11)
plot(mod.UN11$fitted.values,res.UN11,
     xlab='valores ajustados',ylab='residuos estudentizados')
lines(lowess(res.UN11~mod.UN11$fitted.values),col=2)
abline(h=0,lty=2)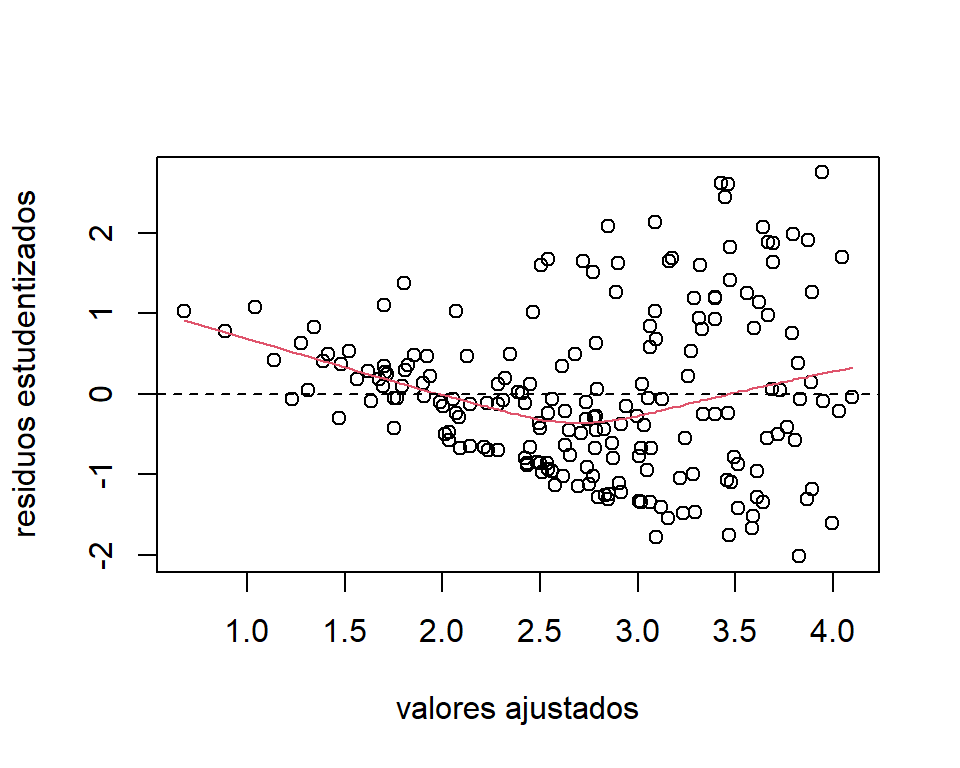
Datos de la ONU. Gráfico de los residuos estudentizados.

Figure 4.2: Datos de la ONU. Gráfico de los residuos estudentizados. 

library(car)
crPlots(mod.UN11,main='')
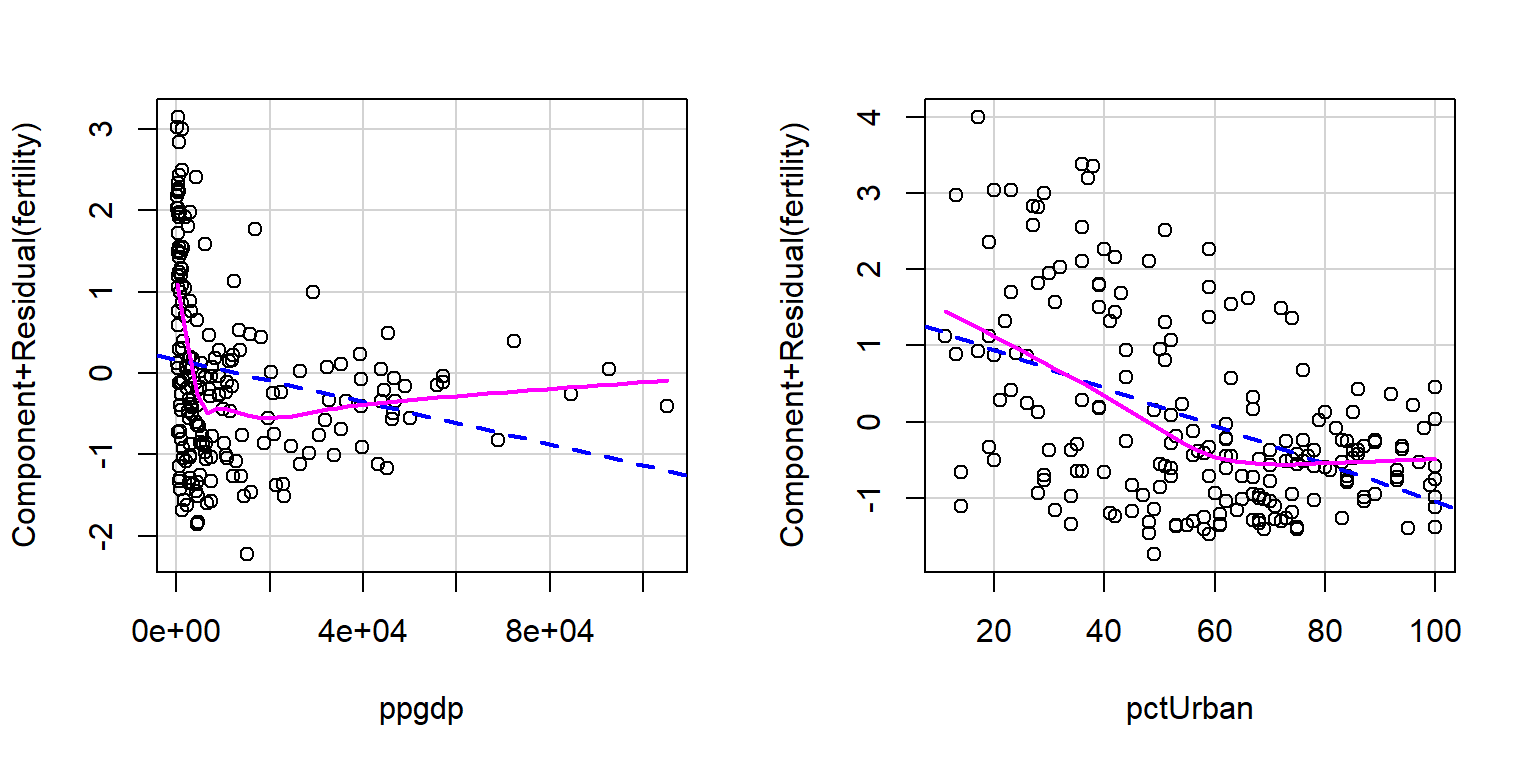
Datos de la ONU. Gráfico de los residuos parciales.

Figure 4.3: Datos de la ONU. Gráfico de los residuos parciales.

Ejemplo 2. Datos de educación

La base de datos education de la librería robustbase contiene información sobre gastos en educación de 50 estados de los EEUU en el año 1975. Las variables observadas son:

  • Y: gasto per cápita en educación pública (dólares, proyectado para 1975).
  • X1: número de residentes en áreas urbanas en 1970 (en miles).
  • X2: ingreso per cápita en 1973 (en miles dolares).
  • X3: número de residentes menores de 18 años en 1974 (en miles)

La relación entre las variables se observa en la Figura 4.4. Se observa una relación positiva aproximadamente lineal entre la variable respuesta y las covariables, aunque no es tan fuerte con la covariable número de residentes menores de 18 años. Además, vemos que hay por lo menos un posible valor atípico.

library(robustbase)
data("education")
education$X2 = education$X2/1000 # cambio de unidad de medida (miles de dolares)
pairs(education[,c(6,3:5)])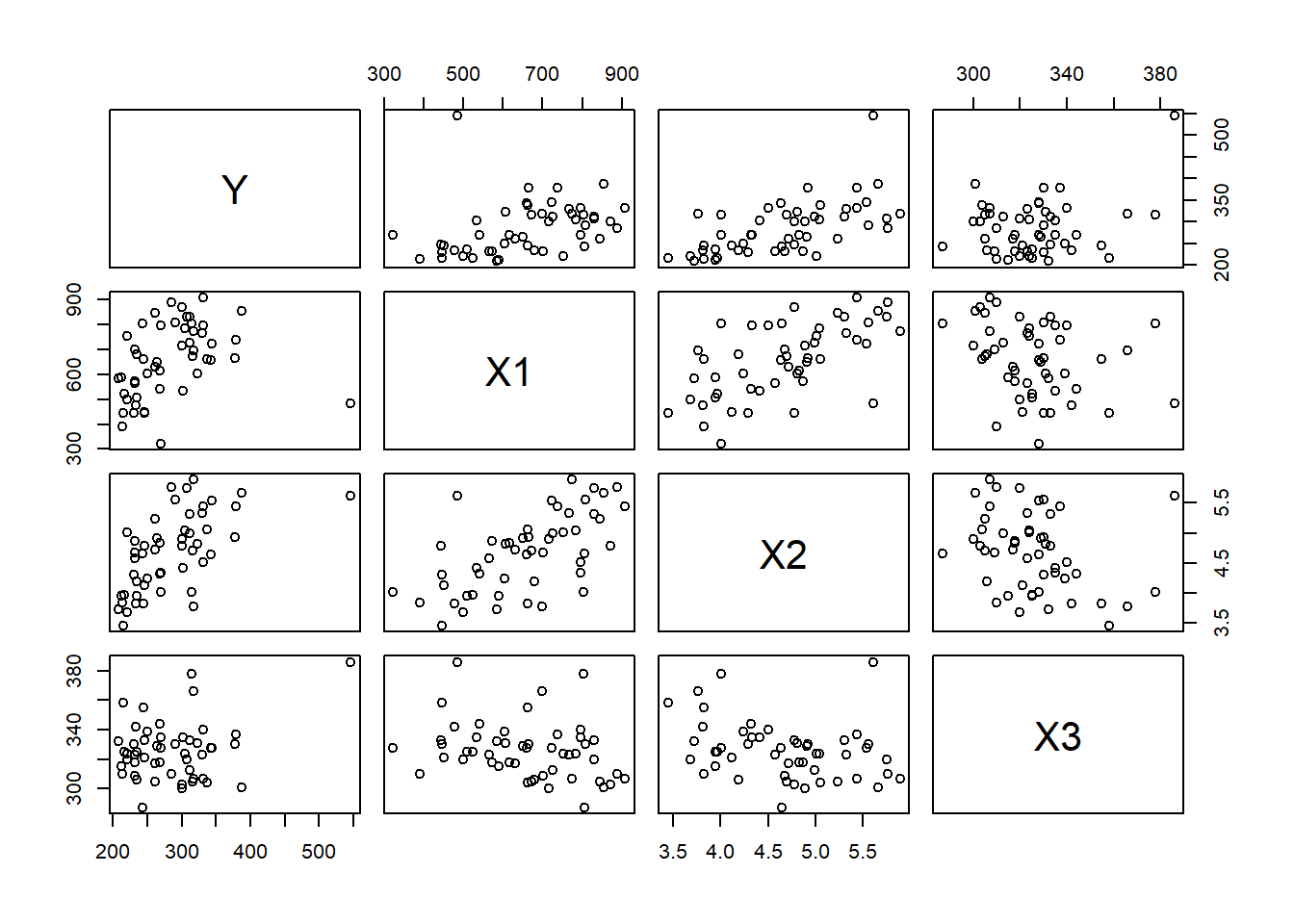
Datos de educación. Relación entre las variables.

Figure 4.4: Datos de educación. Relación entre las variables.

El objetivo es ajustar un modelo de regresión para el gasto per cápita en educación pública en función de las demás variables: \[ Y_{i} = \beta_{0} + \beta_{1}\mbox{X1}_{i} + \beta_{2}\mbox{X2}_{i}+ \beta_{3}\mbox{X3}_{i} + \varepsilon_{i}, \] donde \(\varepsilon_{i}\sim N(0,\sigma^{2})\) y \(cov(\varepsilon_{j},\varepsilon_{k})=0\).

Antes de hacer inferencias sobre el modelo hacemos un análisis de los residuos. La Figura 4.5 exhibe el gráfico de los residuos estudentizados. Aunque la relación entre la variable respuesta y covariables es aproximadamente lineal, hay presencia de heterocedasticidad. La variabilidad de los residuos aumenta con los valores ajustados.

mod.educ = lm(Y~X1+X2+X3,data=education)
library(MASS)
res.educ = studres(mod.educ)
par(mfrow=c(1,2))
plot(mod.educ$fitted.values,res.educ,
     xlab='valores ajustados',ylab='residuos estudentizados')
lines(lowess(res.educ~mod.educ$fitted.values),col=2)
abline(h=0,lty=2)
plot(mod.educ$fitted.values,abs(res.educ),
     xlab='valores ajustados',ylab='| residuos estudentizados |')
lines(lowess(abs(res.educ)~mod.educ$fitted.values),col=2)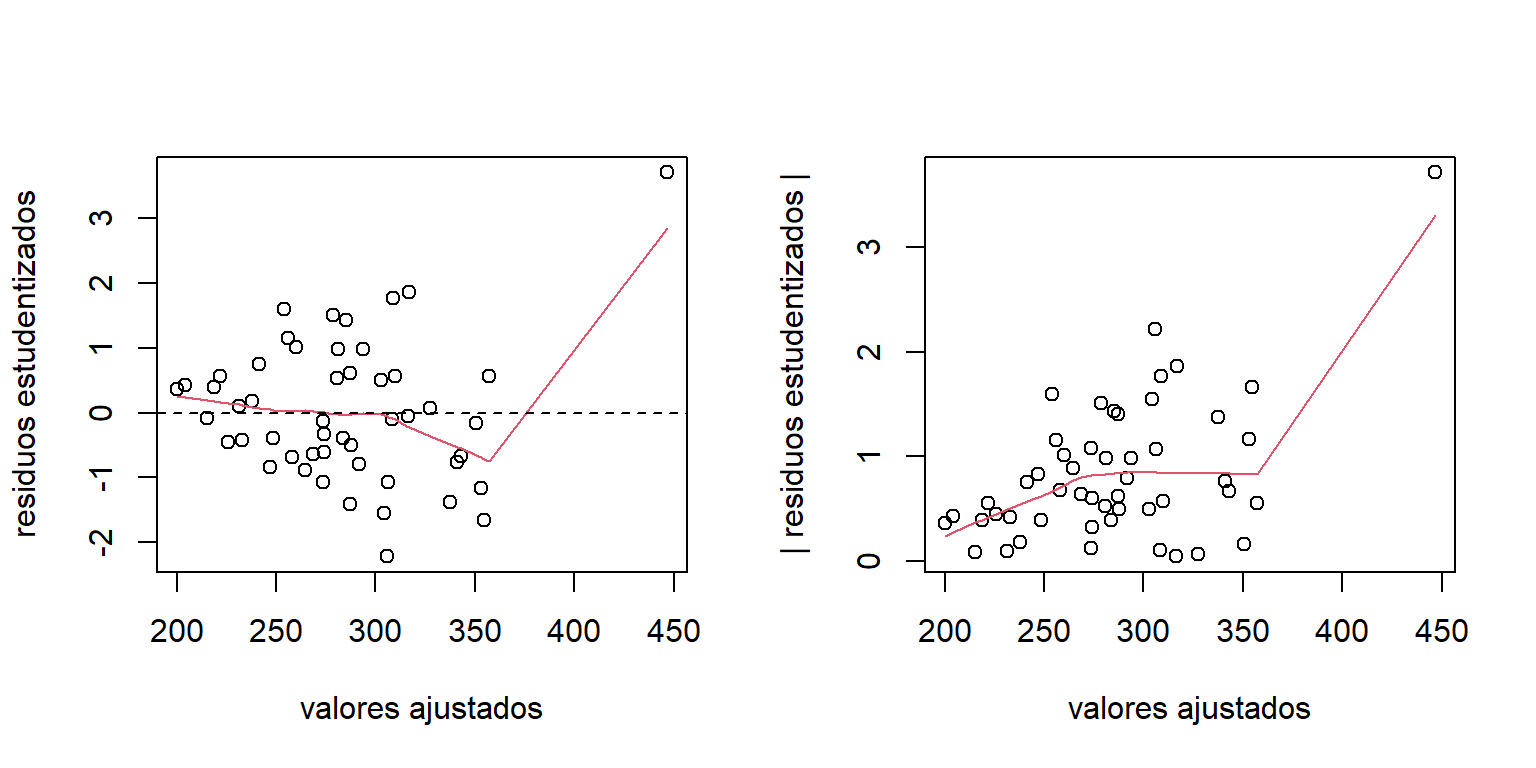
Datos de educación. Gráficos de los residuos estudentizados.

Figure 4.5: Datos de educación. Gráficos de los residuos estudentizados.

Dado que los modelos ajustados presentan desviaciones considerables de los supuestos asumidos, las inferencias que se hagan pueden ser invalidas. Por lo tanto, en este capítulo presentaremos dos herramientas para la corrección de estos problemas: (1) transformación de variables (incluyendo la transformación de Box-Cox) y (2) mínimos cuadrados ponderados.

4.1 Transformación de los datos

Los objetivos de realizar transformaciones sobre los datos son:

  • linealizar la relación de las variables,
  • estabilizar la varianza,
  • y corregir la normalidad.

Las transformaciones pueden hacerse sobre la variable respuesta, las covariables, o ambas.

La desventaja de hacer transformaciones es que la interpretación del modelo estimado, así como las inferencias, se hacen sobre las variables transformadas, y no en su escala original.

4.1.1 Transformaciones para linealizar el modelo

Recordemos que el modelo lineal asume que la relación entre la media y las covariables es aproximadamente lineal. En algunos casos, dada la naturaleza de los datos, este supuesto puede ser violado. Por lo tanto, para seguir utilizando la metodología de los modelos lineales, es posible linealizar funciones no-lineales por medio de transformaciones.

Algunas de estas funciones linealizables y su representación gráfica, se muestran en la Tabla 4.1 y Figura 4.6, respectivamente. Por ejemplo, considere que el modelo generador de los datos es: \[ y_{i} = \beta_{0}\exp\left(\beta_{1}x_{i1} \right)\varepsilon_{i}. \] Ver figura 4.6(b). Esta relación no lineal se puede linealizar aplicando una transformación logaritmica a ambos lados:

\[ \log y_{i} = y_{i}^{*} = \log \left[ \beta_{0}\exp\left(\beta_{1}x_{i} \right)\varepsilon_{i} \right] = \log \beta_{0} + \beta_{1}x_{i} + \log\varepsilon_{i}. \] Note que estaríamos asumiendo que \(\log\varepsilon_{i}\) está normalmente distribuido. Para que esto sea cierto, \(\varepsilon_{i}\) debe seguir una distribución log-normal.

Table 4.1: Funciones linealizables
Función Transformación Forma lineal
(a) \(y = \beta_{0}x^{\beta_{1}}\) \(y^{*}= \log(y), x^{*} = \log(x)\) \(y^{*} = \log(\beta_{0}) + \beta_{1} x^{*}\)
(b) \(y = \beta_{0}e^{\beta_{1}x}\) \(y^{*}= \log(y)\) \(y^{*} = \log(\beta_{0}) + \beta_{1} x\)
(c) \(y = \beta_{0}+\beta_{1}ln(x)\) \(x^{*}= \log(x)\) \(y^{*} = \beta_{0} + \beta_{1} x^{*}\)
(d) \(y = \frac{x}{\beta_{0}x+\beta_{1}}\) \(x^{*}= \frac{1}{x}, y^{*}= \frac{1}{y}\) \(y^{*} = \beta_{0} - \beta_{1} x^{*}\)
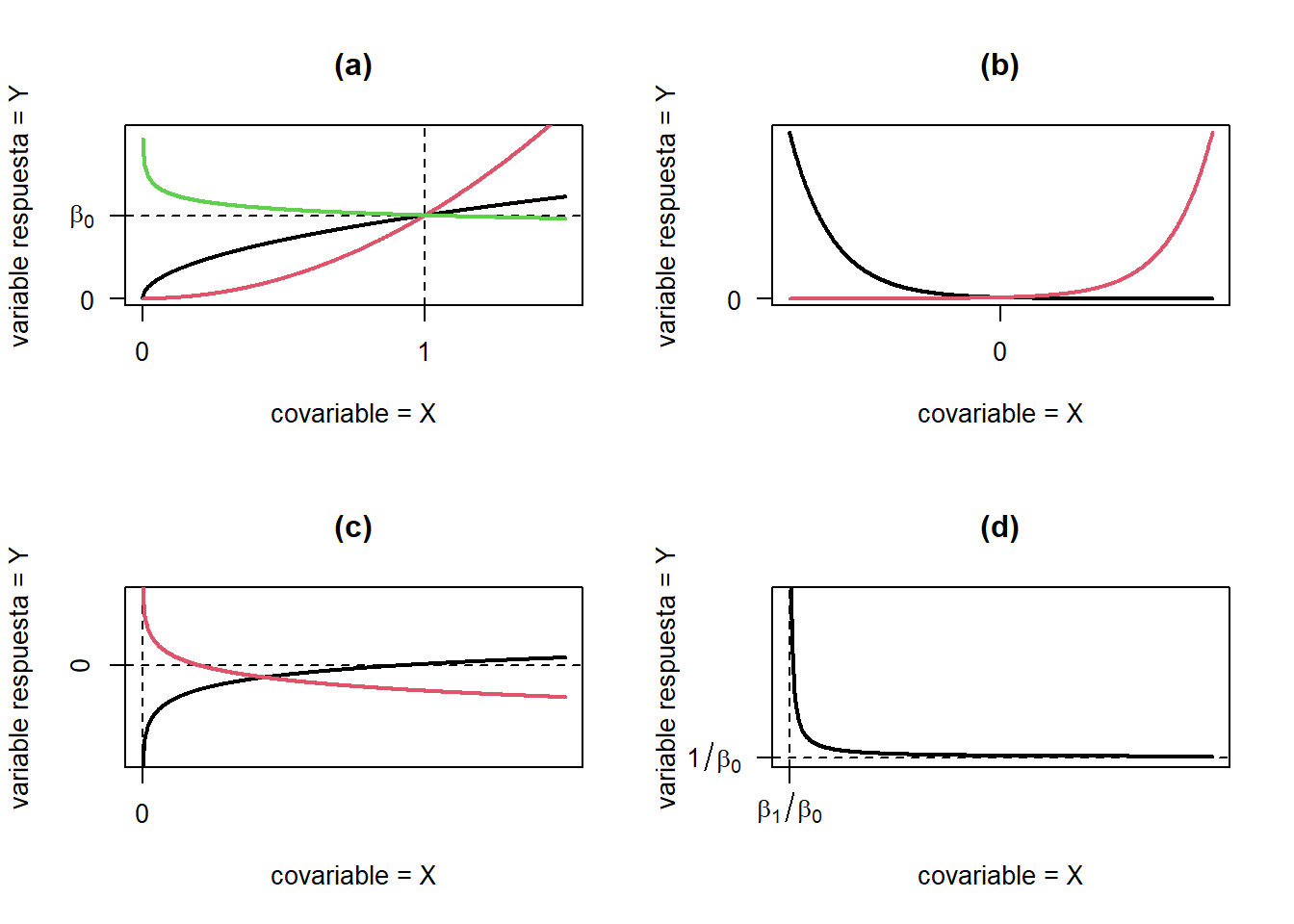
Diferentes patrones linealizables.

Figure 4.6: Diferentes patrones linealizables.

4.1.2 Transformaciones para estabilizar la varianza

Un caso frecuente es que la variable respuesta sigue una distribución de probabilidad en la que la varianza se relaciona en forma funcional con la media: \[ V(Y|X=x) = \sigma^2 g[E(Y|X=x)]. \] Por ejemplo, en la distribución Poisson, la varianza es igual a la media. Algunas transformaciones comunes para estabilizar varianza se muestran en la Tabla 4.2 (Behar 2002).

Table 4.2: Algunas transformaciones para estabilizar la varianza
Relación entre \(\sigma^{2}\) y \(E(Y)\) Transformación
\(\sigma^{2} \propto C\) \(y^{*}=y\)
\(\sigma^{2} \propto E(y)\) \(y^{*}=\sqrt{y}\)
\(\sigma^{2} \propto E(y)[1-E(y)]\) \(y^{*}=\sin^{-1}\sqrt{y} (0 \leq y_{i} \leq 1)\)
\(\sigma^{2} \propto E(y)^{2}\) \(y^{*}=\log y\) o también \(y^{*}=\log (y+1)\) (si \(y \geq 0\))
\(\sigma^{2} \propto E(y)^{3}\) \(y^{*}=\frac{1}{\sqrt{y}}\)
\(\sigma^{2} \propto E(y)^{4}\) \(y^{*}=\frac{1}{y}\)

Algunas consideraciones cuando se hacen transformaciones sobre las variables:

  • Transformaciones pueden ser sugeridas por experiencia (o teoría). En otros casos, la selección se hace empíricamente.
  • Luego de realizar las transformaciones se debe verificar si el modelo transformado cumple los supuestos.
  • El estimador de MCO tiene propiedades de mínimos cuadrados con respecto a los datos transformados.
  • Las predicciones son sobre las respuestas transformadas, no las originales. Devolverse a la variable respuesta original no es fácil. Recordemos que \[ E[g(y)] \neq g[E(y)]. \] Al aplicar la transformación inversa a las predicciones de la respuesta transformada estamos estimando la mediana, y no la media. Por otro lado, a las estimaciones por intervalos de confianza si se les puede aplicar la transformación inversa. Esto porque los percentiles no se ven afectados por transformaciones.

Datos de la ONU. Transformación para linealizar los datos

Al realizar un análisis de residuos del ajuste del modelo para los datos de la ONU, vimos que hay una relación no-lineal entre la fertilidad y las dos covariables propuestas. Particularmente, esto se debe a la covariable producto nacional bruto.

Por lo tanto, podemos aplicar una transformación logarítmica tanto a la variable respuesta, así como la covariable producto nacional bruto. En la Figura 4.7 vemos como al aplicar esta transformación se linealiza la relación.

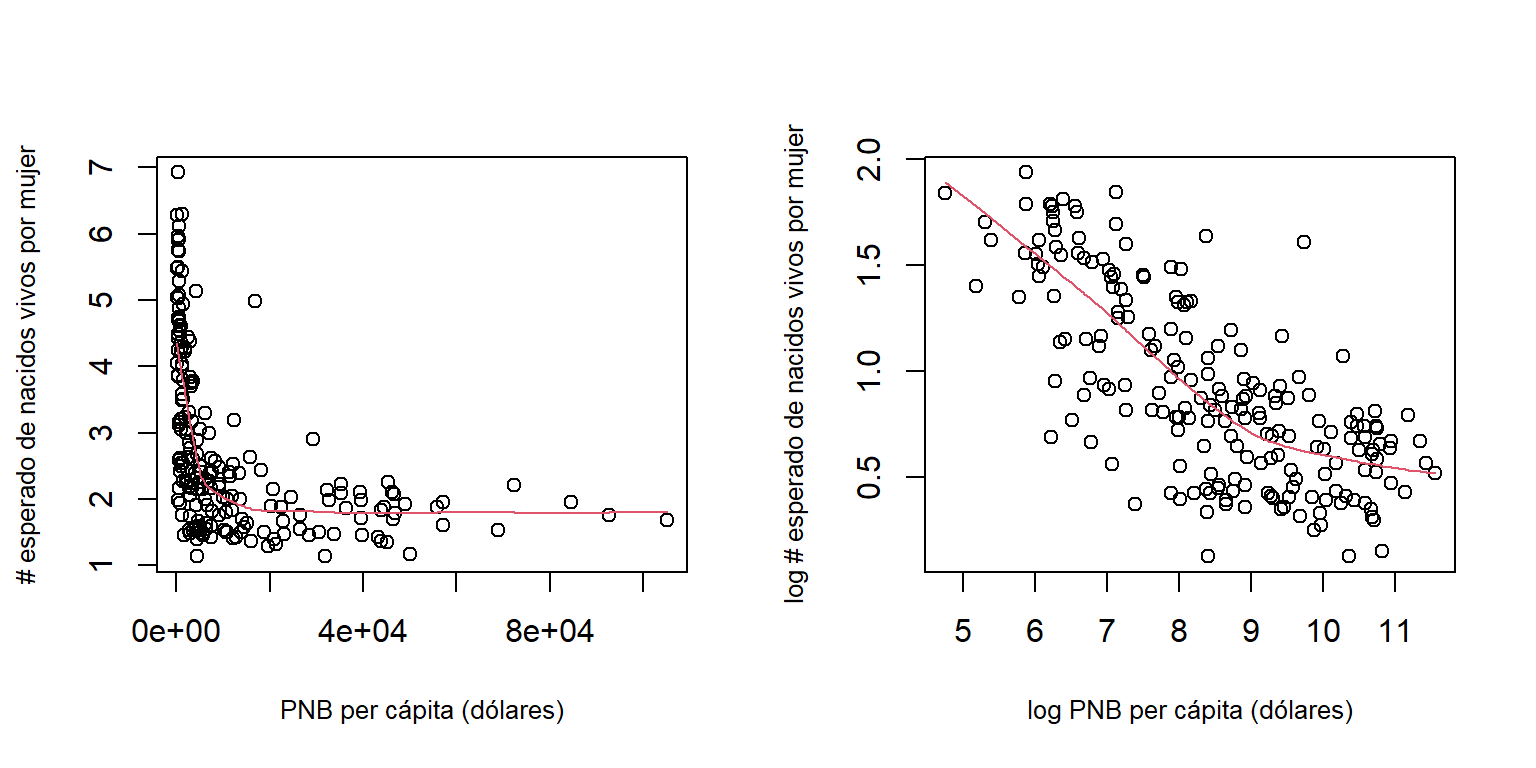
Datos de la ONU. Relación entre las variables.

Figure 4.7: Datos de la ONU. Relación entre las variables.

Producto de esta transformación, se propone el siguiente modelo: \[ \log \mbox{fertility}_{i} = \beta_{0} + \beta_{1}\log \mbox{ppgdp}_{i} + \beta_{2}\mbox{pctUrban}_{i} + \varepsilon_{i}, \] donde \(\varepsilon_{i}\sim N(0,\sigma^{2})\) y \(cov(\varepsilon_{j},\varepsilon_{k})=0\).

La Figura 4.8 muestra el gráfico de los residuos para este ajuste. Aquí vemos que los problemas de no linealidad y heterocedasticidad se corrigieron al realizar la transformación logarítmica.

mod.UN11.trans = lm(log(fertility)~log(ppgdp)+pctUrban,data = UN11)
res.UN11.trans = studres(mod.UN11.trans)
par(mfrow=c(1,2))
plot(mod.UN11.trans$fitted.values,res.UN11.trans,xlab='valores ajustados',
     ylab='residuos estudentizados')
lines(lowess(res.UN11.trans~mod.UN11.trans$fitted.values),col=2)
abline(h=0,lty=2)
plot(mod.UN11.trans$fitted.values,abs(res.UN11.trans),xlab='valores ajustados',
     ylab='| residuos estudentizados |')
lines(lowess(abs(res.UN11.trans)~mod.UN11.trans$fitted.values),col=2)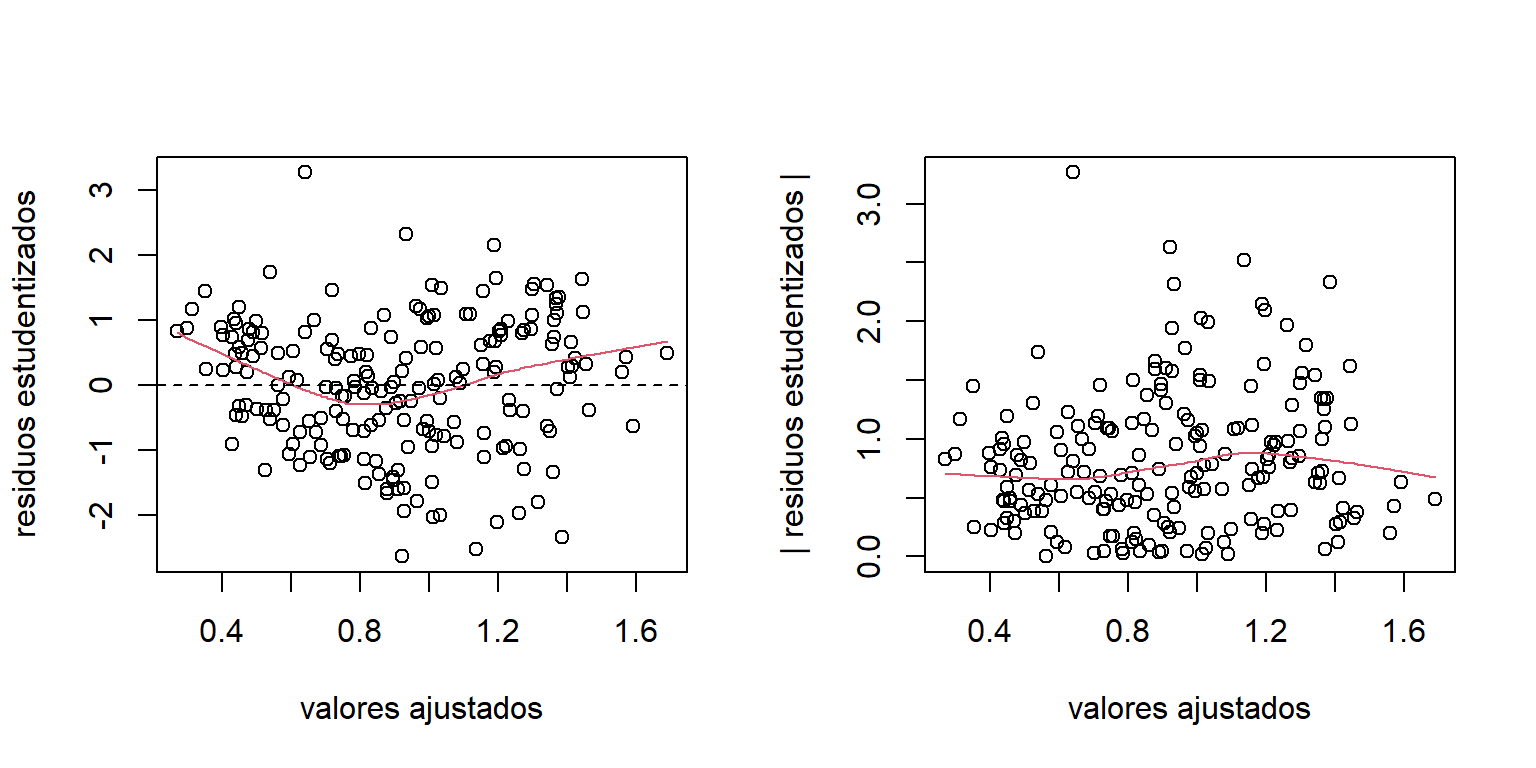
Datos de la ONU. Gráficos de los residuos para el modelo transformado.

Figure 4.8: Datos de la ONU. Gráficos de los residuos para el modelo transformado.

4.2 Método de Box-Cox

Para la corrección del supuesto de normalidad y varianza constante, es posible implementar transformaciones en potencia para la variable respuesta. Esto es, \(y^{*}=y^{\lambda}\). Dado que el valor de \(\lambda\) es desconocido, la idea del método de Box-Cox es estimar el modelo lineal para diferentes valores de \(\lambda\) y determinar el valor que proporciona el mejor ajuste. Sin embargo, aquí encontramos dos problemas.

Primero, la transformación en potencia tiene un problema de discontinuidad en \(\lambda=0\). Puesto que cuando \(\lambda\) tiende a cero, \(y^{*}\) se acerca a \(1\). Para resolver esto, se puede utilizar \(y^{*} = (y^{\lambda}-1)/\lambda\). De esta forma, cuando \(\lambda\) tiende a cero, \(y^{*}\) se acerca a \(\log y\). Segundo, cuando \(\lambda\) cambia, los valores \(y^{*}\) varía drásticamente. Esto hace que los modelos ajustados no se puedan comparar fácilmente.

La transformación que permite que los modelos ajustados sean comparables es: \[\begin{equation} y^{(\lambda)} = \begin{cases} \frac{y^{\lambda}-1}{\lambda \dot{y}^{\lambda-1}}, & \mbox{si }\lambda \neq 0, \\ \dot{y}\log y & \mbox{si } \lambda=0, \end{cases} \tag{4.1} \end{equation}\] donde \(\dot{y} = \log \left[1/n \sum_{i=1}^{n}\log y_{i}\right]\) es la media geométrica de la variable respuesta.

Entonces, el método de Box-Cox es el siguiente:

  1. Determinar una secuencia de valores para \(\lambda\), \((\lambda_{1},\lambda_{2},\ldots,\lambda_{K})\). Por lo general, se seleccionan valores en el intervalo \([-2,2]\).
  2. Ajustar el modelo: \[ y_{ij}^{(\lambda_k)} = \beta_{0} + \beta_{1}x_{i1} + \beta_{2}x_{i2} + \ldots + \beta_{p-1}x_{i,p-1} + \varepsilon_{i}, \] para cada valor de \(\lambda_{k}\), \(k=1,\ldots,K\). Al utilizar la transformación (4.1), las sumas de cuadrados para modelos con diferentes valores de \(\lambda\) son comparables.
  3. Seleccionar el modelo que minimiza la suma de cuadrados de los residuos, \(SS_{res}(\lambda)\). Equivalentemente, el \(\lambda\) que maximiza la verosimilitud.
  4. Luego de encontrar el valor de \(\lambda\) óptimo, se ajusta el modelo transformando la variable respuesta \(y^{\lambda}\), si \(\lambda\neq 0\), o \(\log y\) si \(\lambda =0\). Es decir que (@ref{eq:boxcoxtrans}) se utiliza solo en el paso de comparación de modelos ajustados.

Puesto que \(\lambda\) es una variable aleatoria, también se puede hacer una estimación por intervalos de confianza. Para esto primero consideremos la función de log-verosimilitud: \[ \ell(\boldsymbol \beta,\sigma^{2} | \lambda) = -\frac{2}{n}\log \left( 2\pi\sigma^{2}\right) - \frac{1}{2\sigma^{2}}\sum_{i=1}^{n}\left( y_{i}^{\lambda} - \boldsymbol x_{i}'\boldsymbol \beta\right)^{2} = -\frac{2}{n}\log \left( 2\pi\sigma^{2}\right) - \frac{1}{2\sigma^{2}}SS_{res}(\lambda). \] Aquí vemos que el valor de \(\lambda\) que maximiza la verosimilitud es el mismo que minimiza la suma de cuadrados de los residuos.

Un intervalo de confianza se puede construir a partir del siguiente estadístico de prueba: \[ G_{0}^{2} = -2\left[ \ell(\boldsymbol \beta,\sigma^{2} | \lambda=1) - \ell(\boldsymbol \beta,\sigma^{2} | \lambda=\widehat{\lambda}) \right]. \] Si \(\lambda=1\), entonces asintóticamente \(G_{0}^{2} \sim \chi^{2}_{1}\). Por lo tanto, el intervalo del \((1-\alpha)\times 100\)% de confianza para \(\lambda\) está definido por los valores de \(\lambda\) que cumplen con la condición: \[ \ell(\boldsymbol \beta,\sigma^{2} | \lambda) \geq \ell(\boldsymbol \beta,\sigma^{2} | \lambda=\widehat{\lambda}) - \frac{1}{2}\chi^{2}_{1,1-\alpha}. \]

4.2.1 Datos de educación. Transformación de Box-Cox

Dado que el análisis de residuso para el ajuste del modelo para los datos de educación mostró que hay problemas de heterocedasticidad, vamos a encontrar una transformación que resuelva de problema usando el método de Box-Cox. Para esto usamos la función boxcox de la librería MASS:

boxcox.educ = MASS::boxcox(mod.educ,lambda=seq(-3,3,length.out = 1000),
                               ylab='log-verosimilitud')
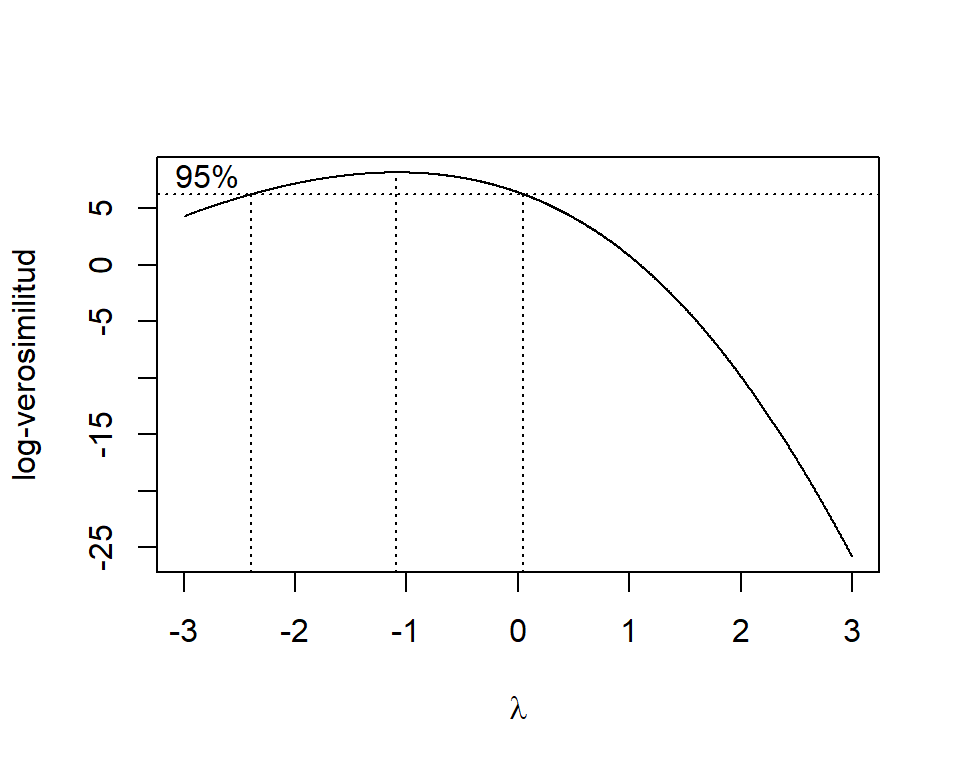
\label{fig:EducBC} Datos de educación. Perfiles de verosimilitud para $\lambda$.

Figure 4.9: Datos de educación. Perfiles de verosimilitud para \(\lambda\). 

boxcox.educ$x[boxcox.educ$y ==max(boxcox.educ$y)] # valor que maximiza la log-verosimilitud
## [1] -1.09009

Estos resultados nos indican que \(\widehat{\lambda}= -1.09\). Por lo cuál, podemos utilizar una transformación inversa \((\lambda=-1)\). Entonces, el modelo propuesto es: \[ 1/y_{i} = \beta_{0} + \beta_{1}\mbox{X1}_{i}+ \beta_{2}\mbox{X2}_{i} + \beta_{3}\mbox{X3}_{i} + \varepsilon_{i}, \] donde \(\varepsilon_{i}\sim N(0,\sigma^{2})\) y \(cov(\varepsilon_{j},\varepsilon_{k})=0\).

Ahora procedemos a hacer el análisis de los residuos del modelo transformado:

mod.educ.trans = lm(1/Y~X1+X2+X3,data=education)
res.educ.trans = studres(mod.educ.trans)
par(mfrow=c(1,2))
plot(mod.educ.trans$fitted.values,res.educ.trans,
     xlab='valores ajustados',ylab='residuos estudentizados')
lines(lowess(res.educ.trans~mod.educ.trans$fitted.values),col=2)
abline(h=0,lty=2)
plot(mod.educ.trans$fitted.values,abs(res.educ.trans),
     xlab='valores ajustados',ylab='| residuos estudentizados |')
lines(lowess(abs(res.educ.trans)~mod.educ.trans$fitted.values),col=2)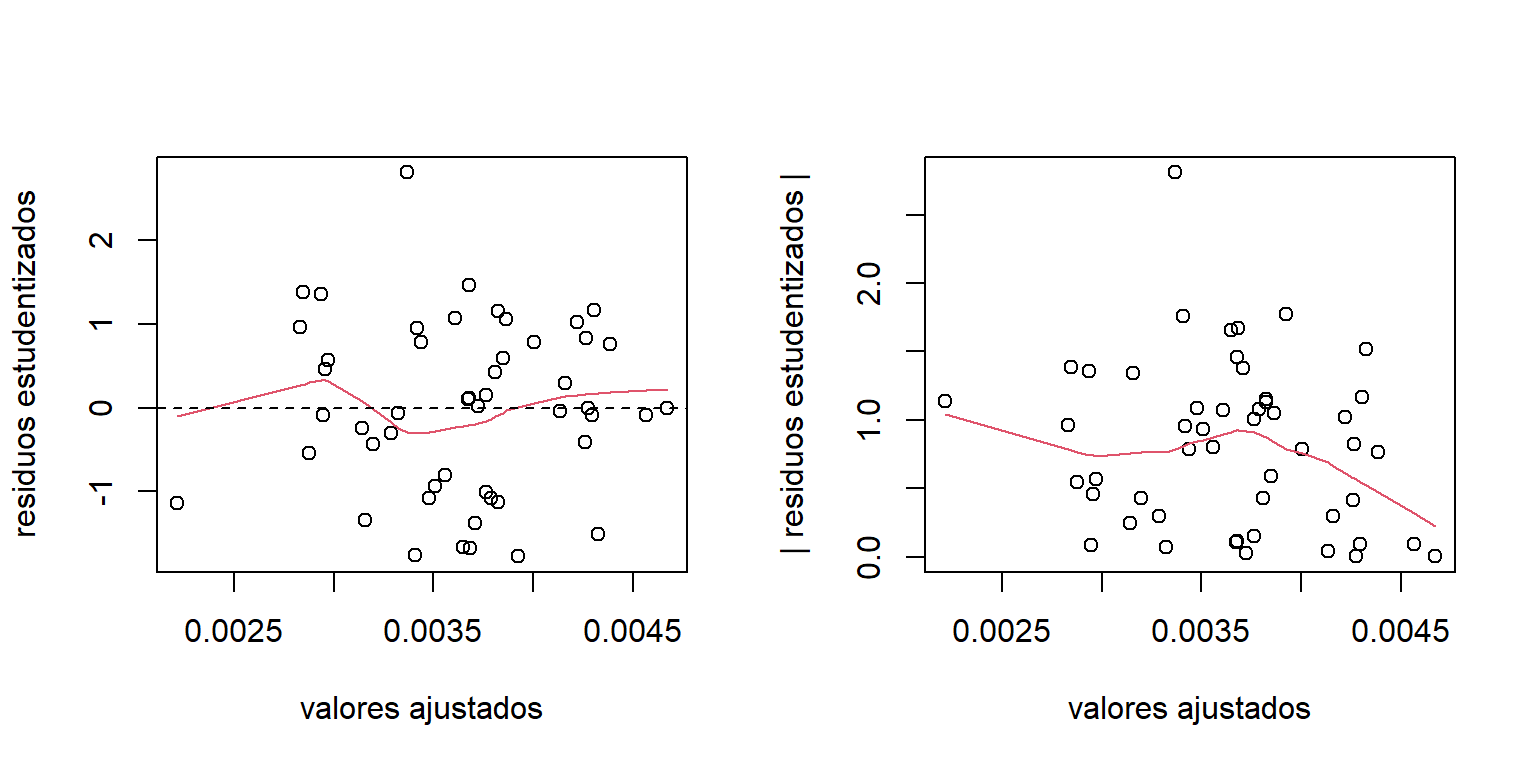
Datos de educación. Graficos de los residuos para el modelo transformado.

Figure 4.10: Datos de educación. Graficos de los residuos para el modelo transformado.

En la Figura 4.10 vemos que la transformación propuesta corrigió el problema de heterocedasticidad. Adicionalmente, por medio de la Figura 4.11 podemos verificar que el supuesto de normalidad se cumple.

car::qqPlot(mod.educ.trans,distribution = 'norm',ylab='residuos estudentizados')
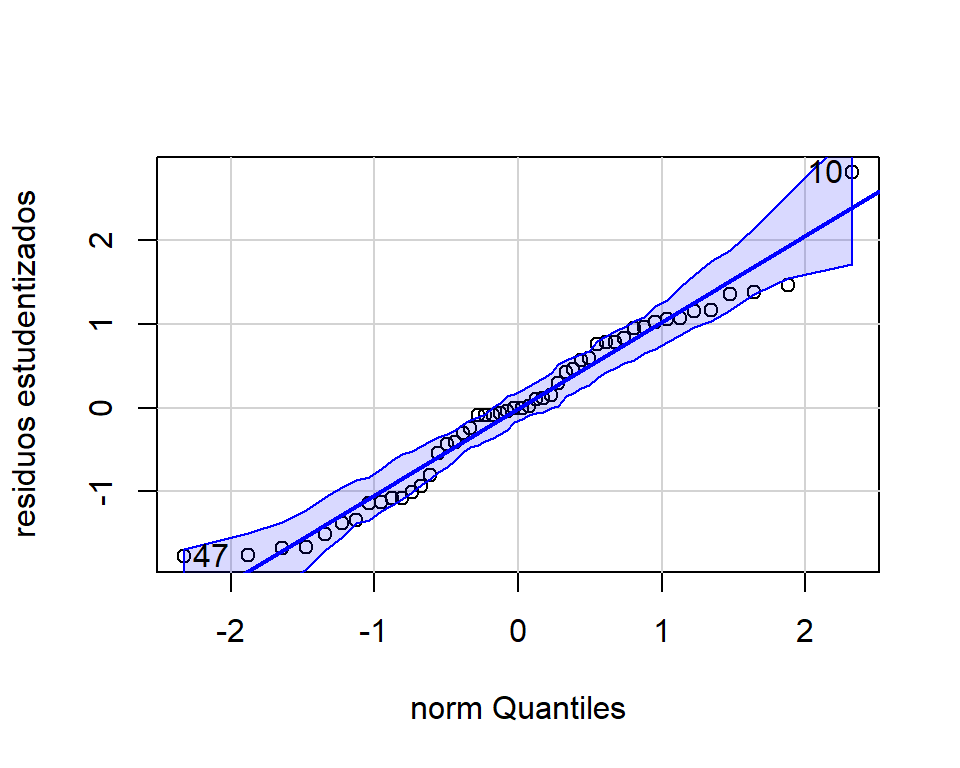
Datos de educación. Graficos de normalidad de los residuos para el modelo transformado.

Figure 4.11: Datos de educación. Graficos de normalidad de los residuos para el modelo transformado. 

## [1] 10 47

Puesto que se cumplen los supuestos del modelo transformado, ahora procedemos a interpretar los resultados.

summary(mod.educ.trans)
## 
## Call:
## lm(formula = 1/Y ~ X1 + X2 + X3, data = education)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -7.609e-04 -3.732e-04 -1.640e-06  3.468e-04  1.158e-03 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.220e-02  1.366e-03   8.934 1.29e-11 ***
## X1          -6.613e-07  5.698e-07  -1.161 0.251816    
## X2          -7.302e-04  1.286e-04  -5.676 8.83e-07 ***
## X3          -1.444e-05  3.489e-06  -4.139 0.000147 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.0004487 on 46 degrees of freedom
## Multiple R-squared:  0.5897, Adjusted R-squared:  0.5629 
## F-statistic: 22.04 on 3 and 46 DF,  p-value: 5.417e-09

A partir de estos resultados podemos concluir que la población en áreas urbanas no tiene un aporte signficativo en el modelo cuando las otras dos covariables ya están incluidas. Mientras que, el ingreso per cápita y la población menor de 18 años tienen un efecto positivo significativo sobre el gasto en educación pública (recordemos que se hizo una transformación inversa).

Puesto que hicimos transformaciones, la interpretación de los coeficientes se hace sobre la variable respuesta transformada.

Ahora, supogamos que queremos hacer la predicción del gasto medio en educación pública para los estados que tengan una población de \(\mbox{X1}=650\), un ingreso per cápita de \(\mbox{X2=4.5}\) y una población menor de 18 años de \(\mbox{X3}=320\). A partir del modelo ajustado tenemos que:

x0.educ = data.frame(X1=650,X2=4.5,X3=320)
pred.educ.trans = predict(mod.educ.trans,x0.educ,interval='confidence') 
1/pred.educ.trans
##        fit      lwr      upr
## 1 258.6228 268.5117 249.4364
Por lo que intervalo del 95% de confianza para el gasto medio en educación pública para los estados con las características expresadas anteriormente es (249.44, 268.51).

4.3 Mínimos cuadrados ponderados

El método de mínimos cuadrados ponderados (MCP) es una alternativa para estimar un modelo lineal en presencia de heterocedasticidad. La idea de esta técnica es calcular las desviaciones entre las observaciones \((y_{i})\) y los valores ajustados \((\widehat{y}_{i})\) usando pesos \((w_{i})\) inversamente proporcionales a la varianza de \(y_{i}\).

Asumamos que el modelo generador de los datos es: \[\begin{equation} \boldsymbol y= \boldsymbol X\boldsymbol \beta+ \boldsymbol \varepsilon, \mbox{ donde }\boldsymbol \varepsilon\sim N(\boldsymbol 0,\sigma^{2}\boldsymbol V), \tag{4.2} \end{equation}\] donde \(\boldsymbol V\) es una matriz diagonal \((n \times n)\): \[ \boldsymbol V= \begin{pmatrix} v_{11} & 0 & 0 & \ldots & 0 \\ 0 & v_{22} & 0 & \ldots & 0 \\ 0 & 0 & v_{33} & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & v_{nn} \end{pmatrix}. \] Esto quiere decir que tenemos presencia de hetorocedasticidad, donde \(V(\varepsilon_{i}) = \sigma^{2}v_{ii}\). Recordemos que si aplicamos el estimador por MCO, las estimaciones siguen siendo insesgadas pero son ineficientes. Además, las varianzas estimadas de \(\widehat{\boldsymbol \beta}\), y de las predicciones, están mal calculadas. Lo que puede afectar la cobertura de los intervalos de confianza y el nivel de signficancia de las pruebas de hipótesis.

La función de verosimilitud del modelo (4.2), asumiendo que \(\boldsymbol V\) es conocida, es: \[ L(\boldsymbol \beta,\sigma^{2} | \boldsymbol V) = \frac{1}{(2\pi)^{n/2}|\sigma^{2}\boldsymbol V|^{1/2}}\exp \left[-\frac{1}{2\sigma^{2}}(\boldsymbol y- \boldsymbol X'\boldsymbol \beta)'\boldsymbol V^{-1}(\boldsymbol y- \boldsymbol X'\boldsymbol \beta) \right]. \] Por lo que para encontrar el estimador de \(\boldsymbol \beta\) debemos minimizar la suma de cuadrados ponderada: \[\begin{equation} SS_{Wres} = (\boldsymbol y- \boldsymbol X'\boldsymbol \beta)'\boldsymbol W(\boldsymbol y- \boldsymbol X'\boldsymbol \beta) = \sum_{i=1}^{n} w_{ii}(y_{i} - \boldsymbol x_{i}'\boldsymbol \beta)^{2}, \tag{4.3} \end{equation}\] donde \(\boldsymbol W= \boldsymbol V^{-1}\), es decir que \(w_{ii}= \frac{1}{v_{ii}}\). Note que las observaciones con mayor varianza tienen menor peso en la estimación de \(\boldsymbol \beta\).

Al minimizar (4.3) se obtiene el estimador por MCP: \[ \widehat{\boldsymbol \beta}_{W} = (\boldsymbol X'\boldsymbol W\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol W\boldsymbol y. \] Además, \[\begin{equation} V(\widehat{\boldsymbol \beta}_{W}) = \sigma^{2}(\boldsymbol X'\boldsymbol W\boldsymbol X)^{-1}. \tag{4.4} \end{equation}\] Si \(\boldsymbol V\) está correctamente especificada, se puede probar que \(\widehat{\boldsymbol \beta}_{W}\) es el mejor estimador insesgado de \(\boldsymbol \beta\).

Los residuos del ajuste del modelo son: \[ e_{Wi} = \sqrt{w_{ii}}(y_{i} - \widehat{y}_{i}), \mbox{ de forma matricial }\boldsymbol e_{W} = \boldsymbol W^{1/2}(\boldsymbol y- \boldsymbol X\widehat{\boldsymbol \beta}_{W}), \] donde \(\boldsymbol W= \boldsymbol W^{1/2}\boldsymbol W^{1/2}\). De este resultado obtenemos el estimador insesgado de \(\sigma^{2}\): \[ \widehat{\sigma}^{2} = \frac{1}{n-p}\sum_{i=1}^{n}w_{ii}(y_{i}-\boldsymbol x_{i}'\widehat{\boldsymbol \beta})^{2} = \frac{1}{n-p}(\boldsymbol y- \boldsymbol X\widehat{\boldsymbol \beta})'\boldsymbol W(\boldsymbol y- \boldsymbol X\widehat{\boldsymbol \beta}). \]

Aqui estamos asumiendo que los pesos \((w_{ii})\) son conocidos. Lo que en la práctica es poco común. Estos pesos pueden ser determinados por conocimiento de los datos, experiencia, o información teórica del modelo. Alternativamente, estos se pueden calcular a partir de los residuos obtenidos por el estimador MCO.

Es común que \(\sigma^{2}_{i}\) varíe de acuerdo a una o varias covariables, o con respecto \(E(y_{i}|\boldsymbol x_{i})\). Por ejemplo, en los datos de educación parece que la varianza incrementa con \(E(y_{i}| \boldsymbol x_{i})\). En este caso podemos aplicar el siguiente procedimiento:

  1. Ajustar el modelo por MCO y analizar los residuos.
  2. Ajustar un modelo para el valor absoluto de los residuos \((|e_{i}|)\), o los residuso al cuadrado \((e^{2}_{i})\), en función de las covariables: \[ |e_{i}| = \gamma_{0} + \gamma_{1}x_{i1}+ \ldots + \gamma_{p-1}x_{i,p-1} + \varepsilon_{ei}. \] De esta ajuste obtenemos una estimación para la desviación estándar \((\sigma_{i})\). Si ajustamos un modelo para los residuos al cuadrado, estamos estimando la varianza \((\sigma^{2})\).
  3. Usar los valores ajustados el modelo anterior para estimar los pesos \((w_{ii})\).

Si \(\widehat{\boldsymbol \beta}_{W}\) difiere mucho de \(\widehat{\boldsymbol \beta}\), es posible repetir el proceso anterior una vez más (mínimos cuadrados iterativamente ponderados).

Dado que estamos estimando los pesos, la varianza de los coeficientes (4.4) es aproximada. Sin embargo, esta aproximación es muy buena si el tamaño de muestra no es muy pequeño.

Datos de educación. Minímos cuadrados ponderados

Retomemos el modelo para los datos de educación. En la Figura @ref{fig:Educres} vemos que hay heterocedasticidad. Particularmente vemos que la variabilidad crece a medida que aumentan los valores ajustados. Ya vimos que por medio de una transformación inversa sobre la variable respuesta se corrige el problema.

El problema de hacer transformaciones es que los coeficientes estimados pierden interpretación. Así que, alternativamente, vamos a implementar el método de minímos cuadrados ponderados. Dado que desconocemos los pesos, vamos a estimarlos usando el procedimiento que se explicó anteriormente.

Primero vamos a ajustar el siguiente modelo para el valor absoluto de los residuos: \[ |e_{i}| = \gamma_{0} + \gamma_{1}\mbox{X1}_{i}+ \gamma_{2}\mbox{X2}_{i} + \gamma_{3}\mbox{X3}_{i} + \varepsilon_{ei}. \]

mod.stdev.educ = lm(abs(res.educ)~X1+X2+X3,data = education)
summary(mod.stdev.educ)
## 
## Call:
## lm(formula = abs(res.educ) ~ X1 + X2 + X3, data = education)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.23416 -0.38164 -0.00938  0.32668  1.37892 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -4.6137734  1.7454477  -2.643   0.0112 *  
## X1          -0.0014511  0.0007281  -1.993   0.0522 .  
## X2           0.7274821  0.1643850   4.425 5.87e-05 ***
## X3           0.0092325  0.0044583   2.071   0.0440 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5734 on 46 degrees of freedom
## Multiple R-squared:  0.3199, Adjusted R-squared:  0.2756 
## F-statistic: 7.214 on 3 and 46 DF,  p-value: 0.0004565

Por lo tanto, las estimaciones de las desviaciones estándar de los errores son: \[ \widetilde{\sigma}_{i} = s_{i} = -4.614 -0.001\mbox{X1}_{i} + 0.727\mbox{X2}_{i} + 0.009\mbox{X3}_{i}. \] De este ajuste obtenemos los pesos \(w_{ii} = \frac{1}{s_{i}^{2}}\), y luego, estimamos el modelo por MCP:

w = 1/mod.stdev.educ$fitted.values^2
mod.educ.mcp = lm(Y~X1+X2+X3,data=education,weights = w)
summary(mod.educ.mcp)
## 
## Call:
## lm(formula = Y ~ X1 + X2 + X3, data = education, weights = w)
## 
## Weighted Residuals:
##     Min      1Q  Median      3Q     Max 
## -93.670 -32.522  -9.149  31.582  86.742 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -404.85597   84.79548  -4.774 1.87e-05 ***
## X1             0.05062    0.03778   1.340    0.187    
## X2            62.43586   10.29479   6.065 2.32e-07 ***
## X3             1.11736    0.20099   5.559 1.32e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 44.98 on 46 degrees of freedom
## Multiple R-squared:  0.6528, Adjusted R-squared:  0.6302 
## F-statistic: 28.83 on 3 and 46 DF,  p-value: 1.219e-10

La Figura 4.12 muestra los gráficos de los residuos ponderados. Aquí podemos observar que los residuos ponderados no muestra heterocedasticidad.

res.educ.mcp = mod.educ.mcp$residuals*sqrt(w)
par(mfrow=c(1,2))
plot(mod.educ.mcp$fitted.values,res.educ.mcp,
     xlab='valores ajustados',ylab='residuos ponderados')
lines(lowess(res.educ.mcp~mod.educ.mcp$fitted.values),col=2)
abline(h=0,lty=2)
plot(mod.educ.mcp$fitted.values,abs(res.educ.mcp),
     xlab='valores ajustados',ylab='| residuos ponderados |')
lines(lowess(abs(res.educ.mcp)~mod.educ.mcp$fitted.values),col=2)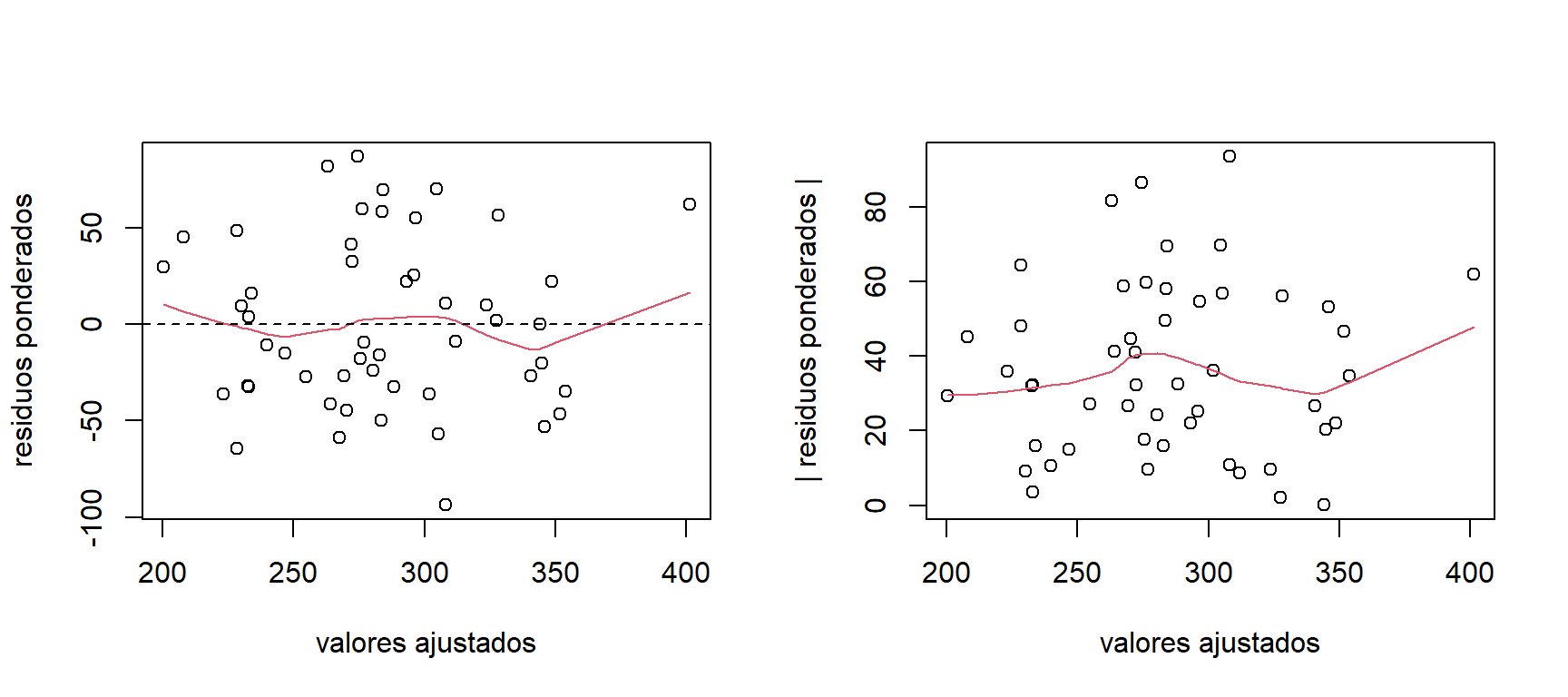
Datos de educación. Graficos de los residuos ponderados.

Figure 4.12: Datos de educación. Graficos de los residuos ponderados.

El ajuste por mínimos cuadrados ponderados es:

summary(mod.educ.mcp)
## 
## Call:
## lm(formula = Y ~ X1 + X2 + X3, data = education, weights = w)
## 
## Weighted Residuals:
##     Min      1Q  Median      3Q     Max 
## -93.670 -32.522  -9.149  31.582  86.742 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -404.85597   84.79548  -4.774 1.87e-05 ***
## X1             0.05062    0.03778   1.340    0.187    
## X2            62.43586   10.29479   6.065 2.32e-07 ***
## X3             1.11736    0.20099   5.559 1.32e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 44.98 on 46 degrees of freedom
## Multiple R-squared:  0.6528, Adjusted R-squared:  0.6302 
## F-statistic: 28.83 on 3 and 46 DF,  p-value: 1.219e-10

Aquí llegamos a conclusiones similares a las obtenidas por medio del modelo transformado. El efecto de la población en áreas urbanas no es significativo. Las otras dos covariables si aportan significativamente al modelo. En este caso, dado que no aplicamos transformaciones, los coeficientes si tienen interpretación. Por ejemplo de la estimación de \(\beta_{3}\) podemos concluir que: el gasto per cápita medio en educación pública aumenta en 1.117 USD por cada 1000 personas menores de 18 años.

Ahora, hagamos la predicción del gasto medio en educación pública para las características: \(\mbox{X1}=650\), \(\mbox{X2=4.5}\) y \(\mbox{X3}=320\):

predict(mod.educ.mcp,x0.educ,interval='confidence')
##        fit      lwr      upr
## 1 266.5599 257.8442 275.2755

Por medio del estimador de MCP obtenemos el siguiente intervalo del 95% de confianza: (257.844, 275.275). Este intervalo es parecido al calculado usando el modelo transformado, aunque tiene una longitud un poco más pequeña.

References

Behar, Roberto. 2002. Validación de Supuestos En El Modelo de Regresión.