Capítulo 3 Evaluación de los supuestos del modelo

Ejemplo 1. Datos de peso al nacer

Retomemos la base de datos de bajo peso al nacer (disponible en el campus virtual), y consideremos el siguiente modelo: \[ \mbox{weight}_{i} = \beta_{0} + \beta_{1}\mbox{age}_{i} + \beta_{2}\mbox{motherage}_{i} + \beta_{3}\mbox{mnocig}_{i} + \beta_{4}\mbox{mppwt}_{i} + \varepsilon_{i}, \] con \(\varepsilon_{i} \sim N\left(0,\sigma^{2} \right)\) y \(cov(\varepsilon_{j},\varepsilon_{k})=0\), para todo \(j \neq k\).

El ajuste del modelo es:

Birthweight = read.csv('birthweight.csv')
mod.birthweight = lm(weight ~ age + motherage + mnocig + mppwt, data=Birthweight)
summary(mod.birthweight)

## 
## Call:
## lm(formula = weight ~ age + motherage + mnocig + mppwt, data = Birthweight)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.78765 -0.35948  0.09209  0.35024  0.75018 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -4.104029   1.011723  -4.056 0.000247 ***
## age          0.168027   0.024916   6.744 6.24e-08 ***
## motherage    0.001751   0.012335   0.142 0.887900    
## mnocig      -0.014417   0.005421  -2.660 0.011493 *  
## mppwt        0.014838   0.009530   1.557 0.127966    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4073 on 37 degrees of freedom
## Multiple R-squared:  0.627,  Adjusted R-squared:  0.5867 
## F-statistic: 15.55 on 4 and 37 DF,  p-value: 1.5e-07

La edad gestacional y el número de cigarrillos consumidos por la madre tienen efectos signficativos sobre el peso del recién nacido. El primero es un factor de protección, a mayor edad gestacional mayor será el peso del bebé. Mientras que, el consumo de cigarrillos es un factor de riesgo. A mayor consumo, menor peso tendrá el recién nacido. La edad y el peso de la madre, aunque tienen efectos positivos, no son covariables significativas cuando las otras dos covariables ya están incluidas en el modelo.

Ejemplo 2. Ventas de helados

La base de datos icecream (del paquete orcutt de R) recopila la siguiente información tomada cada cuatro semanas durante dos años (marzo 1951 a julio 1953):

• price: precio promedio del helado (dolares por bote)
• cons: consumo medio de helado (botes por persona)
• temp: temperatura promedio (en Fahrenheit)

La Figura @ref{fig:icecream} muestra la relación entre las variables. Aquí podemos observar que a mayor temperatura, el consumo de helado se incrementa. Por otro lado, la relación con el precio no es tan fuerte.

library(orcutt)
data("icecream")
pairs(icecream[,c(2,1,4)])

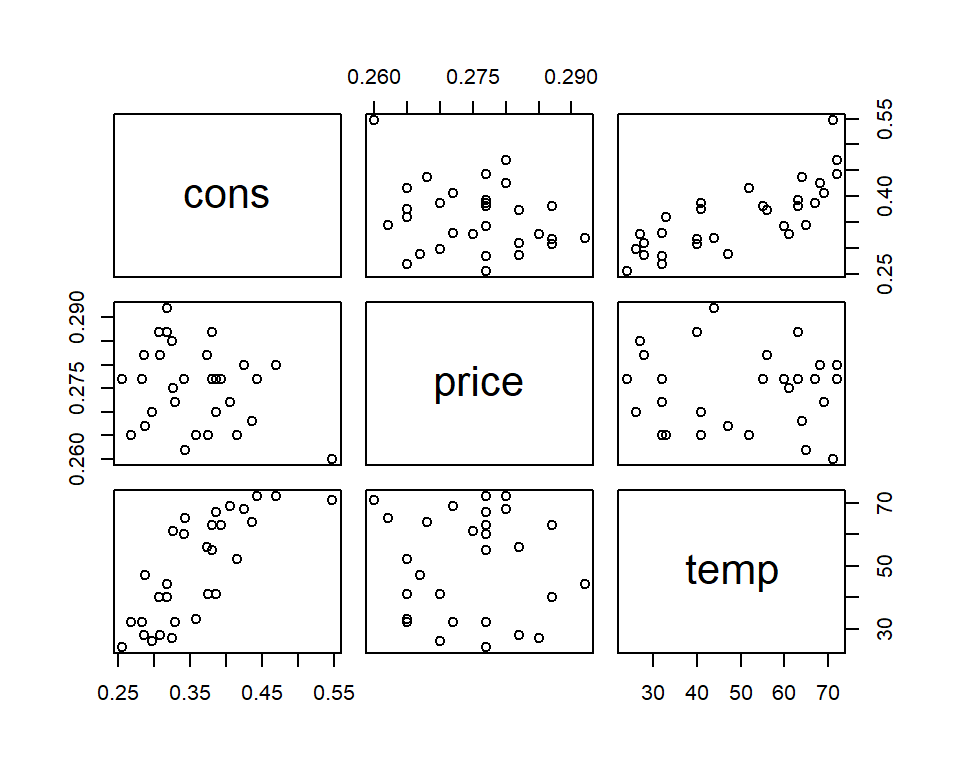
Figure 3.1: Relación entre las variables de los datos de ventas de helados.

El objetivo del estudio es explicar el consumo de helado en función del precio y la temperatura. Para esto se propone el siguiente modelo: \[ \mbox{cons}_{i} = \beta_{0} + \beta_{1}\mbox{price}_{i} + \beta_{2}\mbox{temp}_{i} + \varepsilon_{i}, \] con \(\varepsilon_{i} \sim N\left(0,\sigma^{2} \right)\) y \(cov(\varepsilon_{j},\varepsilon_{k})=0\), para todo \(j \neq k\).

El resumen del modelo es el siguiente:

  mod.icecream = lm(cons~price+temp,data=icecream)
summary(mod.icecream)

## 
## Call:
## lm(formula = cons ~ price + temp, data = icecream)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.08226 -0.02051  0.00184  0.02272  0.10076 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.59655    0.25831   2.309   0.0288 *  
## price       -1.40176    0.92509  -1.515   0.1413    
## temp         0.00303    0.00047   6.448 6.56e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.04132 on 27 degrees of freedom
## Multiple R-squared:  0.6328, Adjusted R-squared:  0.6056 
## F-statistic: 23.27 on 2 and 27 DF,  p-value: 1.336e-06

De aquí podemos concluir que alrededor del 70% de la variabilidad del consumo de helado está explicado por el modelo propuesto. Además, el efecto de la temperatura sobre el consumo de helado es signficativamente positivo. Aunque la relación con el precio es negativa, esta no es significativa.

Ejemplo 3. Longitud del pez lobina boca chica

La base de datos wblake (de la librería alr4) contiene la edad (en años) y longitud (en mm) de 439 peces lobina boca chica del lago West Bearskin en el nordeste de Minnesota en 1999. El objetivo del estudio es determinar los patrones de crecimiento de este tipo de pez.

library(alr4)
data("wblake")
plot(Length~Age,data=wblake,xlab='edad (años)',ylab='longitud (mm)')

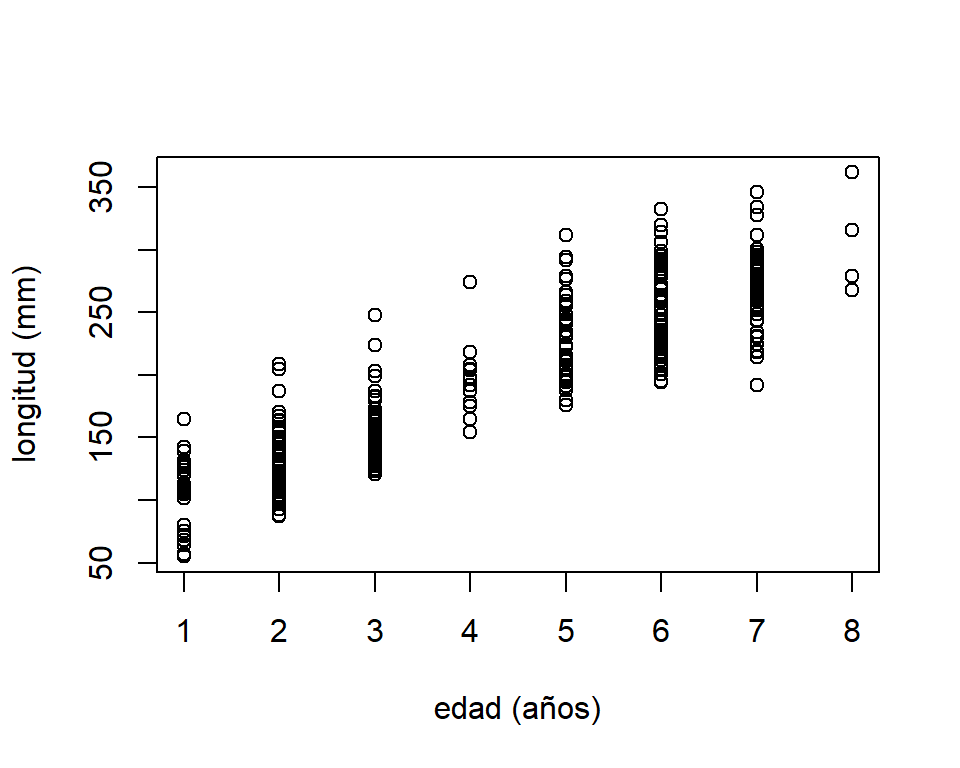
Figure 3.2: Relación entre la edad y la longitud de los peces lobina boca chica.

La Figura @ref{fig:bassFig} muestra que la relación entre estas dos variables se puede aproximar a una recta, por lo cuál se propone el siguiente modelo: \[ \mbox{length}_{i} = \beta_{0} + \beta_{1}\mbox{age}_{i} + \varepsilon_{i} \] con \(\varepsilon_{i} \sim N\left(0,\sigma^{2} \right)\) y \(cov(\varepsilon_{j},\varepsilon_{k})=0\), para todo \(j \neq k\).

El resumen del ajuste es el siguiente:

mod.bass = lm(Length~Age,data=wblake)
summary(mod.bass)

## 
## Call:
## lm(formula = Length ~ Age, data = wblake)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -85.794 -19.499  -4.499  16.177  94.853 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  65.5272     3.1974   20.49   <2e-16 ***
## Age          30.3239     0.6877   44.09   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 28.65 on 437 degrees of freedom
## Multiple R-squared:  0.8165, Adjusted R-squared:  0.8161 
## F-statistic:  1944 on 1 and 437 DF,  p-value: < 2.2e-16

Estos resultados muestran que la edad del pez tiene un efecto significativamente positivo. Por cada año del pez, la longitud aumenta 30 milimetros en promedio. Adicionalmente, esta covariable explica el 81% de la variabilidad de la longitud.

La validez de las conclusiones hechas en estos ejemplos descansa en el cumplimiento de los supuestos sobre los errores. Por esta razón, es de gran importancia que tengamos herramientas para evaluar si los datos analizados no muestran ningún alejamiento de los supuestos asumidos.

3.1 Supuestos del modelo linea múltiple

En el modelo de regresión lineal múltiple: \[ y_{i}=\beta_{0} + \beta_{1} x_{i1}+\beta_{2} x_{i2}+\ldots + \beta_{p-1} x_{i,p-1} +\varepsilon_{i}, \] asumimos que la relación entre la variable respuesta y las covariables es lineal, al menos de forma aproximada. Además,

1. \(E(\varepsilon_{i})=0\), para \(i=1,\ldots,n\),
2. \(Var(\varepsilon_{i})=\sigma^{2}\). Homogeneidad de varianza en los errores,
3. \(Cov(\varepsilon_{i},\varepsilon_{j})=0\) para todo \(i\neq j\). Los errores están incorrelacionados,
4. \(\varepsilon_{i} \sim Normal(0, \sigma^{2})\). Los errores se distribuyen de forma normal.

La importancia de realizar procedimientos para validar los supuestos, radica en que ellos inciden en las cualidades de los estimadores por MCO. En caso de no cumplirse se pueden perder propiedades importantes. Si no se cumple el supuesto (a) se obtienen estimaciones sesgadas. Si no se cumplen (b) y (c) los estimadores MCO pierden la condición de optimalidad. Si no se cumple (d) se pierde eficiencia e imposibilita la aplicación de inferencias basadas en normalidad.

En general, no se puede detectar una violación a los supuestos a partir de estadísticos del ajuste del modelo (\(R^2\), \(F_0\), valores-\(t\), etc). El diagnostico se puede hacer por métodos gráficos y pruebas formales (pruebas de hipótesis). Ambos métodos son complementarios, los gráficos sugieren formas particulares de incumplimiento del supuesto, mientras las pruebas formales evalúan su importancia (Behar 2002).

3.2 Efectos del incumplimiento de los supuestos

3.2.1 Sesgo por omisión de variables relevantes

Si \(E(\boldsymbol \varepsilon) = \boldsymbol 0\), entonces \(E(\boldsymbol y| \boldsymbol X) = \boldsymbol X\boldsymbol \beta\), y el estimador por MCO es insesgado. Sin embargo, si omitimos variables relevantes dentro del modelo las estimaciones serán sesgadas. Para ver esto, supongamos que el modelo generador de los datos es: \[ \boldsymbol y= \boldsymbol X\boldsymbol \beta+ \boldsymbol \varepsilon= \boldsymbol X_{1}\boldsymbol \beta_{1} + \boldsymbol X_{2}\boldsymbol \beta_{2} + \boldsymbol \varepsilon, \] donde las columnas de la matriz \(n\times p\) de covariables \(\boldsymbol X\) está divida en dos submatrices \(\boldsymbol X_{1}\) y \(\boldsymbol X_{2}\) de dimensiones \(n \times (p-r)\) y \(n\times r\), respectivamente. Además, asumimos que \(\boldsymbol \varepsilon\sim N(\boldsymbol 0, \sigma^{2}\boldsymbol I_{n})\).

Ahora, consideramos estimar el siguiente modelo: \[ \boldsymbol y= \boldsymbol X_{1}\boldsymbol \beta_{1} + \boldsymbol \varepsilon^{*}, \] es decir estamos omitiendo las covariables contenidas en \(\boldsymbol X_{2}\). El estimador de \(\boldsymbol \beta_{1}\) es: \[ \widehat{\boldsymbol \beta}_{1} = (\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'\boldsymbol y, \] y el estimador de \(\sigma^{2}\) es: \[ \widehat{\sigma}^{2}_{1} = \frac{\boldsymbol y'(\boldsymbol I_{n} - \boldsymbol H_{1})\boldsymbol y}{n-(p-r)}, \mbox{ donde }\boldsymbol H_{1} = \boldsymbol X_{1}(\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'. \] El valor esperado de \(\widehat{\boldsymbol \beta}_{1}\) es: \[\begin{equation} \begin{split} E(\widehat{\boldsymbol \beta}_{1}) &= E\left[(\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'\boldsymbol y\right] = (\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'E(\boldsymbol y) \\ &= (\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'E(\boldsymbol X_{1}\boldsymbol \beta_{1} + \boldsymbol X_{2}\boldsymbol \beta_{2} + \boldsymbol \varepsilon) = \boldsymbol \beta_{1} + (\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'\boldsymbol X_{2}\boldsymbol \beta_{2}. \end{split} \nonumber \end{equation}\] Evidentemente, el sesgo de \(\widehat{\boldsymbol \beta}_{1}\) depende de la magnitud de \(\boldsymbol \beta_{2}\). Entre más importante sean los efectos asociados a las covariables omitidas \((\boldsymbol \beta_{2})\), mayor será el sesgo. Si las columnas de \(\boldsymbol X_{1}\) son ortogonales de las columnas de \(\boldsymbol X_{2}\), tenemos que \(\boldsymbol X_{1}'\boldsymbol X_{2} = \boldsymbol 0\). Así que, en este caso particular, \(\widehat{\boldsymbol \beta}_{1}\) es insesgado (así omitamos las covariables en \(\boldsymbol X_{2}\)).

El valor esperado de \(\widehat{\sigma}^{2}_{1}\) es: \[ E(\widehat{\sigma}^{2}_{1}) = \sigma^{2} + \frac{\boldsymbol \beta_{2}'\boldsymbol X'_{2}(\boldsymbol I_{n} - \boldsymbol H_{1})\boldsymbol X_{2}\boldsymbol \beta_{2}}{n-(p-r)}. \] Dado que \((\boldsymbol I- \boldsymbol H_{1})\) es idempotente y, por lo tanto, positiva semi-definida, entonces \(E(\widehat{\sigma}_{1}^{2}) > \sigma^{2}\). Lo que quiere decir que \(\widehat{\sigma}^{2}_{1}\) es un estimador sesgado de \(\sigma^{2}\).

Ahora veamos el efecto de omitir covariables relevantes sobre las predicciones de \(y\) en el punto \(\boldsymbol x_{0} = (\boldsymbol x_{01}', \boldsymbol x_{02}')'\). Tenemos que: \[ \widehat{\boldsymbol y}_{0} = \boldsymbol x_{01}'\widehat{\boldsymbol \beta}_{1} = \boldsymbol x_{01}'(\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'\boldsymbol y. \] El valor esperado de \(\widehat{\boldsymbol y}_{0}\) es: \[ E(\widehat{\boldsymbol y}_{0}) = \boldsymbol x_{01}'E(\widehat{\boldsymbol \beta}_{1}) = \boldsymbol x_{01}'\left[ \boldsymbol \beta_{1} + (\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'\boldsymbol X_{2}\boldsymbol \beta_{2} \right]. \] Por lo tanto las predicciones también son sesgadas, \(E(\widehat{\boldsymbol y}_{0}) \neq \boldsymbol x_{01}'\boldsymbol \beta_{1} + \boldsymbol x_{02}'\boldsymbol \beta_{2}\).

3.2.2 Incorrecta matriz de varianzas de los errores

Cuando \(V(\boldsymbol \varepsilon) = \sigma^{2}\boldsymbol V\), pero asumimos erroneamente que \(V(\boldsymbol \varepsilon) = \sigma^{2}\boldsymbol I_{n}\), el estimador \(\widehat{\boldsymbol \beta}\) sigue siendo insesgado. Pero, tenemos que: \[\begin{equation} \begin{split} V(\widehat{\boldsymbol \beta}) &= V\left[ (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y\right] = (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'V(\boldsymbol y)\boldsymbol X(\boldsymbol X'\boldsymbol X)^{-1} \\ &= \sigma^{2}(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol V\boldsymbol X(\boldsymbol X'\boldsymbol X)^{-1}, \end{split} \nonumber \end{equation}\] es, generalmente, diferente de \(\sigma^{2}(\boldsymbol X'\boldsymbol X)^{-1}\) (la varianza que asumimos como cierta). Igualmente, el estimador por MCO pierde su condición de optimalidad. Es decir, deja de ser el mejor estimador lineal insesgado.

El estimador de \(\sigma^{2}\) es sesgado: \[ E(\widehat{\sigma}^{2}) = \frac{\sigma^{2}}{n-p}E\left[\boldsymbol y'(\boldsymbol I_{n} - \boldsymbol H)\boldsymbol y\right] = \frac{\sigma^{2}}{n-p} \mbox{tr}\left[ \boldsymbol V(\boldsymbol I_{n}-\boldsymbol H)\right]. \] Las predicciones son insesgadas, pero: \[ V(\widehat{y}_{0}) = V(\boldsymbol x_{0}'\widehat{\boldsymbol \beta}) = \sigma^{2}\boldsymbol x_{0}'(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol V\boldsymbol X(\boldsymbol X'\boldsymbol X)^{-1} \boldsymbol x_{0}, \] que es diferente de \(\sigma^{2}\boldsymbol x_{0}'(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol x_{0}\) (la varianza que asumimos como cierta).

Cuando \(\boldsymbol V\) es una matriz diagonal: \[ \boldsymbol V= \begin{pmatrix} v_{11} & 0 & 0 & \ldots & 0 \\ 0 & v_{22} & 0 & \ldots & 0 \\ 0 & 0 & v_{33} & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & v_{nn} \end{pmatrix}, \] tenemos que hay heterocedasticidad. Cada error tiene una varianza diferente \(V(\varepsilon_{j})=\sigma^{2}v_{jj}\), pero están incorrelacionados. Si los valores fuera de la diagonal de \(\boldsymbol V\) son diferentes de cero, entonces los errores están correlacionados.

La correlación de los errores puede esperarse en algunas situaciones. Por ejemplo, si las observaciones son tomadas en el tiempo puede presentarse correlación temporal. En situaciones en las que se pueda garantizar que las observaciones \((y_{1},y_{2},\ldots,y_{n})\) constituyen una muestra aleatoria, no existirá correlación entre los errores, es decir, que es posible controlar este aspecto, algunas ocasiones, controlando el procedimiento de selección de la muestra.

3.2.3 Distribución no normal de los errores

La normalidad de los errores permite la estimación por intervalos de confianza no sólo para los coeficientes de regresión, sino también para la predicción. Igualmente, permite el planteamiento de pruebas de hipótesis sobre los parámetros del modelo. Cuando los errores no son normales, estas inferencias no son exactas y pueden llegar a ser inválidas.

Sin embargo, el teorema central del límite asegura que, bajo ciertas condiciones muy amplias, la inferencias basadas en el estimador de mínimos cuadrados son aproximadamente válidas si el tamaño de muestra es suficientemente grande. Esto significa que los niveles de las pruebas y cobertura de los intervalos de confianza son aproximadamente correctos.

De la misma forma, los efectos negativos de la no normalidad dependen de que tan alejados estamos de la normalidad. Si la distribución de los errores es parecida a la normal (por ejemplo, \(t\)-Student), los efectos negativos no son considerables.

3.3 Residuos del modelo

Los residuos están definidos como: \[ e_{i} = y_{i}- \widehat{y}_{i}, \mbox{ en forma matricial }\boldsymbol e= \boldsymbol y- \widehat{\boldsymbol y}= (\boldsymbol I_{n} - \boldsymbol H)\boldsymbol y. \] Los residuos representan las desviaciones entre las observaciones y el ajuste. Además, estos son combinaciones lineales de los errores: \[ \boldsymbol e= (\boldsymbol I_{n} - \boldsymbol H)(\boldsymbol X\boldsymbol \beta+\boldsymbol \varepsilon) = (\boldsymbol I_{n} - \boldsymbol H)\boldsymbol \varepsilon. \] Por lo tanto toda desviación de las premisas de los errores se debe reflejar en los residuales. Si \(\boldsymbol \varepsilon\sim N(\boldsymbol 0,\sigma^{2}\boldsymbol I_{n})\), entonces: \[ \boldsymbol e\sim N \left[ \boldsymbol 0, \sigma^{2}(\boldsymbol I_{n} - \boldsymbol H) \right]. \] De aquí tenemos que \(V(e_{i}) = (1-h_{ii})\sigma^{2}\) y \(Cov(e_{i},e_{j}) = - h_{ij}\sigma^{2}\), para todo \(i \neq j\). Lo que indica que, aún cuando los errores sean homogéneos en varianza e incorrelacionados, no implica que los residuos lo sean también. Note que los residuos asociados a puntos alejados del centro de los datos tienen menor varianza. Lo que hace difícil detectar violaciones.

Cuando \(n\) es grande comparado con el número de parámetros en el modelo, los residuos si reflejan a los errores en cuanto al comportamiento de su varianza y correlación. Esto es porque \(|h_{ij}| \leq 1\), \(\sum_{i=1}^{n}h_{ii} = n-p\), y \(\sum_{i=1}^{n}h_{ij}=\sum_{j=1}^{n}h_{ij}=1\). Por lo tanto, cuando \(n\rightarrow \infty\), \(V(e_{i}) = \sigma^{2}\) y \(Cov(e_{i},e_{j}) = 0\).

3.3.1 Residuos estudentizados

Para evitar el inconveniente de la varianza no constante de los residuos, es preferible utilizar los residuos estudentizados: \[ r_{i} = \frac{e_{i}}{\sqrt{\hat{\sigma}^{2}(1-h_{ii})}}, \qquad i=1,2,\ldots,n. \] Entonces, \(r_{i}\) tiene varianza constante (\(V(r_{i})=1\)) independiente del lugar de \(\boldsymbol x_{i}\).

3.3.2 Residuos PRESS y R-student

Como veremos más adelante, los residuos estudentizados se pueden utilizar detectar puntos atípicos. El problema es que si la \(i\)-ésima observación es bastante inusual, el ajuste del modelo puede estar muy influenciado por esta observación. Lo que puede producir un residuo pequeño. Por esta razón, también se pueden calcular los residuos de predicción (PRESS). Estos se calculan de la siguiente forma: \[ e_{(i)} = y_{i} - \widehat{y}_{(i)}, \mbox{ para }i=1,\ldots,n, \] donde \(\widehat{y}_{(i)}\) es el valor ajustado para la \(i\)-ésima observación usando todas las observaciones excepto la \(i\)-ésima. Esto implicaría que para calcular los residuos PRESS es necesario ajustar \(n\) veces el modelo. Sin embargo, esto no es así, ya que se puede demostrar que: \[ e_{(i)} = \frac{e_{i}}{1-h_{ii}}. \] La varianza de los residuos PRESS es: \[ V(e_{(i)}) = V\left( \frac{e_{i}}{1-h_{ii}} \right) = \frac{1}{(1-h_{ii})^{2}}V(e_{i}) = \frac{1}{(1-h_{ii})^{2}} [\sigma^{2}(1-h_{ii})] = \frac{\sigma^{2}}{(1-h_{ii})}. \] Si estudentizamos los residuos PRESS obtenemos los residuos R-Student: \[ t_{i} = \frac{e_{i}}{\sqrt{\widehat{\sigma}^{2}_{(i)}(1-h_{ii})}}, \] donde \(\widehat{\sigma}^{2}_{(i)}\) es la estimación de \(\sigma\) usando todas las observaciones excepto la \(i\)-ésima. Se puede demostrar que: \[ \widehat{\sigma}^{2}_{(i)} = \frac{(n-p)\widehat{\sigma}^{2} - e^{2}_{i}/(1-h_{ii})}{n-p-1}. \]

3.4 Evaluación del cumplimiento de los supuestos

En esta sección mostramos la evaluación de los supuestos a través del análisis de los residuos del ajuste (ya sean los residuos estudentizados o los R-Student) usando gráficos y pruebas de hipótesis.

3.4.1 Gráficos de residuos

Un gráfico de los residuos es una forma efectiva de investigar posibles alejamientos de los supuestos. Generalmente, se grafican los residuos estudentizados \((r_{i})\) contra los valores ajustados \(\widehat{y}_{i}\) (o contra alguna de las covariables \(x_{ij}\)). Este tipo de gráfico es de gran ayuda para detectar la correcta especificación del modelo y homocedasticidad. Algunos patrones de residuos se pueden observar en la Figura 3.3.

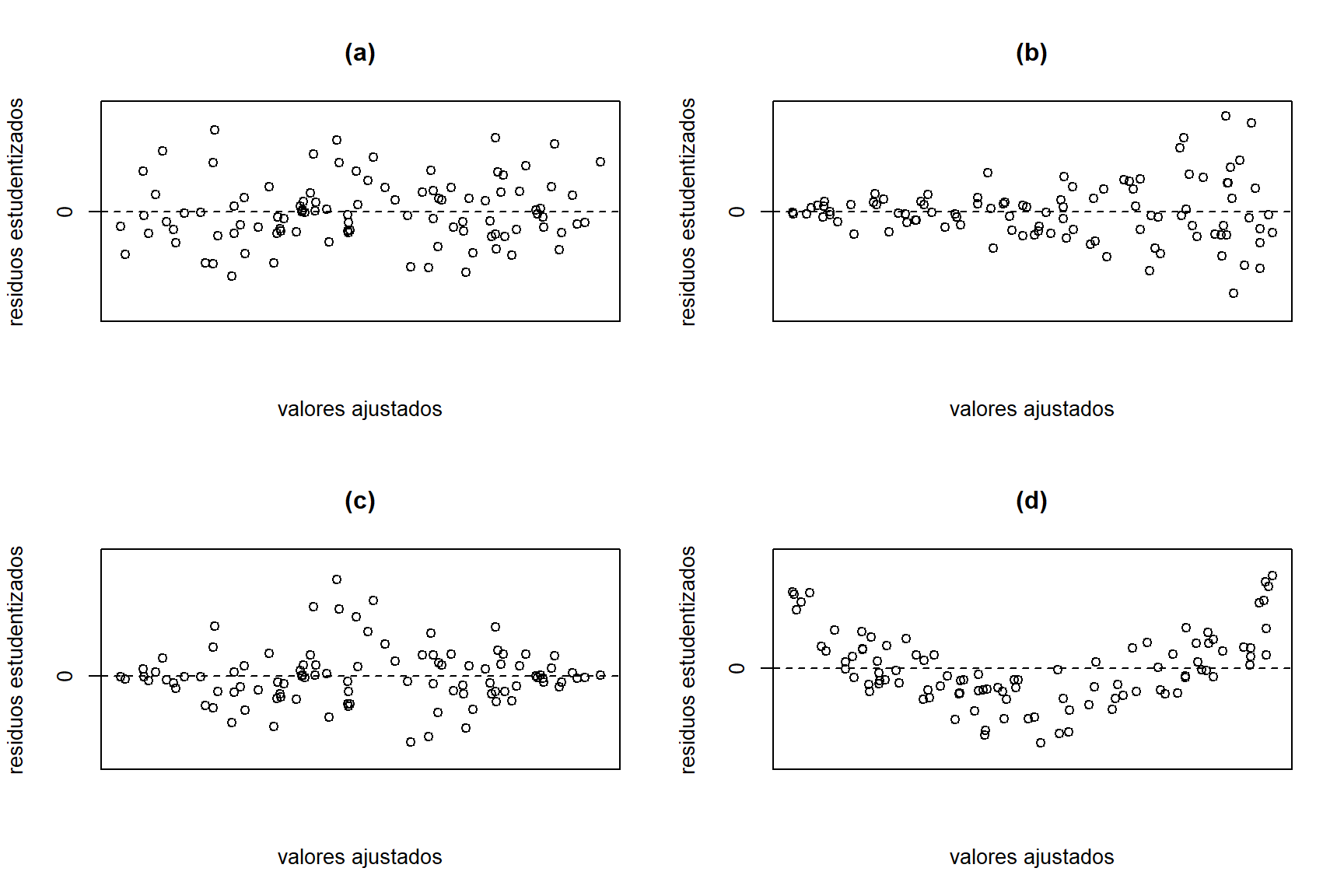
Figure 3.3: Ejemplos de posibles patrones de residuos

La Figura 3.3(a) muestra que los residuos se encuentran alrededor de cero y no se observa ningún patrón claro. Esto es un indicio que el modelo está bien especificado y hay homocedasticidad. En la Figura 3.3(b) vemos que los residuos están alrededor de cero pero la variabilidad crece a medida que los valores ajustados aumenta. Esto es un indicador de heterocedasticidad. La Figura 3.3(c) también muestra un patrón de heterocedasticidad, la variabilidad aumenta hasta cierto punto y luego decrece. En la Figura 3.3(d) observamos que los residuos no fluctuan alrededor de cero, sino que siguen una curva. Esto nos que la relación entre la variable respuesta y las covariables no es lineal.

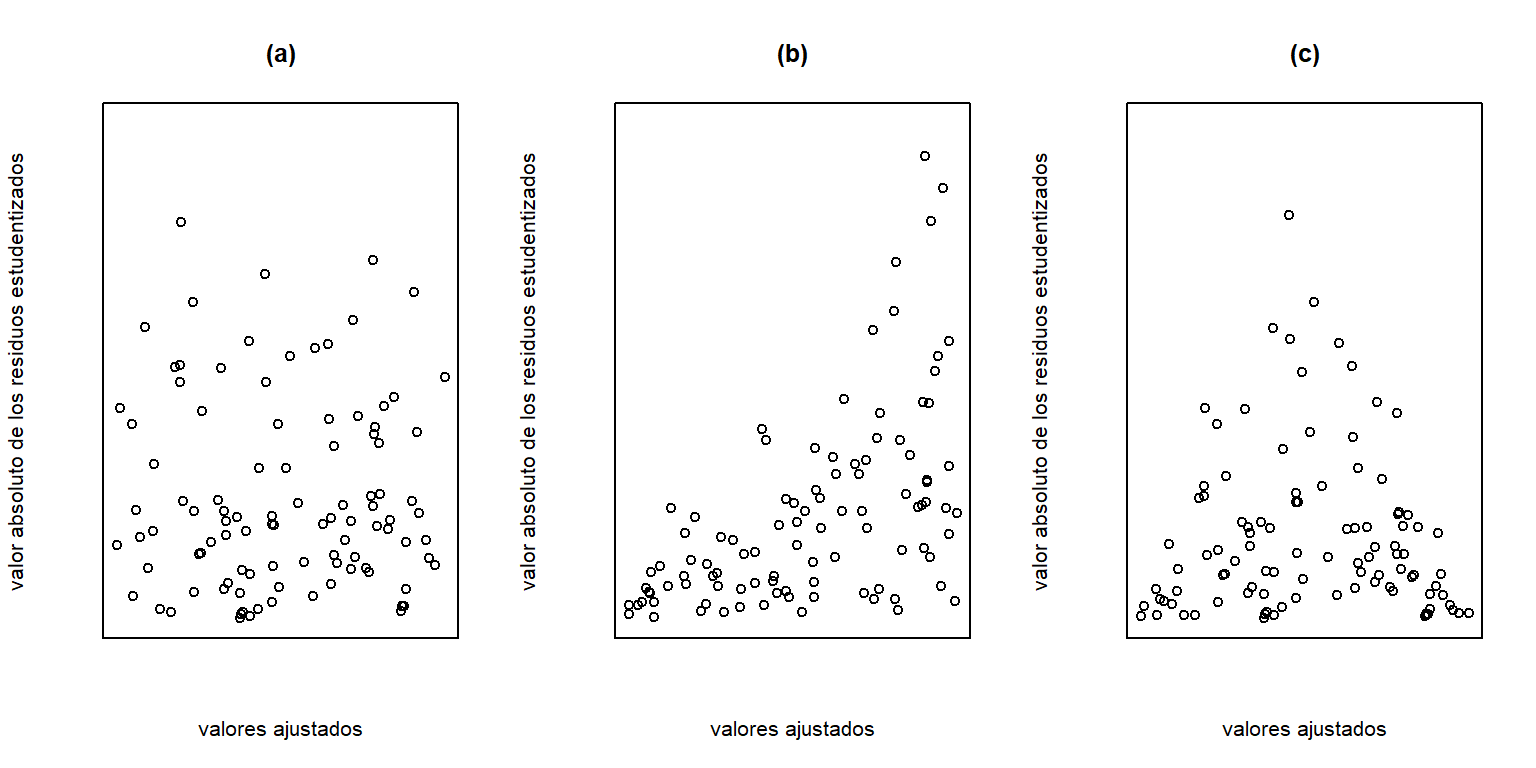
Figure 3.4: Ejemplos de posibles patrones de residuos (graficando el valor absoluto de los residuos).

Adicionalmente, para detectar más facilmente heterocedasticidad, se pueden graficar el valor absoluto de los residuos estudentizados (o al cuadrado) contra los valores ajustados (o las covariables). La Figura 3.4 muestra los mismos patrones pero graficando los residuos en valor absoluto. En las Figuras 3.4(b-c) se evidencia claramente la heterocedasticidad.

Bajo peso al nacer - gráfico de residuos

Para el modelo ajustado para los datos de peso al nacer, el gráfico de los residuos contra los valores ajustados se obtienen de la siguiente forma:

library(MASS)
res.stud.birthweight = studres(mod.birthweight)
mod.fit.birthweight = mod.birthweight$fitted.values
par(mfrow=c(1,2))
plot(mod.fit.birthweight,res.stud.birthweight, ylab='residuos estudentizados',
     xlab='valores ajustados',main='(a)')
abline(h=0,lty=2)
lines(lowess(res.stud.birthweight~mod.fit.birthweight), col = 2)
plot(mod.fit.birthweight,abs(res.stud.birthweight), 
     ylab='valor absoluto de los residuos estudentizados',
     xlab='valores ajustados',main='(b)')
lines(lowess(abs(res.stud.birthweight)~mod.fit.birthweight), col = 2)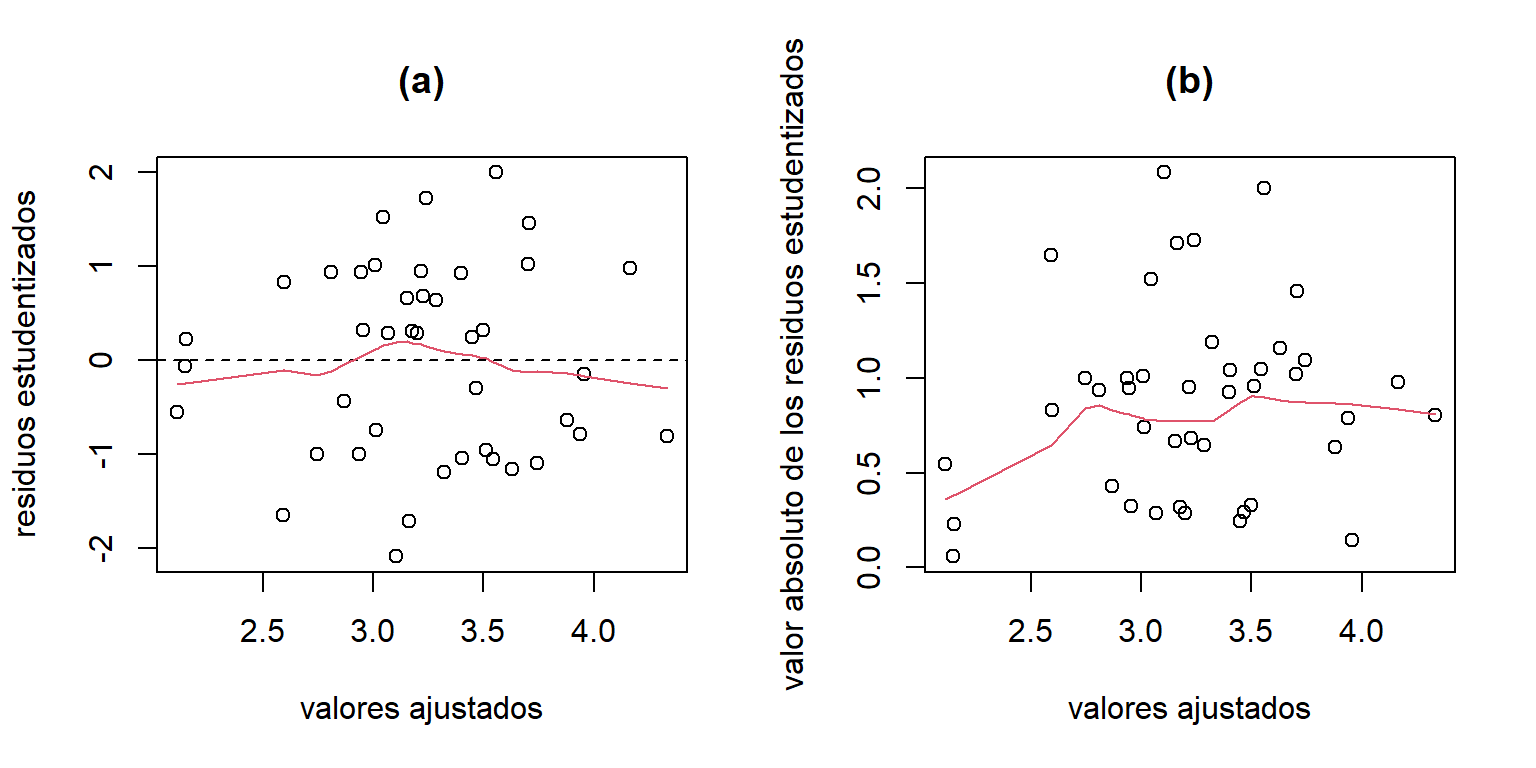

Figure 3.5: Datos de peso al nacer. Gráfico de los residuos estudentizados contra los valores ajustados.

La Figura 3.5(a) muestra que los residuos están alrededor de cero sin mostrar ningún patrón. Note que este gráfico es similar a la Figura 3.3(a). La línea roja es una suaviación LOWESS (Locally weighted scatterplot smoothing, más detalle ver Apéndice A.5 de Weisberg (2014)). Estas suavizaciones permiten ver fácilmente patrones de comportamiento. Aquí vemos que la suavización está cerca de la recta en cero sin mostrar ninguna tendencia o curvatura muy marcada. Por lo tanto, podemos afirmar que la relación entre el peso del recién nacido y las covariables propuesta es lineal. Además, no se observa un problema notorio de heterocedasticidad en ninguno de los dos gráficos de residuos.

3.4.2 Gráficos de residuos parciales

Los gráficos de residuos parciales permiten estudiar el efecto marginal de una covariable sobre la respuesta condicionado a que los demás regresores ya están en el modelo. En caso que el gráfico de los residuos muestre posibles curvaturas (por ejemplo, Figura 3.3(d)), los residuos parciales permiten verificar si estas se presentan debido a una covariable especifica.

Considere el modelo: \[ y_{i} = \beta_{0} +\beta_{1}x_{i1}+\beta_{2}x_{i2} + \ldots + \beta_{p-1}x_{i,p-1} + \varepsilon_{i}. \] Para calcular los residuos parciales, primero estimamos los parámetros \((\widehat{\beta}_{1},\ldots,\widehat{\beta}_{p-1})\) y los residuos ordinarios \((e_{1},\ldots,e_{n})\). Luego, los residuos parciales para la covariable \(x_{j}\) se obtienen de la siguiente forma: \[ e^{*}_{i}(y|x_{j}) = e_{i} - \widehat{\beta}_{j}x_{ij}. \] El gráfico de residuos parciales para la covariable \(x_{j}\) se obtiene graficando \(e^{*}_{i}(y|x_{j})\) contra \(x_{j}\). Si la covariable \(x_{j}\) entra al modelo linealmente, entonces el gráfico de residuos parciales debe mostrar una tendencia lineal. Por el contrario, si se observa una curva, \(x_{j}\) no entra al modelo de forma lineal.

Bajo peso al nacer - gráfico de residuos parciales

El gráfico de residuos parciales se obtiene así:

library(car)
par(mfrow=c(2,2))
crPlots(mod.birthweight,'age',xlab='edad gestacional')
crPlots(mod.birthweight,'motherage',xlab='edad de la madre')
crPlots(mod.birthweight,'mnocig',xlab='número de cigarrillos por mes')
crPlots(mod.birthweight,'mppwt',xlab='peso de la madre')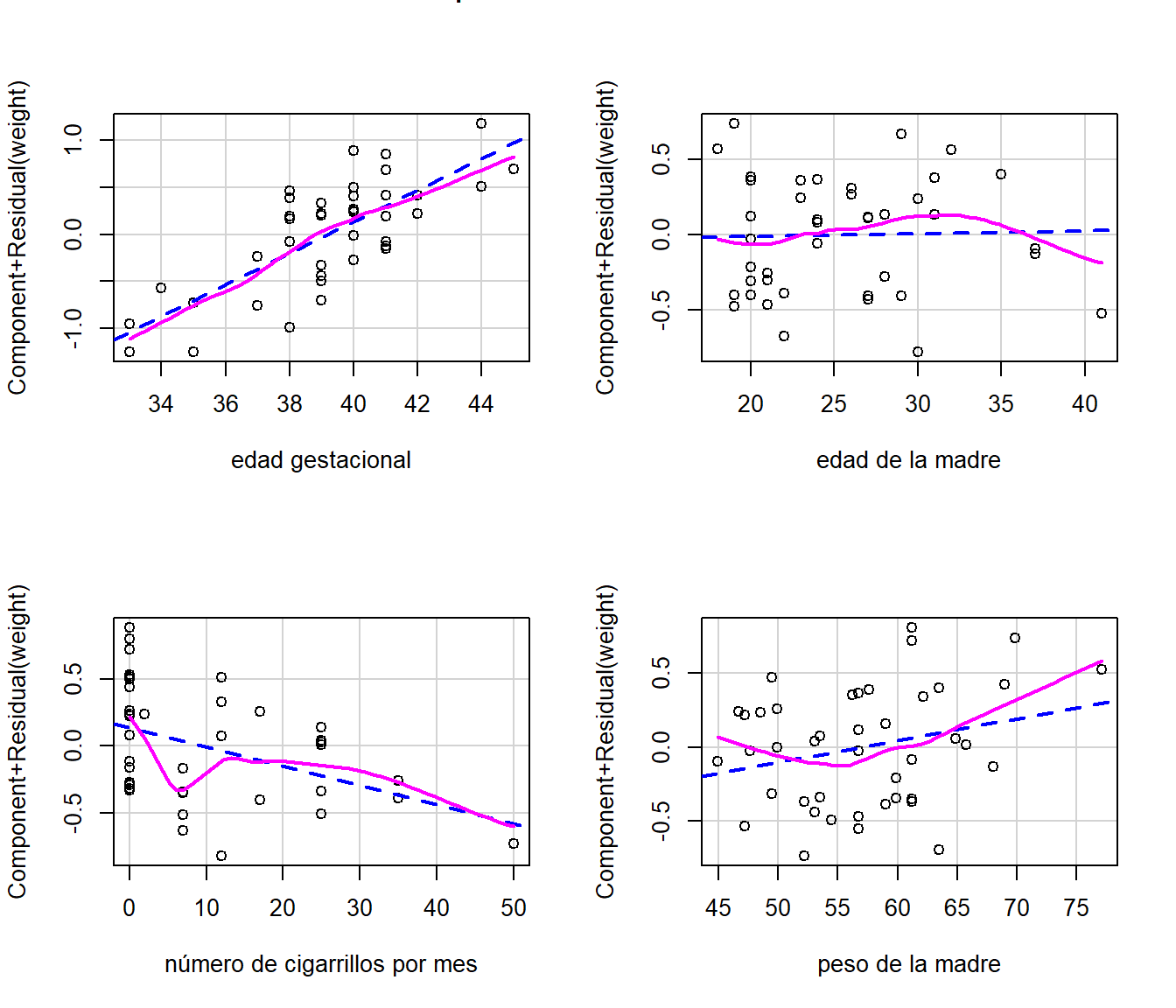

Figure 3.6: Datos de peso al nacer. Gráfico de los residuos parciales para cada covariable.

Igual que en el gráfico de residuos, los residuos parciales no muestran tendencias no lineales muy marcada. Por lo que se puede asumir que la relación entre el peso al nacer y las covariables es lineal.

3.4.3 Gráficos de normalidad

Los gráficos cuantil-cuantil (qqplot) comparan los cuantiles muestrales contra los cuantiles que se esperarían con la distribución de probabilidad asumida para los datos (cuantiles teóricos). En el caso de regresión lineal, estamos asumiendo que los errores del modelo siguen una distribución normal. Por lo tanto, debemos comparar los cuartiles muestrales de los residuos con los cuartiles teóricos que se esperarían bajo una distribución normal.

Sea \((x_{1},x_{2},\ldots,x_{n})\) una muestra aleatoría de la variable \(X\) con función de distribución desconocida \(F_{X}(x)\), y sean \((x_{[1]},x_{[2]},\ldots,x_{[n]})\) los estadísticos de orden (observaciones ordenadas de forma creciente). La función empirica de distribución es: \[ S_{n}(x_{[i]}) = \frac{i}{n} = \frac{\mbox{\# de observaciones }\leq x_{[i]}}{n}. \] Si asumimos que \(X\sim N(0,1)\), entonces los puntos \((x_{[i]},\Phi^{-1}\left\{S_{n}(x_{[i]})\right\})\), donde \(\Phi^{-1}()\) es la inversa de la función acumulativa de una normal estándar, deben seguir aproximadamente una línea recta.

La Figura 3.7 muestra diferentes patrones de gráficos de normalidad para datos generados a partir de tres distribuciones diferentes: normal estándar (derecha), exponencial con \(\lambda=1\) (centro), y \(t\)-Student con 2 grados de libertad (derecha). Aquí vemos que para los datos normales, los cuantiles muestrales y teóricos siguen aproximadamente la linea recta de referencia. Mientras que en los otros dos casos, los puntos se alejan en los extremos. En el caso de los datos exponenciales, es al lado izquierdo, mostrando que los datos presentan asímetrica. Mientras que con los datos \(t\)-Student, es a ambos lados, indicando que hay muchos valores en las colas (más de los esperados bajo normalidad).

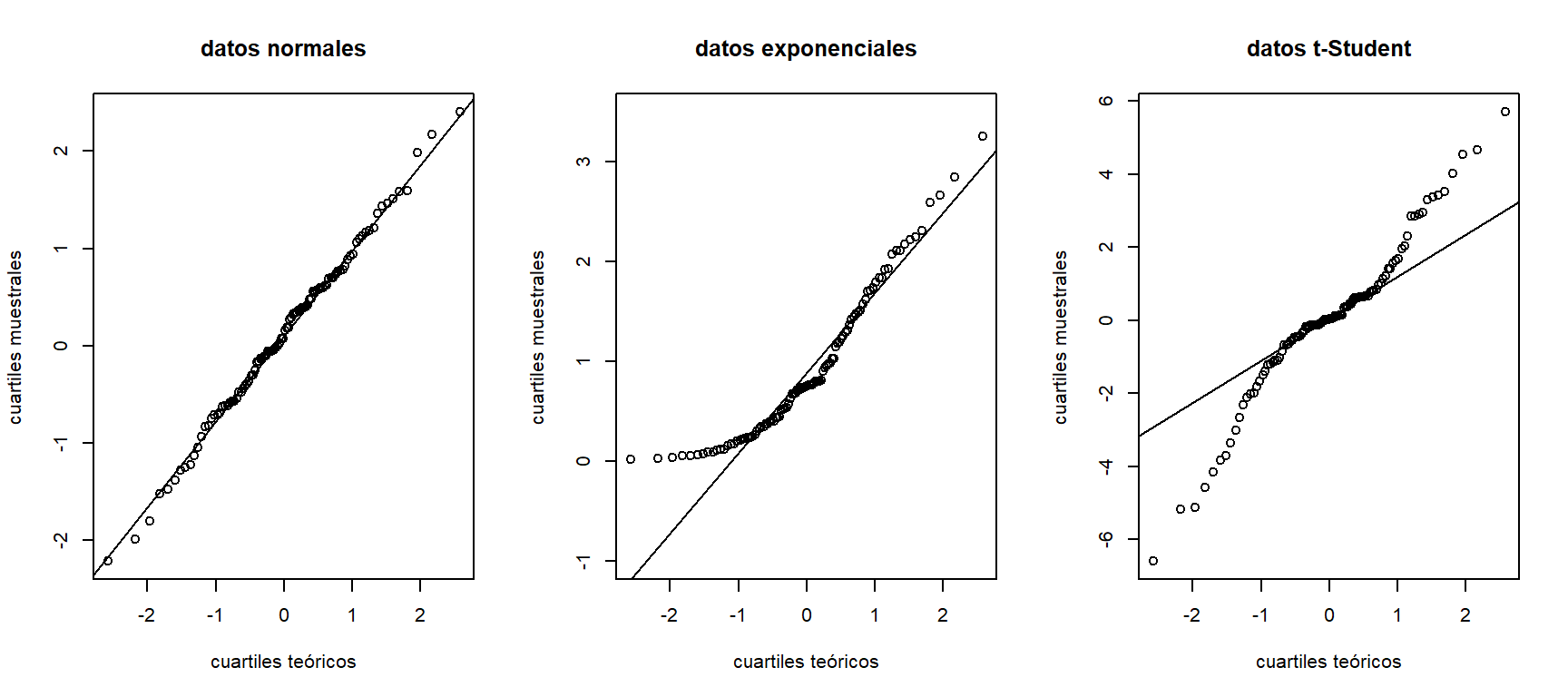
Figure 3.7: Gráficos de normalidad para datos aleatorios generados a partir de una distribución normal estándar (izquierda), exponencial (centro), y t-Student con 2 grados de libertad (derecha).

Bajo peso al nacer - gráfico de normalidad

El gráfico cuartil-cuartil de los residuos estudentizados se obtiene así:

car::qqPlot(mod.birthweight,xlab='cuantiles teóricos',ylab='residuos estudentizados',
       distribution = 'norm')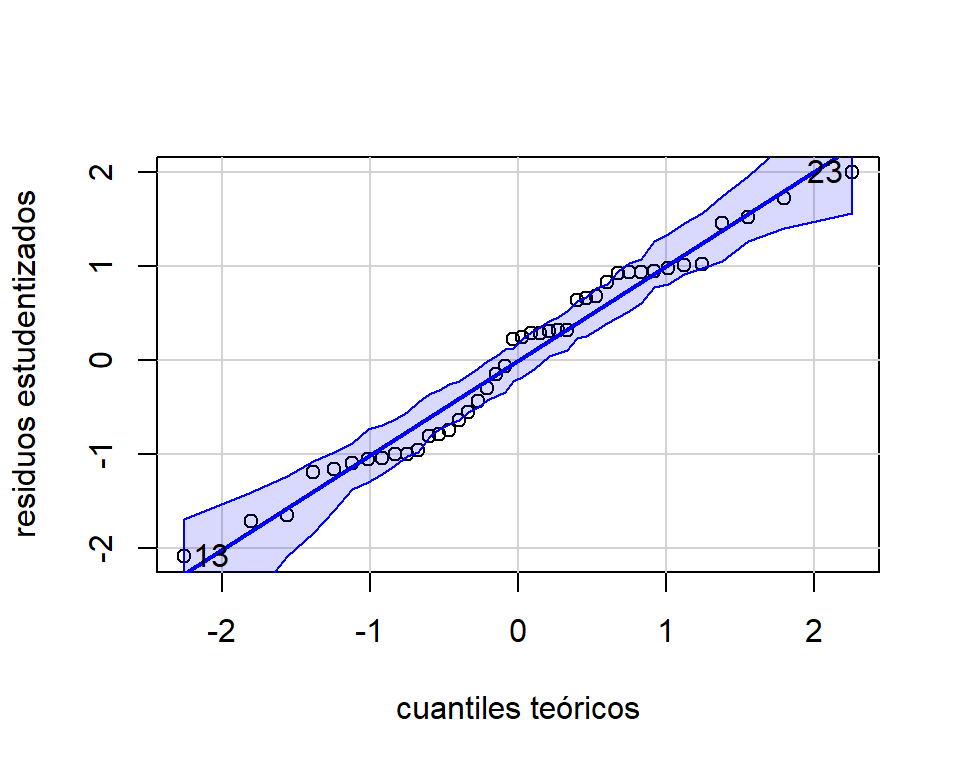

Figure 3.8: Datos de peso al nacer. Gráfico cuantil-cuantil para normalidad.

## [1] 13 23

Note que la función qqPlot incluye intervalos del \(95\%\) de confianza para los estadísticos de orden. Para más detalle de como se calculan, ver Sección 12.1.1 de Fox (2016).

La Figura 3.8 muestra que los puntos siguen de forma aproximada una línea recta. Además, la mayoría de los puntos están dentro de las bandas de confianza. Por lo tanto, se estaría cumpliendo el supuesto de normalidad.

3.4.4 Gráfico de residuos frente a el tiempo

Cómo se mencionó anteriormente, si las observaciones fueron tomadas de forma independiente, entonces se puede garantizar que los errores también lo sean. Para los datos del peso de los recién nacidos, tendríamos que asumir que los bebés fueron seleccionados de forma totalmente aleatoria, y así garantizar que los errores no están correlacionados. Por el contrario, los datos del consumo de helado fueron tomados a lo largo del tiempo (cada dos semanas), por lo que se puede presentar correlación temporal. Es decir, observaciones tomadas en tiempo cercanos se espera que estén altamente correlacionadas.

En caso de posible correlación temporal, se puede hacer un gráfico de los residuos con respecto al tiempo. Alternativamente, se puede hacer un gráfico de los residuos rezagados. Es decir, los residuos en el tiempo \(t\) (\(e_{t}\)) contra los residuos en el tiempo inmediatamente anterior \((e_{t-1})\).

La Figura 3.9 muestra diferentes patrones de comportamiento para residuos correlacionados temporalmente. En la columna (a) vemos el comportamiento de residuos incorrelacionados. Estos fluctúan alrededor de cero sin mostrar ningún patrón claro, además el gráfico de residuos rezagados no muestra niguna tendencia. Por el contrario, en las columnas (b) y (c) vemos patrones de comportamiento de residuos correlacionados de forma positiva y negativa, respectivamente. Cuando hay correlación positiva, los valores de los residuos que están cercanos en el tiempo tienden a ser muy similares, además el gráfico de los residuos rezagados muestra una relación positiva entre \(e_{t}\) y \(e_{t-1}\). Cuando la correlación es negativa, vemos que los residuos en el tiempo cambian de signo constantemente, además el gráfico de residuos rezagados muestra una tendencia negativa.

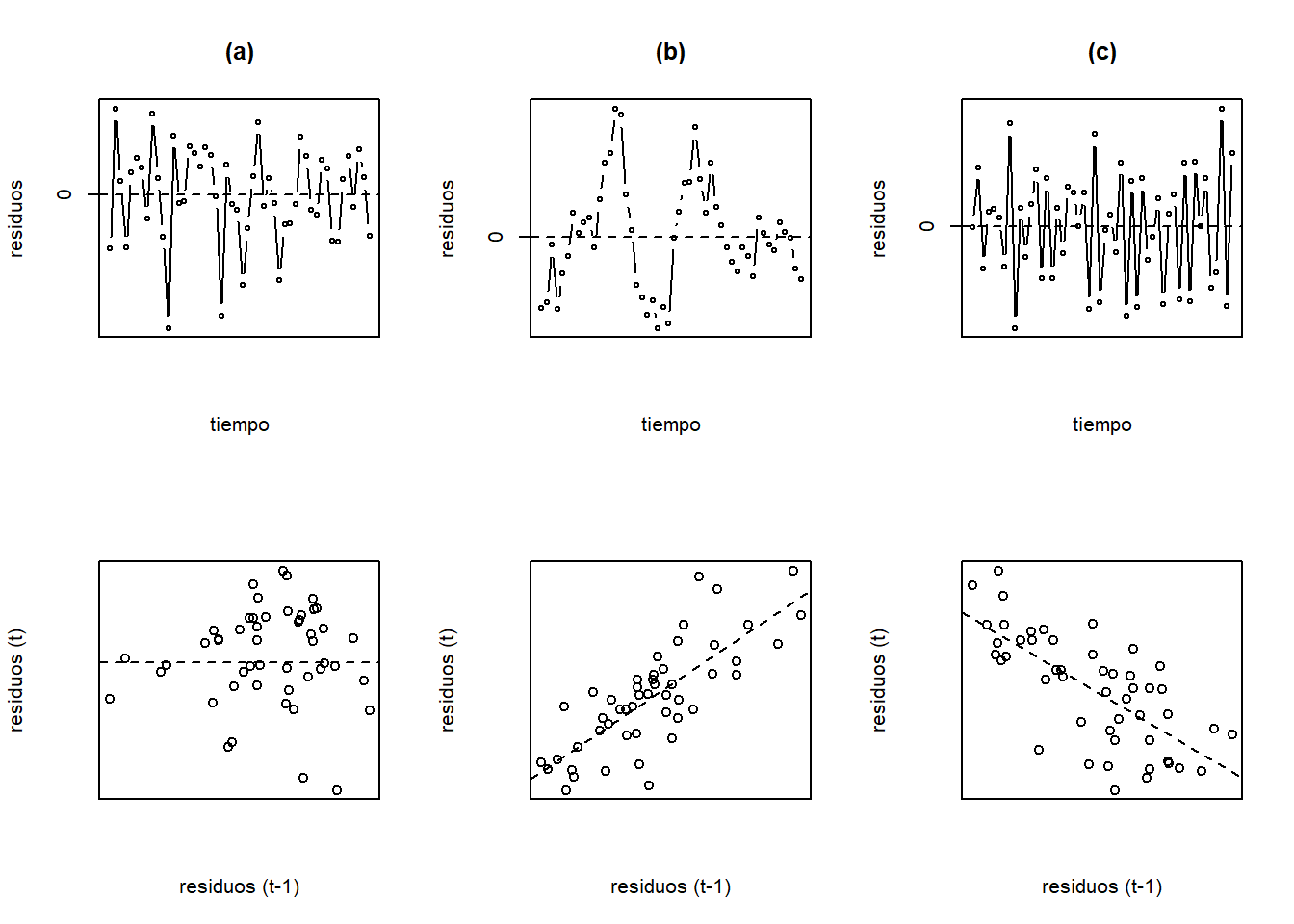
Figure 3.9: Patrones de correlación temporal de los residuos. En la columna (a) los residuos están incorrelacionados, (b) los residuos tienen correlación positiva, y en (c) los residuos tienen correlación negativa.

Consumo de helado - gráfico de los residuos contra el tiempo

Los gráficos de los residuos para el modelo ajustado a los datos de consumo de helado se observan en la Figura 3.10. Aquí vemos que la relación entre la variable respuesta y las covariables es aproximadamente lineal, no hay problemas de heterocedasticidad, y que los residuos siguen una distribución normal. Aunque se ve la presencia de un punto atípico.

res.stud.icecream = studres(mod.icecream)
mod.fit.icecream = mod.icecream$fitted.values
par(mfrow=c(1,2))
plot(mod.fit.icecream,res.stud.icecream, ylab='residuos estudentizados',
     xlab='valores ajustados')
abline(h=0,lty=2)
lines(lowess(res.stud.icecream~mod.fit.icecream), col = 2)
car::qqPlot(mod.icecream,xlab='cuantiles teóricos',ylab='residuos estudentizados',
       distribution = 'norm')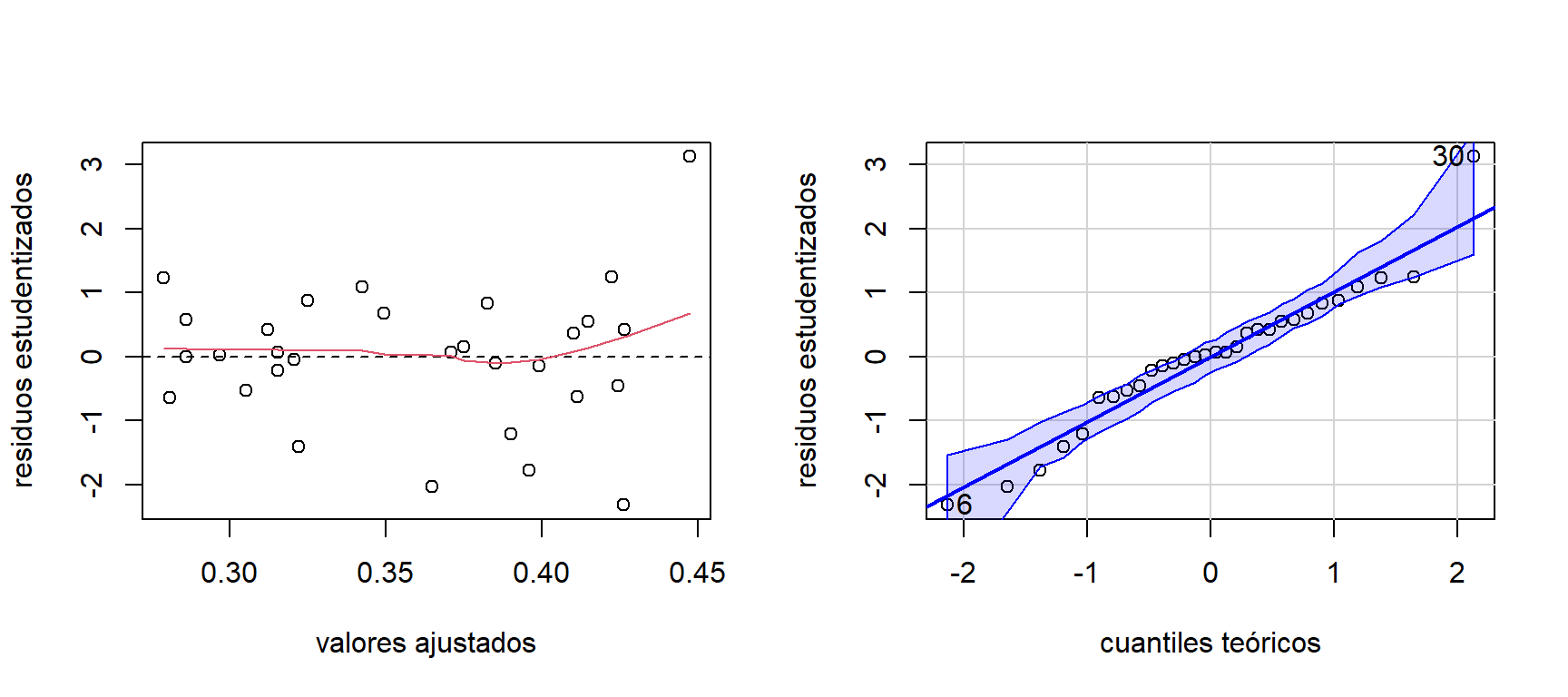

Figure 3.10: Datos de consumo de helado. Gráfico de los residuos estudentizados contra los valores ajustados (izquierda) y gráfico de normalidad (derecha).

## [1]  6 30

Dado que las observaciones del consumo de helado tienen un orden temporal (fueron tomadas cada 4 semanas), se pueden graficar los residuos contra el tiempo y de los residuos rezagados. Estos se pueden observar en la Figura 3.11. Aquí podemos ver que hay una correlación temporal positiva. Además, se tiene que \(cor(e_{t},e_{t-1}) = 0.605\).

par(mfrow=c(1,2))
plot(res.stud.icecream, ylab='residuos estudentizados',
     xlab='tiempo',type='b')
abline(h=0,lty=2)
plot(res.stud.icecream[-30],res.stud.icecream[-1], ylab='residuos estudentizados (t)',
     xlab='residuos estudentizados (t-1)')
abline(lm(res.stud.icecream[-1] ~ res.stud.icecream[-30]),lty=2)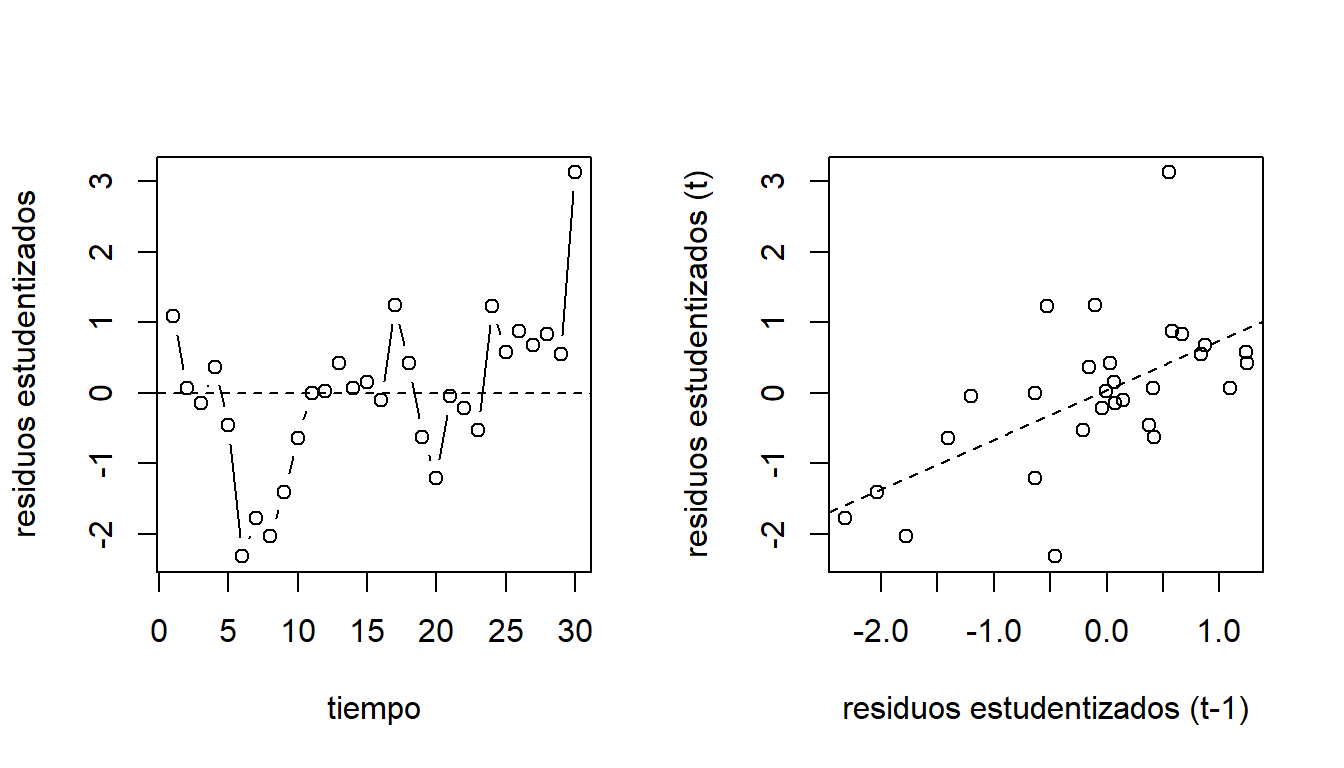

Figure 3.11: Datos de consumo de helado. Gráfico de los residuos estudentizados contra el tiempo (izquierda) y gráfico de residuos rezagados (derecha).

3.5 Pruebas de hipótesis para evaluar los supuestos

3.5.1 Prueba de falta de ajuste

El objetivo de la prueba de falta de ajuste es determinar si la relación entre la variable respuesta y las covariables puede asumirse cómo lineal. Hay que tener en cuenta que esta prueba es sensible a ajamientos de los supuestos de normalidad, varianza constante e independencia de los errores. Además, requiere que se tengan mútiple observaciones de \(y\) para diferentes niveles de \(\boldsymbol x\). Por ejemplo, el test puede implementarse en los datos de la longitud de los peces puesto que tenemos varios individuos con las mismas edades. En los otros casos, no es posible, por lo menos de forma exacta. El objetivo de estas observaciones replicadas es tener una estimación independiente de \(\sigma^{2}\).

En regresión lineal simple, suponga que se tienen \(n_{i}\) observaciones de la variable respuesta para el \(i\)-ésimo nivel de \(x_{i}\), para \(i=1,\ldots,m\), y denotemos \(y_{ij}\) como la \(j\)-ésima observación de la respuesta en \(x_{i}\), para \(j=1,\ldots,n_{i}\). Por lo tanto, tenemos \(n=\sum_{i=1}^{m}n_{i}\) observaciones en total. Esto permite que se puede descomponer la suma de cuadrados de los residuos en dos: \[ SS_{res} = SS_{PE} + SS_{LOF}, \] donde \(SS_{PE}\) y \(SS_{LOF}\) son la suma de cuadrados del error puro y falta de ajuste, respectivamente.

Para esto, primero observemos que los residuos se pueden descomponer así: \[\begin{equation} y_{ij} - \widehat{y}_{i} = (y_{ij} - \bar{y}_{i}) + (\bar{y}_{i} - \widehat{y}_{i}), \tag{3.1} \end{equation}\] donde \(\bar{y}_{i}\) es el promedio de las \(n_{i}\) observaciones en \(x_{i}\). Ahora, elevando al cuadrado ambos lados de (3.1), y sumando para todo \(i\) y \(j\), tenemos: \[\begin{equation} \begin{split} \sum_{i=1}^{m} \sum_{j=1}^{n_{i}} (y_{ij} - \widehat{y}_{i})^{2} &= \sum_{i=1}^{m}\sum_{j=1}^{n_{i}}(y_{ij}-\bar{y}_{i})^{2} + \sum_{i=1}^{m}n_{i}(\bar{y}_{i}-\widehat{y}_{i})^{2}, \\ SS_{res} &= SS_{PE} + SS_{LOF}. \end{split} \nonumber \end{equation}\]

Note que la suma de cuadrados de la falta de ajuste es una suma ponderada de las diferencias entre el promedio de las observaciones en cada nivel de \(x\) y el correspondiente valor ajustado. Por lo tanto, si la relación entre las variables es aproximadamente lineal, entonces se espera que \(SS_{LOF}\) sea cercana a cero.

Los grados de libertad de \(SS_{PE}\) y \(SS_{LOF}\) son \(\sum_{i=1}^{m}(n_{i}-1) = n-m\) y \(m-2\), respectivamente. De aquí se define el cuadrado medio del error puro y el cuadrado medio de la falta de ajuste:

\[ MS_{PE} = \frac{SS_{PE}}{n-m} \mbox{ y } MS_{LOF} = \frac{SS_{LOF}}{m-2}, \]

respectivamente. Si se cumple el supuesto de homocedasticidad, el valor esperado de \(MS_{PE}\) es: \[ E(MS_{PE}) = \frac{1}{n-m}E\left[ \sum_{j=1}^{n_{i}}(y_{ij} - \widehat{y}_{i})^{2} \right] = \frac{1}{n-m}\sum_{j=1}^{n_{i}} E\left[ (y_{ij}-\widehat{y}_{i})^{2} \right] = \frac{\sigma^{2}}{n-m}\sum_{j=1}^{n_{i}}(n_{i}-1) = \sigma^{2}. \] Es decir que el cuadrado medio del error puro es una estimación de \(\sigma^{2}\) independiente del ajuste del modelo.

Además, el valor esperado del cuadrado medio de la falta de ajuste es: \[ E(MS_{LOF}) = \sigma^{2} + \frac{\sum_{i=1}^{m}n_{i}\left[ E(y_{i}|x_{i}) - \beta_{0}-\beta_{1}x_{i} \right]^{2}}{m-2}. \] Por lo tanto, si la función de la media es lineal, entonces \(E(y_{i}|x_{i}) = \beta_{0}+\beta_{1}x_{i}\), y \(E(MS_{LOF}) = \sigma^{2}\). Si la función media no es lineal, entonces \(E(MS_{LOF}) > \sigma^{2}\)

La prueba de falta de ajuste plantea las siguiente hipótesis: \[ H_{0}: \mbox{el lineal modelo proporciona buen ajuste} \qquad H_{1}: \mbox{el modelo lineal no proporciona buen ajuste}, \] El estadístico de prueba es: \[ F_{0}=\frac{SS_{LOF}/(m-2)}{SS_{PE}/(n-m)} = \frac{MS_{LOF}}{MS_{PE}}. \] Si \(H_{0}\) es cierta, \(F_{0}\) sigue una distribución \(F_{m-2,n-m}\). Por lo tanto, se rechaza \(H_{0}\) (es decir, la función de regresión no es lineal) si \(F_{0} > F_{1-\alpha,m-2,n-m}\).

Como se mencionó antes, la prueba exige que se tenga múltiples observaciones para cada nivel de \(x\). Lo cuál es un gran desventaja. En caso que esto no ocurra, se puede hacer agrupaciones de los valores de las covariables (vecinos más cercanos), y considerarlas como repeticiones; de esta manera la prueba es aproximada.

3.5.1.1 Base de datos de la longitud de los peces - prueba de falta de ajuste

La Figura 3.12 muestra los gráficos de los residuos para el modelo ajustado a los datos de la longitud de los peces.

res.stud.bass = studres(mod.bass)
mod.fit.bass = mod.bass$fitted.values
plot(mod.fit.bass,res.stud.bass, ylab='residuos estudentizados',
     xlab='valores ajustados')
abline(h=0,lty=2)
lines(lowess(res.stud.bass~mod.fit.bass), col = 2)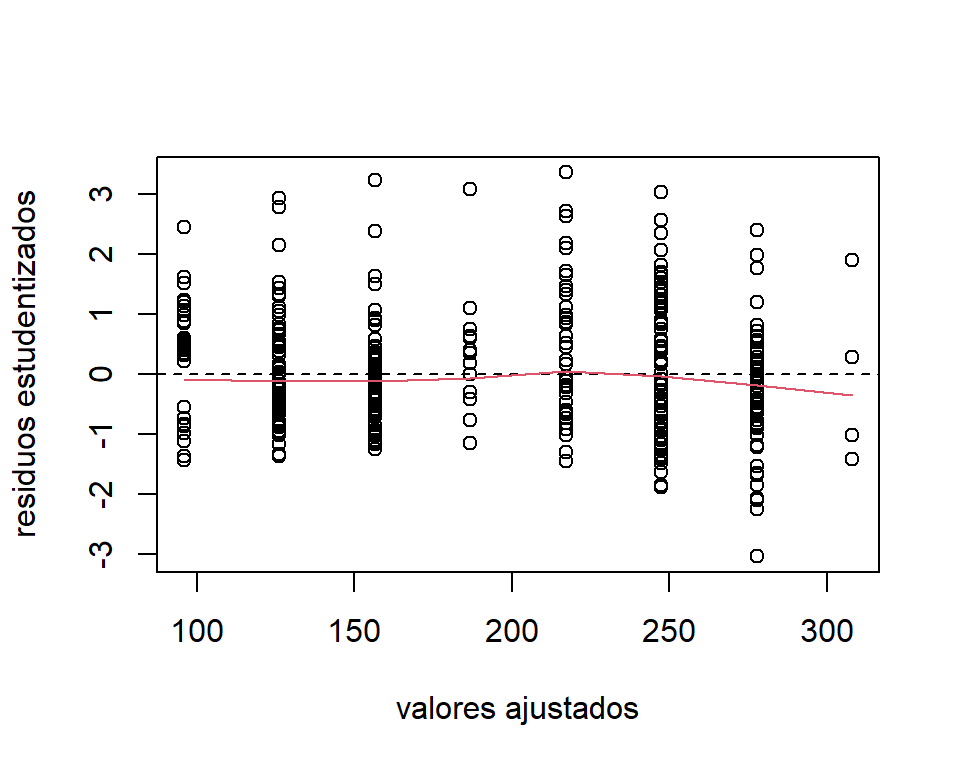

Figure 3.12: Datos de la longitud de los peces. Gráfico de los residuos estudentizados contra los valores ajustados.

La prueba de falta se ajuste se puede hacer usando la función anovaPE de la librería EnvStats:

library(EnvStats)
anovaPE(mod.bass)

##                 Df  Sum Sq Mean Sq   F value Pr(>F)    
## Age              1 1595359 1595359 1973.0736 <2e-16 ***
## Lack of Fit      6   10104    1684    2.0827 0.0541 .  
## Pure Error     431  348492     809                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

A partir del valor-\(p\) podemos concluir que no se rechaza \(H_{0}\), por lo tanto no hay suficiente evidencia para dudar del ajuste lineal propuesto.

3.5.2 Prueba de heterocedasticidad

Algunas pruebas de heterocedasticidad asumen que la varianza de los errores se compone de una parte constante y otra que varía según unas variables \((\boldsymbol z)\): \[ \sigma^{2}_{i} = f(\sigma^{2},\boldsymbol z_{i}), \] donde \(\sigma^{2}\) es la parte fija de la varianza, \(\boldsymbol z_{i}\) el conjunto de variables cuyos valores se asocian con los cambios en la varianza de los errores. Por lo general se asume que la función de varianza depende de algunas de las covariables del modelo, es decir que \(\boldsymbol z_{i}=\boldsymbol x_{i}\).

La prueba de Breusch-Pagan asume que la varianza es una función aditiva de las covariables: \[ \sigma^{2}_{i} = E(\varepsilon_{i}^{2}) = \gamma_{0} + \gamma_{1}x_{i1}+ \gamma_{1}x_{i2} + \ldots + \gamma_{p-1}x_{i,p-1}. \]

Por lo tanto, se pueden plantear las siguientes hipótesis: \[\begin{equation} \begin{split} H_{0}:& \gamma_{1} = \gamma_{2} = \ldots = \gamma_{p-1} = 0 \qquad \mbox{ (homocedasticidad)}, \\ H_{1}:& \gamma_{j}\neq 0 \mbox{ para algún }j=1,\ldots,p-1 \mbox{ (heterocedasticidad)}. \end{split} \nonumber \end{equation}\] Dado que los errores no son observables, el estadístico de prueba se construye a partir de los residuos del modelo estimado. Primero, se ajusta el siguiente modelo de regresión: \[ e_{i}^{2} = \gamma_{0} + \gamma_{1}x_{i1}+ \gamma_{1}x_{i2} + \ldots + \gamma_{p-1}x_{i,p-1} + \upsilon_{i}, \] donde se asume que \(\upsilon_{i}\sim N(0,\sigma^{2}_{\upsilon})\), y se obtiene el coeficiente de determinación \(R^{2}_{e}\).

si \(H_{0}\) es cierta, se tiene que \(W = n R^{2}_{e} \sim \chi^{2}_{p-1}\). Entonces, si \(W > \chi^{2}_{1-\alpha,p-1}\) se rechaza \(H_{0}\). Por lo tanto, hay heterocedasticidad.

El test de Breusch-Pagan sólo detecta formas lineales de heterocedasticidad. La prueba de White propone que la relación entre la varianza y las covariables es cuadrática: \[\begin{equation} \begin{split} \sigma^{2}_{i} &= \left(\gamma_{0}^{*} + \sum_{j=1}^{p-1}\gamma_{j}^{*}x_{ij}\right)^{2} \\ &= \gamma_{0} + \sum_{j=1}^{p-1}\gamma_{j}x_{ij} + \sum_{j=1}^{p-1}\gamma_{jj}x_{ij}^{2} + \sum_{j=1}^{p-1}\sum_{k \neq j}\gamma_{jk}x_{ij}x_{ik}. \end{split} \nonumber \end{equation}\] Dado que el número de parámetros del modelo se incrementa rápidamente a medida que tengamos más covariables, se pueden omitir las interacciones entre las covariables.

Por ejemplo si se tiene un modelo con tres covariables, se plantea la siguiente función para la varianza: \[ \sigma^{2}_{i} = \gamma_{0} + \gamma_{1}x_{i1} + \gamma_{1}x_{i2} + \gamma_{1}x_{i3} + \gamma_{4}x_{i1}^{2}+\gamma_{5}x_{i2}^{2} + \gamma_{6}x_{i3}^{2} + \gamma_{7}x_{i1}x_{i2} + \gamma_{8}x_{i1}x_{i3} + \gamma_{9}x_{i2}x_{i3} \] y las hipótesis son: \[\begin{equation} \begin{split} H_{0}:& \gamma_{1} = \gamma_{2} = \ldots = \gamma_{9} = 0 \qquad \mbox{ (homocedasticidad)}, \\ H_{1}:& \gamma_{j}\neq 0 \mbox{ para algún }j=1,\ldots,9 \mbox{ (heterocedasticidad)}. \end{split} \nonumber \end{equation}\] Para calcular el estadístico de prueba, primero ajustamos el siguiente modelo auxiliar: \[ e_{i}^{2} = \gamma_{0} + \gamma_{1}x_{i1} + \gamma_{1}x_{i2} + \gamma_{1}x_{i3} + \gamma_{4}x_{i1}^{2}+\gamma_{5}x_{i2}^{2} + \gamma_{6}x_{i3}^{2} + \gamma_{7}x_{i1}x_{i2} + \gamma_{8}x_{i1}x_{i3} + \gamma_{9}x_{i2}x_{i3} + \upsilon_{i}, \] y el coeficiente de determinación asociado \(R_{e}^{2}\). El estadístico de prueba es \(W=nR_{e}^{2}\), y rechazamos \(H_{0}\) si \(W > \chi^{2}_{1-\alpha,8}\).

Bajo peso al nacer - prueba de heterocedasticidad

En la prueba de White se asume que: \[\begin{equation} \begin{split} \sigma^{2}_{i} =& \gamma_{0} + \gamma_{1}\mbox{age}_{i} + \gamma_{2}\mbox{motherage}_{i} + \gamma_{3}\mbox{mnocig}_{i} + \gamma_{4}\mbox{mppwt}_{i}+ \\ & \gamma_{5}\mbox{age}_{i}^{2} + \gamma_{6}\mbox{motherage}_{i}^{2} + \gamma_{7}\mbox{mnocig}_{i}^{2} + \gamma_{8}\mbox{mppwt}_{i}^{2}. \end{split} \nonumber \end{equation}\] Dado que se tienen varias covariables, se omitieron las interacciones entre las covariables. Se plantean las siguientes hipótesis: \[\begin{equation} \begin{split} H_{0}:& \gamma_{1} = \gamma_{2} = \ldots = \gamma_{8} = 0 \qquad \mbox{ (homocedasticidad)}, \\ H_{1}:& \gamma_{j}\neq 0 \mbox{ para algún }j=1,\ldots,8 \mbox{ (heterocedasticidad)}. \end{split} \nonumber \end{equation}\] El ajuste del modelo auxiliar es:

res.stud.birthweight=mod.birthweight$residuals
mod.res.birthweight = lm(res.stud.birthweight^2 ~ age + motherage + mnocig + mppwt +
                           I(age^2) + I(motherage^2) + I(mnocig^2) + I(mppwt^2), 
                         data=birthweight)
summary(mod.res.birthweight)

## 
## Call:
## lm(formula = res.stud.birthweight^2 ~ age + motherage + mnocig + 
##     mppwt + I(age^2) + I(motherage^2) + I(mnocig^2) + I(mppwt^2), 
##     data = birthweight)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.20691 -0.08384 -0.01338  0.02286  0.41575 
## 
## Coefficients:
##                  Estimate Std. Error t value Pr(>|t|)  
## (Intercept)    -6.1348535  3.4447222  -1.781   0.0841 .
## age             0.2877513  0.1701394   1.691   0.1002  
## motherage      -0.0406689  0.0359059  -1.133   0.2655  
## mnocig          0.0024339  0.0051823   0.470   0.6417  
## mppwt           0.0433585  0.0435969   0.995   0.3272  
## I(age^2)       -0.0037481  0.0021924  -1.710   0.0967 .
## I(motherage^2)  0.0007444  0.0006445   1.155   0.2563  
## I(mnocig^2)    -0.0001672  0.0001335  -1.253   0.2192  
## I(mppwt^2)     -0.0003450  0.0003688  -0.935   0.3564  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1457 on 33 degrees of freedom
## Multiple R-squared:  0.2397, Adjusted R-squared:  0.05544 
## F-statistic: 1.301 on 8 and 33 DF,  p-value: 0.2772

Note que el estadístico \(F_{0}\) es pequeño y que las pruebas individuales sobre los coeficientes no son significativas. Esto es un indicio que \(H_{0}\) es cierta. El coeficiente de determinación es \(R_{e}^{2} = 0.24\). Entonces, \(W= 10.069\), con un valor-\(p\) asociado de \(0.2602\). Por lo tanto, no tenemos evidencia suficiente para determinar que hay heterocedasticidad.

La prueba se puede implementar directamente usando la función bptest de la librería lmtest llegando a los mismos resultados:

bptest(mod.birthweight, ~ age + motherage + mnocig + mppwt +
                           I(age^2) + I(motherage^2) + I(mnocig^2) + I(mppwt^2), 
                         data=birthweight)

## 
##  studentized Breusch-Pagan test
## 
## data:  mod.birthweight
## BP = 10.069, df = 8, p-value = 0.2602

Otras pruebas de heterocedasticidad que se pueden utilizar son:

• Prueba de Goldfeld–Quandt.
• Prueba de Barlett.
• Prueba de Cochran.
• Prueba de Hartley.

Las últimas tres pruebas requieren que se tengan múltiples observaciones para cada nivel de \(\boldsymbol x\). En caso que no se tengan repeticiones, es posible agruparlas por los vecinos más cercanos e implementar la prueba de forma aproximada.

3.5.3 Prueba de normalidad

Para probar normalidad podemos utilizar la prueba de Shapiro-Wilks.

Suponga que se tiene una muestra aleatoria \(x_{1},\ldots,x_{n}\) que se asumen sigue una distribución normal. Por lo cuál, se plantean las siguientes hipótesis: \[ H_{0}: \mbox{la distribución de }X \mbox{ es normal} \qquad H_{0}: \mbox{la distribución de }X \mbox{ no es normal} \] El estadístico de prueba propuestos por Shapiro y Wilks es: \[ W = \frac{ \sum_{i=1}^{[n/2]}a_{in}\left(x_{[n-i+1]}-x_{[i]}\right) }{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}, \] donde \((x_{[1]},x_{[2]},\ldots,x_{[n]})\) son los estadísticos de orden y los valores \(a_{in}\), así como los valores críticos, están dados en tablas tabuladas por los autores.

Bajo peso al nacer - prueba de normalidad

La prueba de Shapiro-Wilks para ajuste de los datos de peso al nacer es: lmtest:

shapiro.test(res.stud.birthweight)

## 
##  Shapiro-Wilk normality test
## 
## data:  res.stud.birthweight
## W = 0.96593, p-value = 0.2395

A partir de este resultado, no tenemos evidencia suficiente para rechazar que los errores se distribuyen normal. En esta función de R, el valor-\(p\) es calculado usando una aproximación.

Otras pruebas de normalidad que se pueden utilizar son:

• Modificaciones de la prueba Shapiro-Wilks, como son: D’agostino o Shapiro-Francia.
• Pruebas de bondad de ajuste generales, como son: Kolmogorov-Smirnov, Cramer-Von Mises, Anderson-Darling.

3.5.4 Prueba de correlación temporal de los errores

Cuando la correlación es debido a que las observaciones fueron tomadas en el tiempo, se puede asumir que hay autocorrelación. Aquí se asume que los errores que están separados \(t\) unidades de tiempo siempre tienen la misma correlación lineal. Además que la correlación disminuye a medida que las observaciones se separan en el tiempo.

El modelo de regresión, con errores autoregresivos de orden uno, es el siguiente: \[ y_{t} = \boldsymbol x_{t}'\boldsymbol \beta+ \varepsilon_{t}, \mbox{ con }\varepsilon_{t}= \phi\varepsilon_{t-1} + a_{t}, \] donde \(y_{t}\) y \(\boldsymbol x_{t}\) son la variable respuesta observada y el conjunto de covariables observadas en el tiempo \(t\), respectivamente, y \(\phi\) es el parámetro de autocorrelación \((|\phi| < 1)\). Además, se asume que \(a_{t} \sim N(0,\sigma^{2}_{a})\) y \(cov(a_{j},a_{k})=0\), para todo \(j \neq k\). A partir de estos resultados, se tiene que: \[ E(\varepsilon_{t}) = 0, V(\varepsilon_{t}) = \sigma^{2}_{a}\left( \frac{1}{1-\phi^2}\right), \mbox{ y } cov(\varepsilon_{t},\varepsilon_{t \pm k})= \phi^{k}\sigma^{2}_{a}\left( \frac{1}{1-\phi^2} \right). \] Por lo tanto, la correlación entre dos errores separados en \(k\) periodos de tiempo es \(cor(\varepsilon_{t},\varepsilon_{t\pm k}) = \phi^{k}\). Si \(\phi > 0\), los errores están correlacionados positivamente, pero la magnitud de la correlación disminuye a medida que los errores se separan más. Por otro lado, si \(\phi =0\) los errores están incorrelacionados.

La prueba de Durbin-Watson plantea las siguientes hipótesis: \[ H_{0}: \phi = 0 \mbox{ (independencia)} \qquad H_{1}:\phi \neq 0 \mbox{ (autocorrelación)} \] El estadístico de prueba es: \[ d = \frac{\sum_{t=2}^{T}\left( e_{t} - e_{t-1}\right)^{2}}{\sum_{t=1}^{T}e_{t}^{2}}. \] La distribución de probabilidad de \(d\), bajo \(H_{0}\), depende de la estructura de \(\boldsymbol X\) y es difícil de determinar. Por lo tanto, los valores críticos están tabulados para diferentes valores de significancia, tamaño de muestra y número de parámetros. Otra alternativa, usada por los paquetes estadísticos, es calcular la significancia a través de métodos de remuestreo y aproximaciones del estadístico de prueba a la distribución normal.

Ventas de helado - prueba de correlación temporal

La prueba de Durbin-Watson para ajuste de los datos de ventas de helado se puede hacer a través de la función durbinWatsonTest de la librería car:

durbinWatsonTest(mod.icecream,method='resample',reps=1000)

##  lag Autocorrelation D-W Statistic p-value
##    1       0.5412411      0.655856       0
##  Alternative hypothesis: rho != 0

Estos resultados muestran que hay correlación serial en los datos. Note que con esta función, el valor-\(p\) es calculado a partir de técnicas de remuestreo usando 1000 repeticiones.

3.6 Comentarios finales

Algunas consideraciones, muchas de ellas tomadas de Behar (2002):

• La efectividad de las pruebas formales depende del tamaño de la muestra. Si \(n\) es pequeño, la potencia es baja. Por lo tanto, es difícil detectar alejamientos de la hipótesis nula. Si por el contrario, la muestra es grande, la potencia es alta. Entonces, se rechaza la hipótesis nula ante cualquier alejamiento ligero.
• El incumplimiento de un supuesto puede reflejarse como el incumplimiento de otros. Por ejemplo, la falta de ajuste del modelo puede reflejarse como heterogeneidad de los errores y/o como correlación de los mismos.
• Hay que tener en cuenta que algunas pruebas de hipótesis suponen cierto alejamiento particular del supuesto que se quiere probar. Por ejemplo, el test de White asume que la varianza es una función cuadrática de las covariables. Por lo tanto si rechazamos esta prueba, no necesariamente podemos asegurar con total certeza que no hay heterocedasticidad. Es posible que la función de varianza tome otra forma.
• Adicionalmente, varias pruebas son muy sensibles al alejamiento de la suposición de normalidad. Es decir que, si los errores no son normalmente distribuidos, el nivel real de significancia puede ser muy diferente del especificado. Sin embargo, el rechazo de la hipótesis nula podría sugerir que al menos uno de los dos supuestos no se cumple.
• A la hora de validar el supuesto de normalidad de los errores se está interesado en saber si el alejamiento de ese modelo normal, es aceptable desde el punto de vista de la conservación de las propiedades y ventajas que se heredan de la normalidad. Las estimaciones de \(\widehat{\boldsymbol \beta}\) son generalmente robustas a desviaciones de la normalidad (Teorema del límite central).

References

Behar, Roberto. 2002. Validación de Supuestos En El Modelo de Regresión.

Fox, John. 2016. Applied Regression Analysis and Generalized Linear Models. Third Edition.

Weisberg, Sanford. 2014. Applied Linear Regression. Fourth edition.