Capítulo 1 Modelo lineal simple

Datos de grasa corporal

Un indicador de salud es el % de grasa corporal. Sin embargo, es una medida que es díficil de calcular de forma precisa. Hay varios métodos para ello, uno de estos requiere de pesaje bajo el agua (hidrodensitometría). Por lo que se quiere ajustar un modelo predictivo que dependa de mediciones que sean más fáciles de calcular, como son medidas antropométricas de diferentes partes del cuerpo.

La base de datos fat de la librería faraway contiene la edad, el peso, la estatura y 10 mediciones de circunferencias del cuerpo de 252 hombres. Además de estas medidas, se tiene el % de grasa coporal de estos hombres medido de forma precisa utilizando técnicas de pesaje bajo el agua.

La Figura 1.1 muestra la relación entre el % de grasa corporal y la circunferencia del abdomen (en cm). El % de grasa corporal es calculado a partir de la formula de Brozek.

library(faraway)
data(fat)
plot(brozek~abdom,data=fat,pch=20,xlab="circunferencia del abdomen (cm)",
     ylab='% de grasa corporal')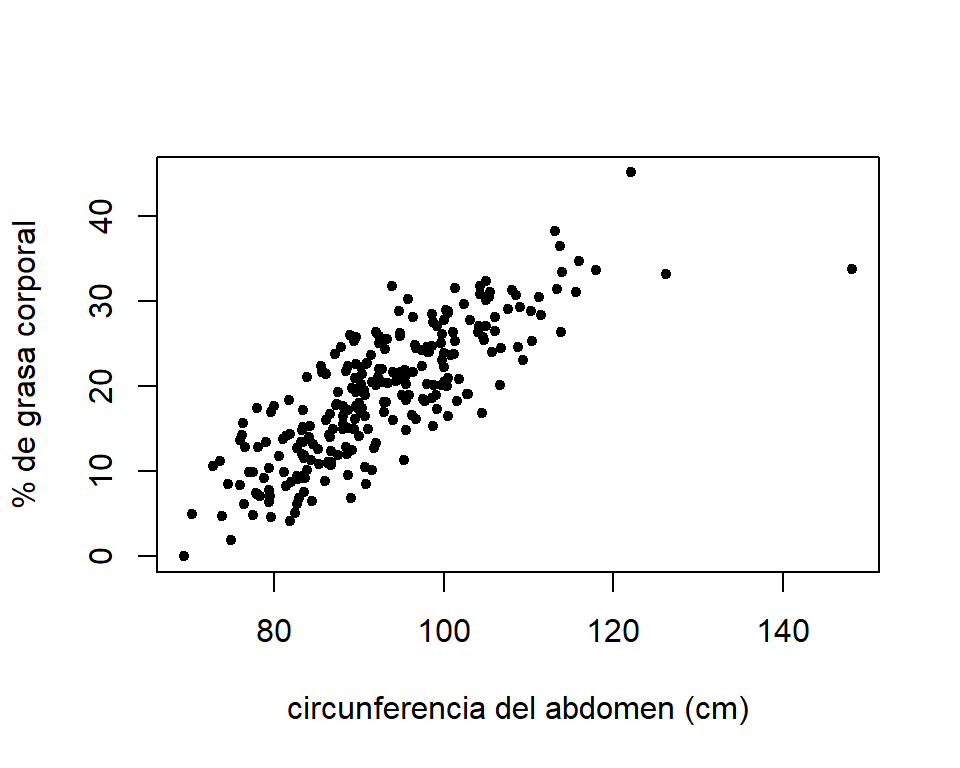

Figure 1.1: Gráfico de dispersion del % de grasa corporal y la circunferencia del abdomen.

Por medio de este gráfico vemos que hay una relación aproximadamente lineal positiva (la correlación es igual a 0.81). Es decir que los hombres con mayor grasa corporal presentan mayor circunferencia del abdomen. Por lo tanto, sería razonable describir el valor esperado del % de grasa corporal como una función lineal de la circunferencia del abdomen: \[ E(\mbox{grasa}|\mbox{abdom}=x) = \beta_{0} + \beta_{1}x. \]

Con este conjunto de datos podemos plantear las siguientes preguntas:

• Si comparamos hombres con una diferencia de 1cm (u otro valor) en la circunferencia del abdomen, ¿cómo cambiaría la media del % de grasa? ¿esa diferencia puede considerarse significativo?
• ¿Se puede predecir el % de grasa corporal por medio de la circunferencia del abdomen?

Estas preguntas se pueden resolver a partir del ajuste de un modelo lineal.

1.1 Regresion lineal simple

En un análisis de regresión simple estamos interesados en modelar una variable respuesta \(Y\) (variable dependiente) en función de una covariable \(X\) (regresor, variable independiente). Este modelo nos permite:

• Evaluar cómo cambia el valor esperado de \(Y\) debido a cambios en \(X\),
• Estimar el valor esperado de \(Y\) (o predecir) en función de \(X\).

1.2 Modelo lineal simple

Sea \((y_{i},x_{i})\) la i-ésima observación de la variable respuesta \((y)\) y la covariable \((x)\), para \(i=1,\ldots,n\), con \(n\) igual al número total de observaciones. El modelo lineal simple se puede expresar de la forma: \[ y_{i} = \beta_{0} + x_{i}\beta_{1}+\varepsilon_{i}, \] donde \(\beta_{0}\) es el intercepto, \(\beta_{1}\) es la pendiente y \(\varepsilon_{i}\) es el componente de error. Generalmente, los supuestos que acompañan este modelo son:

1. \(E(\varepsilon_{i}) = 0\),
2. \(V(\varepsilon_{i}) = \sigma^{2}\),
3. \(cov(\varepsilon_{i},\varepsilon_{j}) = 0\), para todo \(i \neq j\),
4. \(\varepsilon_{i}\) se distribuye normalmente.

Por lo tanto, \(\varepsilon_{i} \sim N(0,\sigma^{2})\).

A partir de (a) se tiene que: \[ E(Y|X=x_i) = \beta_{0} + x_i\beta_{1}. \] Entonces, para \(x=0\), el valor esperado de \(Y\) es igual a \(\beta_0\). Cuando \(X\) incrementa en una unidad (de \(x\) a \(x+1\)), el valor esperado de \(Y\) aumenta en: \[ E(Y|X=x+1) - E(Y|X=x) = \beta_{0} + (x+1)\beta_{1} - (\beta_{0} + x\beta_{1}) = \beta_{1}. \] Lo que indica que \(\beta_{1}\) representa el cambio en el valor esperado de \(Y\) por un aumento unitario en \(X\).

Dado (b), tenemos que \(V(Y|X=x_{i}) = \sigma^{2}\). Es decir que para cualquier valor de \(x\), la varianza de \(Y\) es la misma (homocedasticidad). Puesto que los errores están incorrelacionados (c), entonces las observaciones de \(Y\) también lo están, \(cov(Y_i,Y_j)=0\) para todo \(i \neq j\).

Debido a (d), tenemos que la variable respuesta también se distribuye de forma normal. Específicamente, tenemos que: \(y_{i}|x_i \sim N(\beta_{0} + \beta_{1}x_i, \sigma^{2})\).

El proceso de generación de datos del modelo de regresión lineal se ilustra en la Figura 1.2. El valor esperado de \(Y|X\) está representado por la linea negra. Tenemos que, cada observación de \(y\) (puntos negros) es una realización de la distribución de \(Y|X=x_{i} \sim N(\beta_{0}+\beta_{1}x_{i},\sigma^{2})\) (curvas rojas). En esté ejemplo, suponemos que \(\beta_{0}=0\), \(\beta_{1}=1\), y \(\sigma=0.1\).

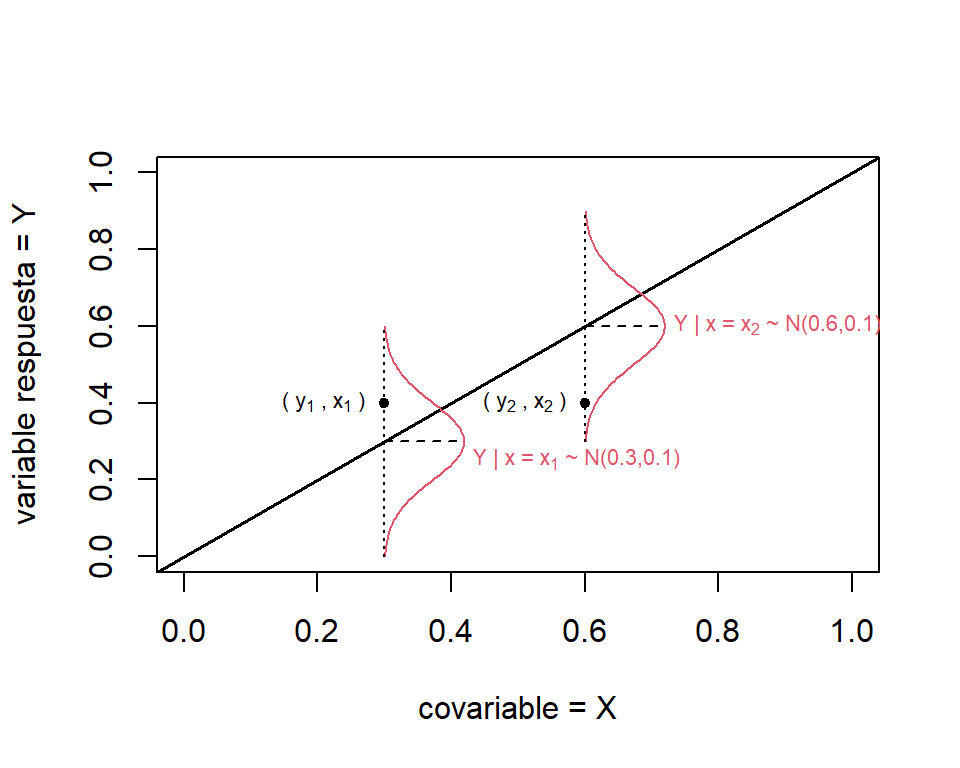
Figure 1.2: Proceso generador datos del modelo lineal simple.

1.3 Estimación de los parámetros

Los parámetros \(\beta_{0}\) y \(\beta_{1}\) son desconocidos y deben estimarse a partir de los datos. Para esto utilizamos el método de mínimos cuadrados ordinarios (MCO).

La función objetivo es la siguiente: \[\begin{equation} S(\beta_{0},\beta_{1}) = \sum_{i=1}^{n} \left[ y_{i} - (\beta_{0} + \beta_{1}x_{i}) \right]^{2}. \tag{1.1} \end{equation}\] Entonces, tenemos que encontrar la combinación de \(\beta_{0}\) y \(\beta_{1}\) que minimizan (1.1). Para esto, primero debemos derivar \(S(\beta_{0},\beta_{1})\) con respecto a \(\beta_{0}\) y \(\beta_{1}\), e igualar estas ecuación a cero. De esta forma obtenemos las ecuaciones normales: \[\begin{equation} \frac{\partial S(\beta_{0},\beta_{1})}{\partial \beta_{0}} = - 2\sum_{i=1}^{n}\left(y_{i}-\beta_{0}-\beta_{1}x_{i} \right), \tag{1.2} \end{equation}\] y \[\begin{equation} \frac{\partial S(\beta_{0},\beta_{1})}{\partial \beta_{1}} = - 2\sum_{i=1}^{n}\left(y_{i}-\beta_{0}-\beta_{1}x_{i} \right)x_{i}. \tag{1.3} \end{equation}\]

Los estimadores por MCO (\(\widehat{\beta}_{0}\) y \(\widehat{\beta}_{1}\)) se obtienen resolviendo el sistema de ecuaciones (1.2) y (1.3): \[ \widehat{\beta}_{0} = \bar{y} - \widehat{\beta}_{1}\bar{x}, \] y \[ \widehat{\beta}_{1} = \frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sum_{i=1}^{n}(x_{i}-\bar{x})^2} = \frac{S_{xy}}{S_{xx}} = cor(X,Y)\frac{s_{Y}}{s_{X}}, \] donde \(s_{X}\) y \(s_{Y}\) son las desviaciones estándar muestrales de \(X\) y \(Y\).

La diferencia entre el valor observado \((y_{i})\) y el valor ajustado correspondiente \((\widehat{y}_{i})\) es llamado residuo: \[ e_{i}= y_{i} - (\widehat{\beta}_{0} + \widehat{\beta}_{1}x_{i}) = y_{i}-\widehat{y}_{i}. \] La Figura 1.3 presenta los residuos de forma gráfica. Estos juegan un papel importante para la evaluar la bondad del ajuste del modelo (detectar posibles desviaciones a los supuestos asumidos).

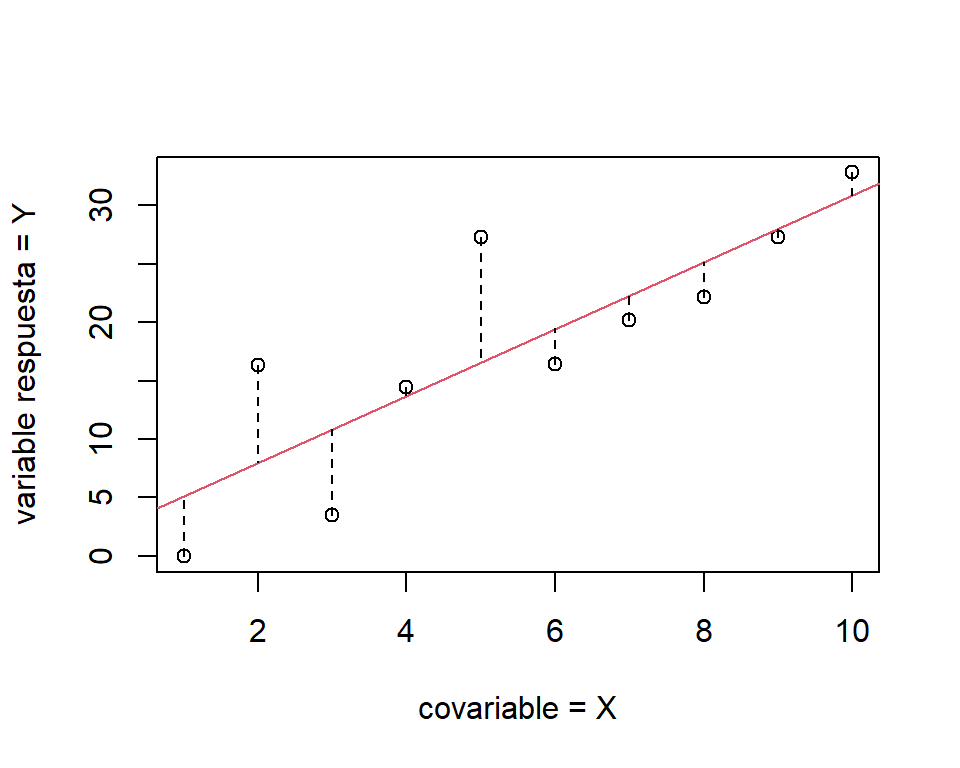
Figure 1.3: Diagrama gráfico de un ajuste por MCO. La recta roja representa la estimación por MCO, y las lineas discontinuas verticales entre los puntos observados y la recta estimada son los residuos.

1.4 Estimación de \(\sigma^{2}\)

La estimación de \(\sigma^{2}\) se hace a partir de la suma de cuadrados de los residuos: \[ SS_{res} = \sum_{i=1}^{n}e^{2}_{i} = \sum_{i=1}^{n} (y_{i}-\widehat{\beta}_{0} - \widehat{\beta}_{1}x_{i})^{2}. \] El valor esperado de \(SS_{res}\) es \(E(SS_{res})=(n-2)\sigma^{2}\) (Para el caso de regresión múltiple, ver Sección C.3 de Montgomery, Peck, and Vining (2012)). Por lo tanto, un estimador insesgado de \(\sigma^{2}\) es: \[ \widehat{\sigma}^{2} = \frac{SS_{res}}{n-2} = MS_{res}. \] La cantidad \(MS_{res}\) es llamada cuadrado medio de los residuos.

Datos de grasa corporal. Modelo y estimación de parametros

Asumiendo brozek\(_i\) como el % de grasa corporal del \(i\)-ésimo hombre, y abdom\(_i\) como la circunferencia de su abdomen en centímetros, se propone el siguiente modelo: \[\begin{equation} \mbox{brozek}_{i}= \beta_{0} + \beta_{1}\mbox{abdom}_{i} + \varepsilon_{i}, \tag{1.4} \end{equation}\] donde \(\varepsilon_{i} \sim N(0,\sigma^{2})\) y \(cov(\varepsilon_{i},\varepsilon_{j})=0\) para todo \(i \neq j\).

En R, la estimación por MCO se realiza a través de la función lm:

mod = lm(brozek~abdom, data=fat)
mod

## 
## Call:
## lm(formula = brozek ~ abdom, data = fat)
## 
## Coefficients:
## (Intercept)        abdom  
##    -35.1966       0.5849

De aquí obtenemos que \(\widehat{\beta}_{0} =-35.2\) y \(\widehat{\beta}_{1} =0.58\). Note que la estimación del intercepto es negativa, lo que es físicamente imposible. Además, tampoco tiene sentido una circunferencia del abdomen de 0cm. Por lo cual, este parámetro no tiene interpretación en este caso. \(\beta_{0}\) solo tiene interpretación cuando las observaciones de la covariable están alrededor de cero. En este caso, las circunferencias del abdomen están entre 69.4cm y 148.1cm.

A partir de \(\widehat{\beta}_{1}\), podemos concluir que la circunferencia del abdomen tiene un efecto positivo sobre el % de grasa corporal (el coeficiente estimado es positivo). La diferencia promedio en el % de grasa, comparando hombres con una diferencia de un centímetro en la circunferencia del abdomen, es de 0.58%. Si la diferencia es de 10cm, entonces la diferencia en media es de 5.8%.

La representación gráfica del modelo estimado se presenta en la Figura 1.4.

plot(brozek~abdom,data=fat,pch=20,xlab="circunferencia del abdomen(cm)",
     ylab='% de grasa corporal')
abline(mod,lwd=2)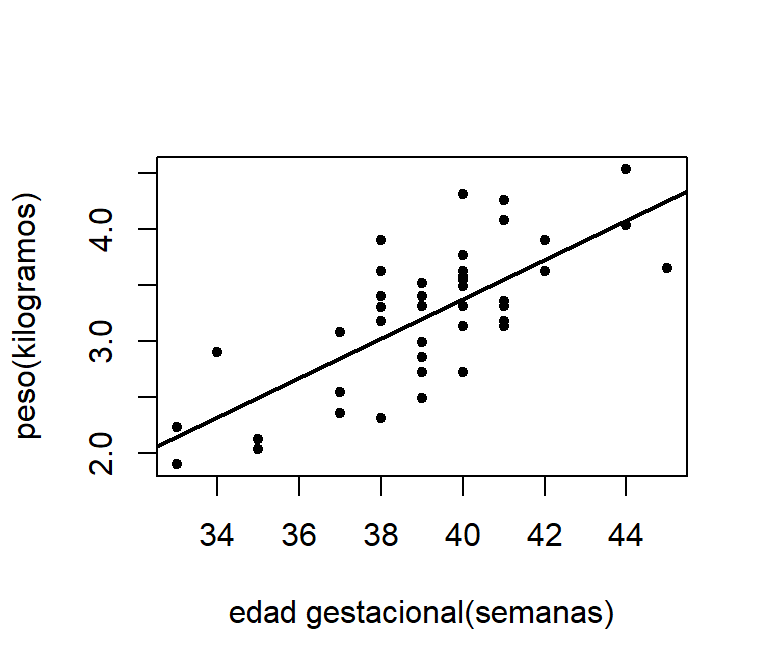

Figure 1.4: Gráfico de dispersion del peso del % de grasa corporal y la circunferencia del abdomen. La linea representa la estimación por MCO.

La estimación de \(\sigma\) es:

 sqrt(sum(mod$residuals^2)/40)

## [1] 11.28598

1.5 Propiedades de los estimadores por MCO

Los estimadores de \(\widehat{\beta}_{0}\) y \(\widehat{\beta}_{1}\) son una combinación lineal de las observaciones: \[\begin{equation} \widehat{\beta}_{1} = \sum_{i=1}^{n} \frac{(x_{i}-\bar{x})(y_{i}-\bar{y})}{S_{xx}} = \sum_{i=1}^{n} \frac{(x_{i}-\bar{x})}{S_{xx}}y_{i} = \sum_{i=1}^{n}c_{i}y_{i}. \tag{1.5} \end{equation}\] y \[ \widehat{\beta}_{0} = \bar{y} - \widehat{\beta}_{1}\bar{x} = \sum_{i=1}^{n}\left( \frac{1}{n} - c_{i}\bar{x} \right)y_{i} = \sum_{i=1}^{n}d_{i}y_{i}. \] Se puede verificar que \(\sum_{i=1}^{n}c_{i}=0\) y \(\sum_{i=1}^{n}c_{i}x_{i}=1\).

Los valores ajustados también son combinaciones lineales de los datos: \[ \widehat{y}_{i} = \widehat{\beta}_{0} + \widehat{\beta}_{1}x_{i} = \sum_{i=1}^{n}(d_{i}+c_{i}x_{i})y_{i}. \] Puesto que los estimadores de \(\beta_{0}\) y \(\beta_{1}\) dependen de los errores, estos también son variables aleatorias. Por lo tanto debemos calcular el valor esperado y varianza de \(\widehat{\beta}_{0}\) y \(\widehat{\beta}_{1}\).

Si \(E(\varepsilon_i)=0\), tenemos que el valor esperado de \(\widehat{\beta}_{1}\) es: \[\begin{equation} \begin{split} E(\widehat{\beta}_{1}) &= E\left( \sum_{i=1}^{n}c_{i}y_{i} \right) = \sum_{i=1}^{n}c_{i}E(y_{i}) = \sum_{i=1}^{n} c_{i}(\beta_{0} + \beta_{1}x_{i}) \\ &=\beta_{0}\sum_{i=1}^{n}c_{i} + \beta_{1}\sum_{i=1}^{n}c_{i}x_{i} = \beta_{1}, \end{split} \nonumber \end{equation}\] y el valor esperado de \(\widehat{\beta}_{0}\) es: \[\begin{equation} \begin{split} E(\widehat{\beta}_{0}) &= E\left(\bar{y} - \widehat{\beta}_{1}\bar{x} \right) = \frac{1}{n}\sum_{i=1}^{n}E(y_{i}) - \beta_{1}\bar{x} \\ &= \frac{1}{n}\sum_{i=1}^{n}\left(\beta_{0} + \beta_{1}x_{i}\right) - \beta_{1}\bar{x} = \beta_{0}. \end{split} \nonumber \end{equation}\]

Es decir que \(\widehat{\beta}_{0}\) y \(\widehat{\beta}_{1}\) son estimadores insesgado de \(\beta_{0}\) y \(\beta_{1}\),respectivamente.

Si \(V(\varepsilon_i) = \sigma^2\) y \(cov(\varepsilon_i,\varepsilon_j)=0\), la varianza de \(\widehat{\beta}_{1}\) y \(\widehat{\beta}_{0}\) son: \[ V(\widehat{\beta}_{1})= V \left( \sum_{i=1}^{n}c_{i}y_{i}\right) = \sum_{i=1}^{n}c_{i}^{2}V(y_{i}) = \sigma^{2}\sum_{i=1}^{n}c_{i}^{2} = \frac{\sigma^{2}}{S_{xx}}, \] y \[\begin{equation} \begin{split} V(\widehat{\beta}_{0}) &= V \left( \bar{y} - \widehat{\beta}_{1}\bar{x}\right) = V (\bar{y}) + \bar{x}^{2}V(\widehat{\beta}_{1}) - 2\bar{x}Cov(\bar{y},\widehat{\beta}_{1}) \\ &= \sigma^{2} \left(\frac{1}{n} + \frac{\bar{x}^{2}}{S_{xx}} \right), \end{split} \nonumber \end{equation}\] respectivamente. Finalmente, la covarianza entre \(\widehat{\beta}_{0}\) y \(\widehat{\beta}_{1}\) es: \[\begin{equation} \begin{split} Cov(\widehat{\beta}_{0},\widehat{\beta}_{1}) &= Cov\left(\bar{y} - \widehat{\beta}_{1}\bar{x}, \widehat{\beta}_{1} \right) = Cov\left( \bar{y}, \widehat{\beta}_{1}\right) - \bar{x}V\left(\widehat{\beta}_{1}\right) \\ &= - \sigma^{2}\frac{\bar{x}}{S_{xx}}. \end{split} \nonumber \end{equation}\]

Si se cumple que \(E(\varepsilon_{i}) = 0\), \(V(\varepsilon_{i}) = \sigma^{2}\) y \(cov(\varepsilon_{i},\varepsilon_{j})=0\), se puede probar que los estimadores por MCO son insesgados y de varianza mínima (teorema de Gauss-Markov). Para la demostración en el caso de regresión múltiple, ver Sección C4 de Montgomery, Peck, and Vining (2012). Esto quiere decir que, comparado con todos los posibles estimadores insesgados que son combinación lineal de las observaciones, \(\widehat{\beta}_{0}\) y \(\widehat{\beta}_{1}\) tienen las varianzas más pequeñas. Por esto, los estimadores por MCO son considerados los mejores estimadores lineales insesgados.

1.6 Inferencia

También podemos hacer pruebas de hipótesis e intervalos de confianza para los parámetros del modelo y/o pronósticos.

Por ejemplo, en los datos de la grasa corporal podemos estar interesados en evaluar si el efecto de la circunferencia del abdomen es positivo sobre el % de grasa corporal. Por lo tanto, debemos probar si \(\beta_{1} > 0\) (u cualquier otro valor). También podríamos estar interesados en el valor esperado del % de grasa corporal para cierto valor específico de circunferencia del abdomen, por ejemplo 80cm Entonces, podemos calcular un intervalo de confianza para \(E(Y|X=80)\).

1.6.1 Pruebas de hipótesis

Suponga la siguiente hipótesis: \[\begin{equation} H_{0}: \beta_{1} = \beta_{10} \mbox{ } H_{1}: \beta_{1} \neq \beta_{10}. \tag{1.6} \end{equation}\] Dado que \(\widehat{\beta}_{1}\) es una combinación lineal de \(y_{i}\) (1.5), podemos concluir que: \[ \widehat{\beta}_{1} \sim N\left(\beta_{1}, \frac{\sigma^{2}}{S_{xx}}\right). \] Además, \[\begin{equation} t_{0} = \frac{\widehat{\beta}_{1}-\beta_{10}}{\sqrt{\frac{MS_{res}}{S_{xx}}}}\sim t_{n-2}. \tag{1.7} \end{equation}\] Por lo tanto, \(t_{0}\) es el estadístico de prueba para las hipótesis (1.6). Entonces, rechazamos \(H_{0}\) si \(|t_{0}| \ge t_{1-\alpha/2,n-p}\) (o por medio del valor-\(p\) asociado).

De igual forma, para evaluar: \[ H_{0}: \beta_{0} = \beta_{00} \mbox{ } H_{1}: \beta_{0} \neq \beta_{00}, \] el estadístico de prueba es: \[\begin{equation} t_{0} = \frac{\widehat{\beta}_{0}-\beta_{00}}{\sqrt{MS_{res}\left(\frac{1}{n}+\frac{\bar{x}^{2}}{S_{xx}} \right)}} \sim t_{n-2}. \tag{1.8} \end{equation}\]

1.6.2 Análisis de varianza

El análisis de varianza se basa en la partición de la variabilidad total de la variable respuesta \(y\) en dos componentes, uno debido al modelo ajustado y otro al error. Primero, empecemos con la siguiente identidad: \[\begin{equation} y_{i} - \bar{y} = (y_{i} - \widehat{y}_{i}) + (\widehat{y}_{i} - \bar{y}). \tag{1.9} \end{equation}\] La Figura 1.5 muestra la partición (1.9) en el punto \(i=3\). Aquí vemos que una parte de la diferencia entre \(y_{3}\) y \(\bar{y}\) es explicada por el modelo (línea discontinua roja).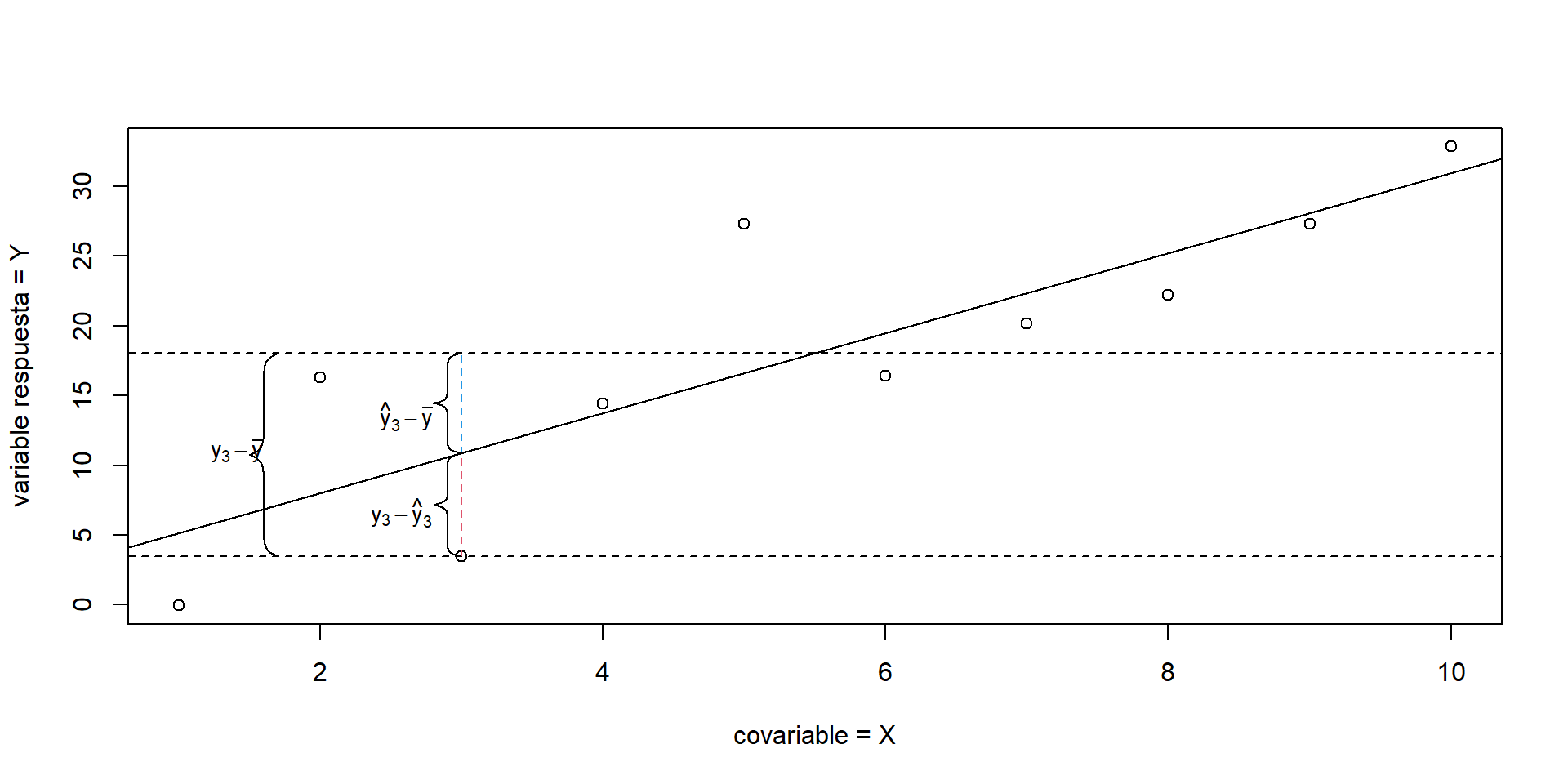

Figure 1.5: Representación gráfica de la descompocisión (1.9).

Ahora elevamos al cuadrado (1.9) y sumamos todos los componentes: \[\begin{equation} \begin{split} SST &= \sum_{i=1}^{n} (y_{i} - \bar{y})^{2} \\ &= \sum_{i=1}^{n} (y_{i} - \widehat{y}_{i})^{2} + \sum_{i=1}^{n}(\widehat{y}_{i} - \bar{y})^{2} + 2 \sum_{i=1}^{n}(y_{i} - \widehat{y}_{i})(\widehat{y}_{i} - \bar{y}) \\ &= \sum_{i=1}^{n} (y_{i} - \widehat{y}_{i})^{2} + \sum_{i=1}^{n}(\widehat{y}_{i} - \bar{y})^{2} \\ SST &= SS_{res} + SS_{R}, \end{split} \tag{1.10} \end{equation}\] donde \(SST\) es llamada la suma de cuadrados totales (con \(n-1\) grados de libertad), \(SS_{R}\) es la suma de cuadrados de la regresión (con \(1\) grados de libertad), y \(SS_{res}\) es la suma de cuadrados residual o del error (con \(n-2\) grados de libertad).

El análisis de varianza nos permite evaluar la siguiente hipótesis: \[\begin{equation} H_{0}: \beta_{1} = 0 \mbox{ }H_{1}: \beta_{1} \neq 0. \tag{1.11} \end{equation}\]

Se puede demostrar que si \(H_{0}\) es cierta: \[ \frac{SS_{res}}{\sigma^{2}} = \frac{(n-2)MS_{res}}{\sigma^{2}} \sim \chi^{2}_{n-2} \mbox{,} \ \ \frac{SS_{R}}{\sigma^{2}} \sim \chi^{2}_{1}, \] y que \(SS_{res}\) y \(SS_{R}\) son independientes. Por lo tanto: \[ F_{0} = \frac{SS_{R}/1}{SS_{res}/(n-2)} = \frac{MS_{R}}{MS_{res}} \sim F_{(1,n-2)}. \] Además, \(E(MS_{res})=\sigma^{2}\) y \(E(MS_{R})=\sigma^{2} + \beta_{1}^{2}S_{xx}\).

Entonces, podemos utilizar \(F_{0}\) como estadístico de prueba de (1.11). Rechazamos \(H_{0}\) si \(F_{0} > F_{\alpha,1,n-2}\).

Si \(H_{0}\) es falsa, \(F_{0}\) sigue una distribución F no central con \(1\) y \(n-2\) grados de libertad, y parámetro de no centralidad igual a \(\lambda=(\beta_{1}^{2}S_{xx})/\sigma^{2}\).

Estos resultados se pueden resumir en la Tabla 1.1.

Table 1.1: Tabla de ANOVA

Fuente de variación	g.l.	SS	MS	\(F\)
regresión	1	\(SS_{R}\)	\(MS_{R}\)	\(F_{0}\)
residuos	n-2	\(SS_{res}\)	\(MS_{res}\)
Total	n-1	\(SST\)

La cantidad: \[ R^{2} = \frac{SS_{R}}{SST} = 1 - \frac{SS_{res}}{SST}, \] es llamada coeficiente de determinación, y cuantifica la cantidad de variabilidad de \(y\) que es explicada por \(x\). Dado que \(0 \leq SS_{res} \leq SST\), se tiene que \(0 \leq R^{2} \leq 1\). Por lo tanto, valores cercanos a \(1\) implican que el modelo explica gran parte de la variabilidad de \(y\).

Datos de grasa corporal. Pruebas de hipótesis y ANOVA

Se quiere probar que la circunferencia del abdomen tiene influencia sobre el % de grasa de los hombres. Esto es: \[ H_{0}: \beta_{1} = 0 \qquad H_{1}: \beta_{1} \neq 0. \] Tanto la prueba de hipótesis basada en \(t_{0}\), el valor \(F_{0}\) del ANOVA, y el \(R^{2}\) se pueden observar usando la función summary:

summary(mod)

## 
## Call:
## lm(formula = brozek ~ abdom, data = fat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -17.6257  -3.4672   0.0111   3.1415  11.9754 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -35.19661    2.46229  -14.29   <2e-16 ***
## abdom         0.58489    0.02643   22.13   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.514 on 250 degrees of freedom
## Multiple R-squared:  0.6621, Adjusted R-squared:  0.6608 
## F-statistic: 489.9 on 1 and 250 DF,  p-value: < 2.2e-16

Del resultado anterior, tenemos que:

• \(t_{0}=22.134\) con un valor-\(p\) asociado de 0. Por lo tanto, rechazamos \(H_{0}\) y concluimos que la circunferencia del abdomen tiene un efecto significativo sobre el % de grasa corporal.

• La función summary no arroja como resultado una tabla ANOVA. Pero podemos observar el valor \(F_{0} = 489.9\) con un valor \(p\) asociado de 0.

• \(R^{2} = 0.662\), lo que indica que el 66.2% de la variabilidad del % de grasa corporal es explicada por la circunferencia del abdomen.

1.6.3 Intervalos de confianza

Intervalos de confianza para \(\beta_{0}\), \(\beta_{1}\) y \(\sigma^{2}\)

Los intervalos de confianza para \(\beta_{0}\) y \(\beta_{1}\) se construyen a partir de las distribuciones de probabilidad de \(\widehat{\beta}_{0}\) y \(\widehat{\beta}_{1}\). Esto es, (1.8) y (1.7), respectivamente.

Por lo tanto, el intervalo del \(100(1-\alpha)\%\) de confianza para \(\beta_{j}\) es: \[ \widehat{\beta}_{j} \pm t_{1-\alpha/2,n-2}\sqrt{V(\widehat{\beta}_{j})}, \mbox{ para }j=0,1. \] Se puede demostrar que \((n-2)MS_{res}/\sigma^{2}\sim \chi^{2}_{n-2}\). Por lo tanto: \[ P \left\{ \chi^{2}_{\alpha/2,n-2} \leq (n-2)MS_{res}/\sigma^{2} \leq \chi^{2}_{1-\alpha/2,n-2} \right\} = 1-\alpha. \] Entonces, el intervalo del \(100(1-\alpha)\%\) de confianza para \(\sigma^{2}\) es: \[ \left\{ \frac{(n-2)MS_{res}}{\chi^{2}_{1-\alpha/2,n-2}}; \frac{(n-2)MS_{res}}{\chi^{2}_{\alpha/2,n-2}} \right\}. \]

Intervalos de confianza para \(E(y_{i})\) y una predicción futura

Cuando el objetivo de ajustar un modelo de regresión es hacer predicciones, es posible hacer intervalos de confianza para la respuesta media, esto es \(E(Y|x_{0})=\mu_{Y|x_{0}}\), donde \(x_{0}\) es un valor de la covariable dentro del rango de valores observados de \(x\) en los datos.

Una estimación insesgada de \(\mu_{Y|x_{0}}\) es: \[ \widehat{\mu}_{Y|x_{0}} = \widehat{\beta}_{0} + \widehat{\beta}_{1}x_{0}. \] La varianza de \(\widehat{\mu}_{Y|x_{0}}\) es: \[\begin{equation} \begin{split} V(\widehat{\mu}_{Y|x_{0}}) &= V(\widehat{\beta}_{0} + \widehat{\beta}_{1}x_{0}) = V(\widehat{\beta}_{0}) + x_{0}^{2}V(\widehat{\beta}_{1}) + 2x_{0}Cov(\widehat{\beta}_{0},\widehat{\beta}_{1}) \\ &= \sigma^{2}\left(\frac{1}{n} + \frac{\bar{x}^{2}}{S_{xx}} \right) + \sigma^{2}x_{0}^{2}\frac{1}{S_{xx}} - 2\sigma^{2}x_{0}\frac{\bar{x}}{S_{xx}} \\ &= \sigma^{2}\left[\frac{1}{n} + \frac{(x_{0}-\bar{x})^{2}}{S_{xx}} \right]. \end{split} \nonumber \end{equation}\] El intervalo de confianza se construye a partir de la siguiente distribución muestral: \[ \frac{\widehat{\mu}_{Y|x_{0}} - E(Y|x_{0})}{\sqrt{MS_{res}[1/n+(x_{0}-\bar{x})^{2}/S_{xx}]}} \sim t_{n-2}. \] Por lo tanto, el intervalo del \(100(1-\alpha)\%\) de confianza para \(\mu_{Y|x_{0}}\) es: \[\begin{equation} \widehat{\mu}_{Y|x_{0}} \pm t_{1-\alpha/2,n-2}\sqrt{MS_{res}[1/n+(x_{0}-\bar{x})^{2}/S_{xx}]}. \label{eq:CImean} \end{equation}\] Note que la longitud del intervalo de confianza de \(\widehat{\mu}_{Y|x_{0}}\) depende del punto \(x_{0}\). La menor longitud se obtiene en el punto \(x_{0}=\bar{x}\), y el intervalo es cada vez mas ancho a medida que nos alejamos de ese punto.

Ahora consideremos hacer una predicción de una observación futura de \(y\) para cierto valor de \(x\). Si queremos hacer la predicción para \(x=x_{0}\), entonces la predicción de la nueva observación es: \[ \widetilde{y}_{0} = \widehat{\beta}_{0} + \widehat{\beta}_{1}x_{0}. \] Asumiendo que el modelo es correcta, el verdadero valor de \(y_{0}\) es: \[ \widetilde{y}_{0} = \widehat{\beta}_{0} + \widehat{\beta}_{1}x_{0} + \varepsilon_{0}. \] y su varianza es: \[\begin{equation} V(\widetilde{y}_{0}) = \sigma^{2}+\sigma^{2}\left[\frac{1}{n} + \frac{(x_{0}-\bar{x})^{2}}{S_{xx}} \right]. \tag{1.12} \end{equation}\] El primer término a la derecha de (1.12) corresponde a la variabilidad de \(\varepsilon_{0}\) y el segundo al error de estimación de los coeficientes \(\beta_{0}\) y \(\beta_{1}\). A partir de estos resultados, el intervalo del \(100(1-\alpha)\%\) de predicción de una observación futura en \(x=x_{0}\) es: \[ \widehat{\mu}_{Y|x_{0}} \pm t_{1-\alpha/2,n-2}\sqrt{MS_{res}[1+1/n+(x_{0}-\bar{x})^{2}/S_{xx}]}. \]

Datos de grasa corporal. Intervalos de confianza

El intervalo del 95% de confianza para los parámetros del modelo (1.4) son:

confint(mod)

##                  2.5 %      97.5 %
## (Intercept) -40.046092 -30.3471234
## abdom         0.532846   0.6369351

Para \(\beta_{1}\), con un nivel de confianza del 95% podemos decir que la diferencia promedio en el % de grasa, comparando dos hombres con una diferencia de un centímetro en la circunferencia del abdomen, está entre 0.53% y 0.64% con un nivel de confianza del 95%. Como mencionamos antes, \(\beta_{0}\) no tiene interpretación en este modelo.

El intervalo del 95% de confianza para \(\sigma\) se calcula “a pie” de la siguiente forma:

var.limInf = sum(mod$residuals^2)/qchisq(0.975,df=mod$df.residual)
var.limSup = sum(mod$residuals^2)/qchisq(0.025,df=mod$df.residual)
sqrt(c(var.limInf,var.limSup))

## [1] 4.150992 4.948065

Se quiere estimar el % de grasa corporal medio de los hombres que tiene una circunferencia del abdomen de 80cm. Entonces, la estimación puntual es: \[ \widehat{\mu}_{\mbox{brozek}|\mbox{abdom}=80} = \widehat{\beta}_{0} + \widehat{\beta}_{1}(80) = -35.197 + 0.585*80 = 11.603. \] El intervalo del 95% de confianza para esta estimación se puede calcular de la siguiente forma:

x.nuevo = data.frame(abdom=80)
pred.media = predict(mod,x.nuevo,interval = 'confidence')
pred.media

##        fit      lwr      upr
## 1 11.59463 10.73398 12.45528

Esto quiere decir que, con un nivel de confianza del 95%, el % de grasa corporal medio de los hombres que tienen una circunferencia del abdomen de 80cm está entre 10.73 y 12.46 por ciento.

Ahora, suponga que se quiere predecir el % de grasa corporal de un hombre que tiene una circunferencia del abdomen de 100cm. Para esto debemos calcular un intervalo de predicción del 95%:

x.nuevo = data.frame(abdom=100)
pred.nuevaObs = predict(mod,x.nuevo,interval = 'prediction')
pred.nuevaObs

##        fit      lwr      upr
## 1 23.29244 14.37532 32.20957

Por lo tanto, con un nivel de confianza del 95% el % de grasa de este hombre está entre 14.38 y 32.21 por ciento.

Gráficamente, podemos ver los intervalos de confianza y predicción de la siguiente forma. Primero, hacemos la predicciones para edades gestacionales entre 33 y 45 semanas:

x.nuevo = data.frame(abdom=seq(from=69,to=149,length.out = 100))
pred.media = predict(mod,x.nuevo,interval = 'confidence')
pred.nuevaObs = predict(mod,x.nuevo,interval = 'prediction')

Luego hacemos el gráfico:

plot(brozek~abdom,data=fat,pch=20,xlab="circunferencia del abdomen(cm)",
     ylab='% de grasa corporal')
abline(mod)
lines(x.nuevo$abdom,pred.media[,2],lty=2)
lines(x.nuevo$abdom,pred.media[,3],lty=2)
lines(x.nuevo$abdom,pred.nuevaObs[,2],lty=3)
lines(x.nuevo$abdom,pred.nuevaObs[,3],lty=3)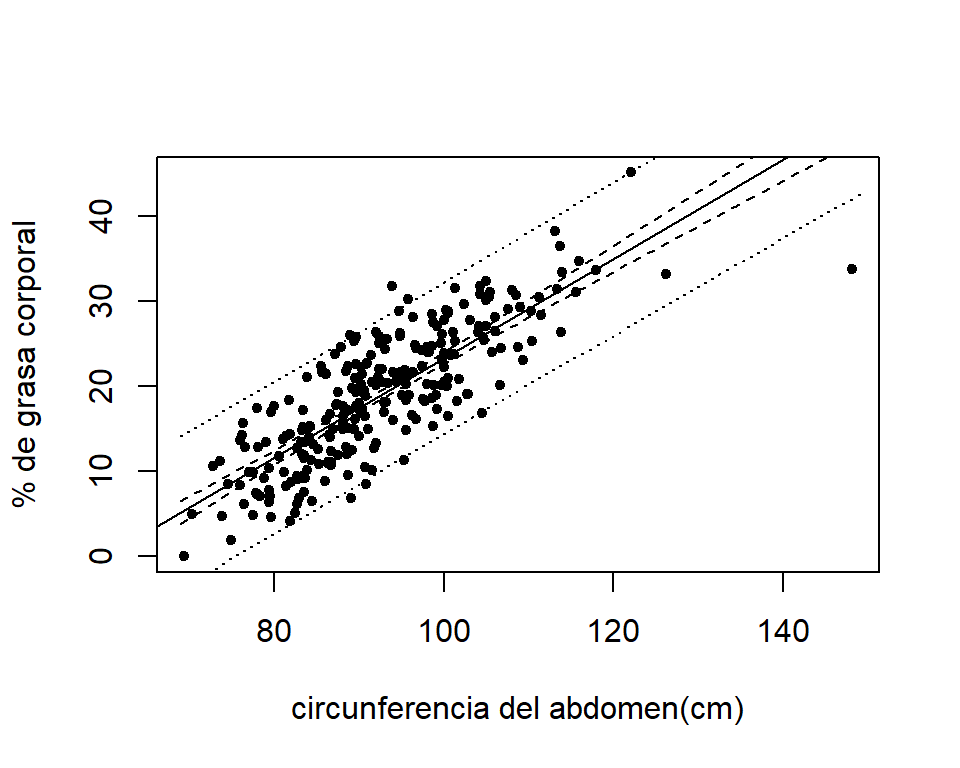

Figure 1.6: Intervalos del 95% de confianza (línea discontinua) y predicción (línea punteada) para el % de grasa corporal en función de la circunferencia del abodmen.

1.7 Estimador por máxima verosimilitud

Si consideramos que \(\varepsilon_{i}\sim N(0,\sigma^{2})\), entonces las observación también se distribuyen de forma normal \(y_{i}\sim N(\beta_{0}+\beta_{1}x_{i},\sigma^{2})\). Si además asumimos que las observaciones \((y_{i},x_{i})\) son independientes, entonces la función de verosimilitud es: \[\begin{equation} \begin{split} L(\boldsymbol \theta) =& \prod_{i=1}^{n} \left(\sqrt{2\pi\sigma^{2}} \right)^{-1/2}\exp\left[ - \frac{1}{2\sigma^{2}}(y_{i}-\beta_{0}-\beta_{1}x_{i})^{2} \right] \\ =& \left( \sqrt{2\pi\sigma^{2}} \right)^{-n/2}\exp\left[ - \frac{1}{2\sigma^{2}} \sum_{i=1}^{n}(y_{i}-\beta_{0}-\beta_{1}x_{i})^{2}\right], \end{split} \nonumber \end{equation}\] para \(\boldsymbol \theta=(\beta_{0},\beta_{1},\sigma^{2})'\). La log-verosimilitud es: \[ \ell (\boldsymbol \theta) = - \left(\frac{n}{2}\right)\left[ \log (2 \pi) - \log \sigma^{2}\right] - \frac{1}{2\sigma^{2}}\sum_{i=1}^{n}(y_{i} - \beta_{0}-\beta_{1}x_{i})^{2}. \] El estimador de máxima verosimilitud de \(\boldsymbol \theta\) debe satisfacer: \[ \left. \frac{\partial \ell(\boldsymbol \theta)}{\partial \beta_{0}} \right|_{\widetilde{\boldsymbol \theta}} = \frac{1}{\widetilde{\sigma}^{2}}\sum_{i=1}^{n}(y_{i} - \beta_{0}-\beta_{1}x_{i}) = 0, \] \[ \left. \frac{\partial \ell(\boldsymbol \theta)}{\partial \beta_{1}} \right|_{\widetilde{\boldsymbol \theta}} = \frac{1}{\widetilde{\sigma}^{2}}\sum_{i=1}^{n}(y_{i} - \beta_{0}-\beta_{1}x_{i})x_{i} = 0, \] y \[ \left. \frac{\partial \ell(\boldsymbol \theta)}{\partial \sigma^{2}} \right|_{\widetilde{\boldsymbol \theta}} = -\frac{n}{2\widetilde{\sigma}^{2}} + \frac{n}{2\widetilde{\sigma}^{4}} \sum_{i=1}^{n}(y_{i} - \beta_{0}-\beta_{1}x_{i})^{2} = 0, \] Luego de solucionar las ecuaciones anteriores se obtienen los estimadores por máxima verosimilitud: \[ \widetilde{\beta}_{0} = \bar{y} - \widetilde{\beta}_{1}\bar{x}, \] \[ \widetilde{\beta}_{1} = \frac{\sum_{i=1}^{n}y_{i}(x_{i}-\bar{x})}{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}, \] y \[ \widetilde{\sigma}^{2} = \frac{\sum_{i=1}^{n}(y_{i}-\beta_{0}-\beta_{1}x_{i})^{2}}{n}. \] Aquí observamos que los estimadores por máxima verosimilitud para \(\beta_{0}\) y \(\beta_{1}\) son equivalente a los estimadores por MCO. El estimador de \(\sigma^{2}\) es sesgado, sin embargo el sesgo disminuye a medida que \(n\) crece.

Por lo general, los estimadores por máxima verosimilitud tienen mejores propiedades que los estimadores por MCO. Son asintoticamente insesgados, consistentes y asintoticamente de mínima varianza. Sin embargo, estos requieren de supuestos distribucionales completos. Recordemos que los estimadores por MCO solo requieren de una correcta especificación de los dos primeros momentos (valor esperado, varianza y covarianza).

1.8 Algunas consideraciones finales

• Las conclusiones sobre los modelos de regresión se hacen sobre el rango de valores observados de las covariables (interpolación). Por ejemplo, en los datos de grasa corporal, se pueden hacer inferencias sobre el peso al nacer para bebés que nacen en entre las semanas 69.4 y 148.1. Cuando hacemos estimaciones fuera de este rango estaríamos extrapolando.

Por extrapolación nos referimos a hacer predicciones fuera del rango observado de \(x\). La Figura 1.7 muestra el problema que se puede cometer cuando extrapolamos. Si tenemos datos en el rango \(x_{min} \leq x \leq x_{max}\), un modelo lineal es una buena aproximación de \(E(Y|x)\). Pero, esa aproximación no es buena para \(x>x_{max}\). Por lo tanto, se estaría cometiendo errores graves cuando hacemos predicciones de \(Y\) para valores de \(x\) mayores a \(x_{max}\) (por ejemplo en el punto \(x_{0}\)).

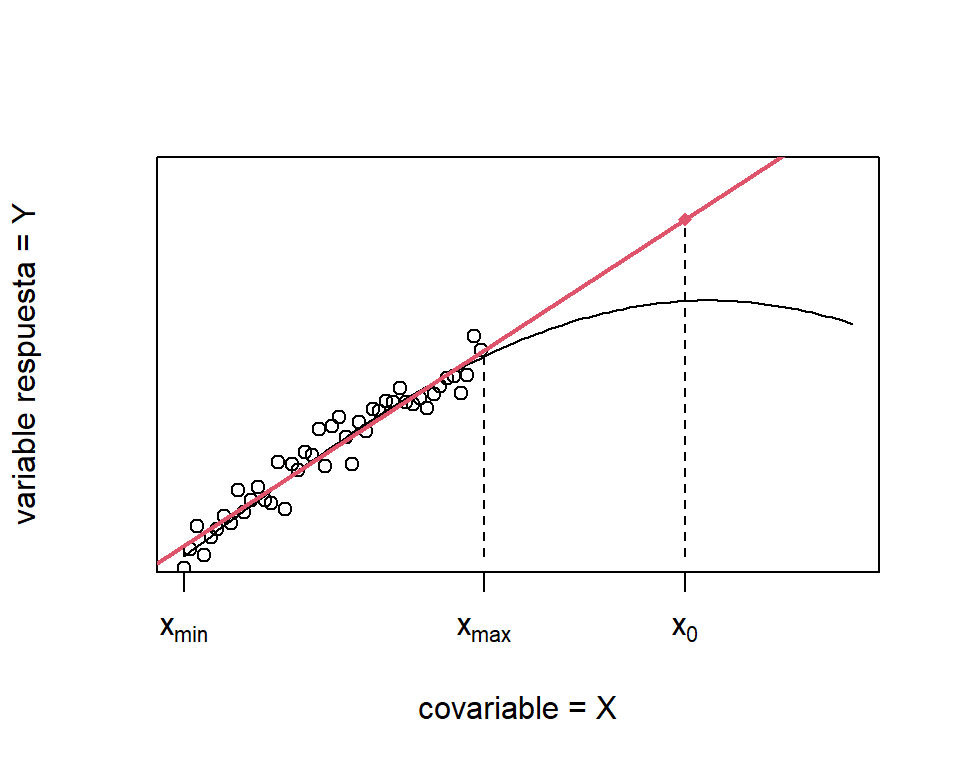
Figure 1.7: Peligro de extrapolar. La curva negra representa \(E(Y|x)\) y la línea roja es el ajuste del modelo lineal con los datos observados de \(x\). La predicción en el punto \(x_{0}\) es bastante sesgada.

• La posición de los valores de \(x\) tienen una influencia sobre el ajuste por MCO. Particularmente, la estimación de \(\beta_{1}\) está fuertemente influenciada por los valores alejados de \(x\) y \(y\). A estos puntos se les denomina puntos influyentes. En la Figura 1.8(a) podemos ver como un solo punto tiene una influencia alta en la estimación de los parámetros del modelo.

• Los valores atípicos son observaciones que difieren considerablemente del resto de los datos (generalmente en \(y\)). Un punto atípico puede afectar la estimación de \(\beta_{0}\) (ver Figura 1.8(b) y la estimación de \(\sigma^{2}\).

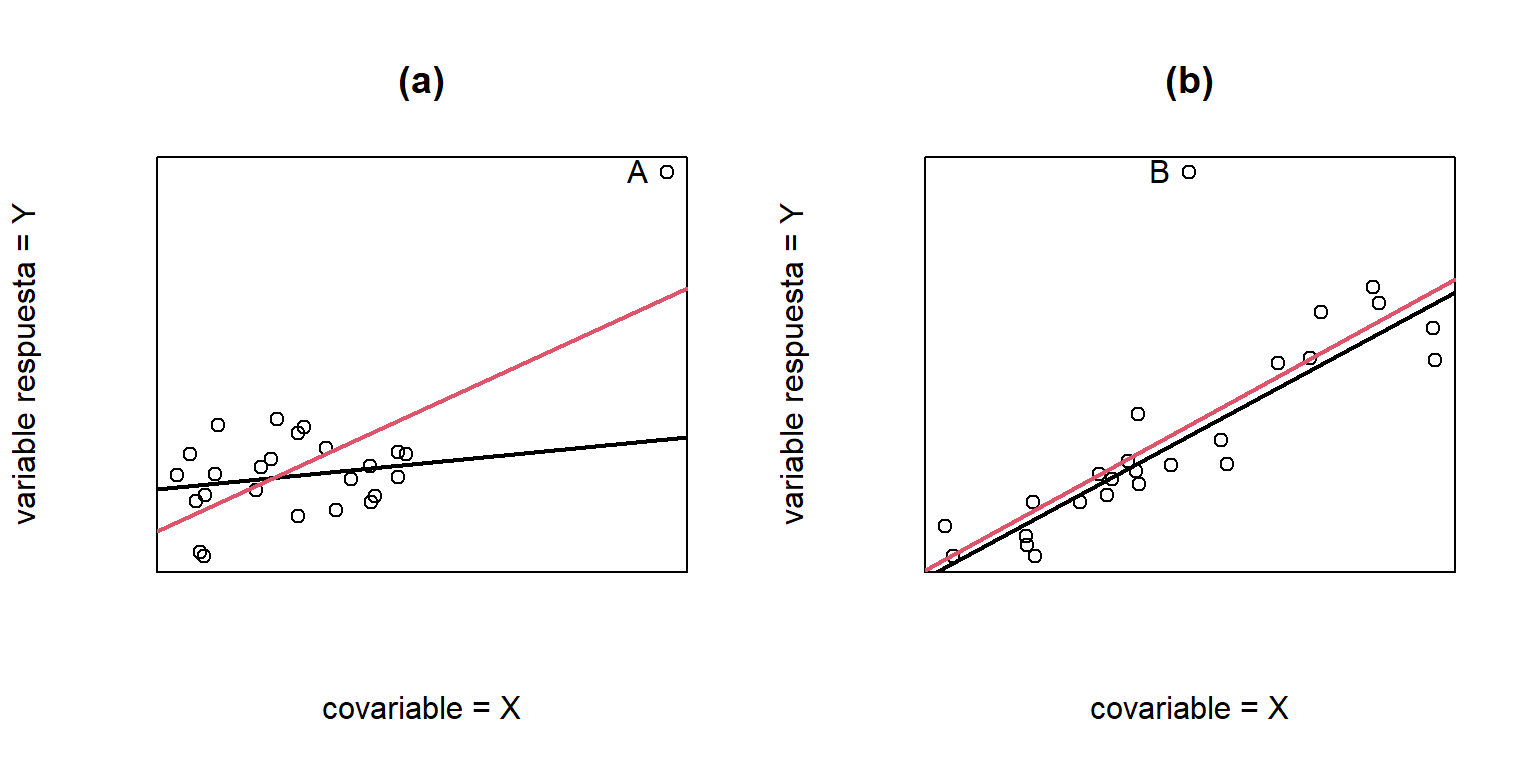
Figure 1.8: (a) Efecto de un punto influyente, la línea negra es la estimación sin el punto A y la linea roja es la estimación incluyento el punto A. (b) Efecto de un punto atípico, la línea negra es la estimación sin el punto B y la linea roja es la estimación incluyento el punto B.

Los métodos para la detección de puntos atípicos e influyentes se presentarán en un capítulo posterior.

• Una fuerte relación entre dos variables no necesariamente implica que la relación entre las variables es de causa-efecto. Un modelo de regresión nos permite modelar variables que estén correlacionadas, pero no se puede concluir que, necesariamente, es una relación causal.

References

Montgomery, Douglas C., Elizabeth A. Peck, and G. Geoffrey Vining. 2012. Introduction to Linear Regression Analysis. 5th ed. Wiley.