Capítulo 2 Modelo lineal múltiple

Bajo peso al nacer

Retomemos la base de datos de bajo peso al nacer. Aparte de la edad gestacional, el peso del recién nacido puede estar explicado con otros factores. Por ejemplo, el peso de los padres, salud de la madre, entre otros. A parte de la edad gestacional y el peso del recién nacido, vamos a observar también la variable peso de la madre antes del embarazo.

La Figura 2.1 muestra la relación entre las variables de estudio. Aquí podemos observar una relación lineal positiva fuerte entre el peso al nacer y la edad gestacional (correlación igual a 0.73). La relación entre el peso al nacer y el peso de la madre es lineal positiva, aunque no tan fuerte como la anterior (correlación igual a 0.3).

La Figura 2.1 y la matriz de correlación se pueden hacer con los siguientes códigos:

birthweight = read.csv("birthweight.csv",header = T)
pairs(birthweight[,c(3,4,8)])

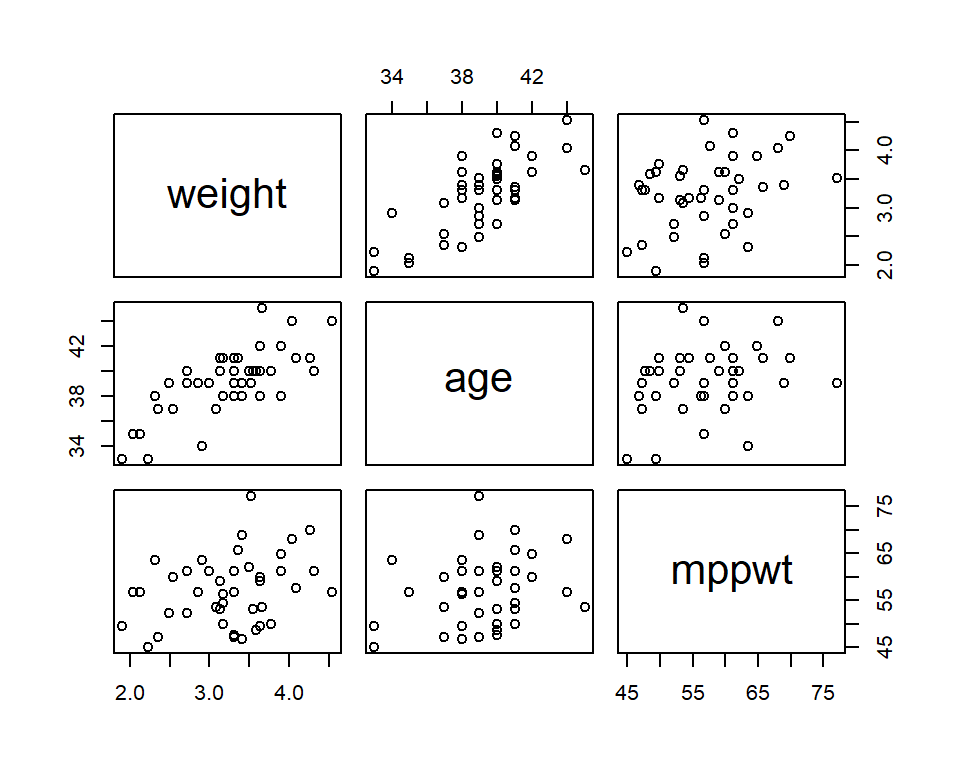
Figure 2.1: Gráfico de dispersion del peso del recien nacido y la edad gestacional.

cor(birthweight[,c(3,4,8)])

##           weight       age     mppwt
## weight 1.0000000 0.7311334 0.3048027
## age    0.7311334 1.0000000 0.2505155
## mppwt  0.3048027 0.2505155 1.0000000

Por lo tanto, junto con la edad gestacional, ahora vamos a incluir peso de la madre antes del embarazo (en kgs, mppwt) como covariable. Por lo tanto, el modelo propuesto es: \[ \mbox{weight}_{i} = \beta_{0} + \beta_{1}\mbox{age}_{i} + \beta_{2}\mbox{mppwt}_{i} + \varepsilon_{i}, \mbox{ para }i=1,\ldots,42, \] con \(\varepsilon_{i}\sim N(0,\sigma^{2})\), y \(cov(\varepsilon_{j},\varepsilon_{k})=0\) para todo \(j\neq k\).

2.1 Modelo lineal múltiple

En general, se puede relacionar la variable respuesta (\(y\)), con \(p-1\) covariables (o variables predictoras). El modelo lineal múltiple se expresa de la siguiente forma:

\[\begin{equation} \begin{split} y_{i} =& \beta_{0} + \beta_{1}x_{i1} + \beta_{2}x_{i2} + \ldots + \beta_{p-1} x_{i,p-1} + \varepsilon_{i} \\ =& \boldsymbol x_{i}'\boldsymbol \beta+ \varepsilon_{i}, \qquad i=1,\ldots,n, \\ \end{split} \tag{2.1} \end{equation}\]

donde \(\boldsymbol x_{i} = (1,x_{i1},x_{i2},\ldots,x_{i,p-1})'\) es el vector de dimensión \(p\) de covariables del individuo \(i\) y \(\boldsymbol \beta= (\beta_{0},\beta_{1},\ldots,\beta_{p-1})'\) es el vector de dimensión \(p\) de coeficientes de regresión.

Los supuestos del modelo son los mismos que se plantearon en el capítulo anterior. Estos es: \(\varepsilon_{i} \sim N\left(0,\sigma^{2} \right)\) y \(cov(\varepsilon_{j},\varepsilon_{k})=0\), para todo \(j \neq k\).

Dado que \(E(\varepsilon_{i})=0\), el valor esperado de \(Y\) es: \[\begin{equation} E(Y| x_{i1},x_{i2},\ldots,x_{i,p-1}) = E(Y| \boldsymbol x_{i}) = \beta_{0} + \beta_{1}x_{i1} + \beta_{2}x_{i2} + \ldots + \beta_{p-1} x_{i,p-1} = \boldsymbol x_{i}'\boldsymbol \beta. \tag{2.2} \end{equation}\] El intercepto \(\beta_{0}\) es el valor esperado de \(Y\) cuando \(x_{i}=(1,0,0,\ldots,0)'\), es decir cuando todos las covariables toman el valor \(0\).

El parámetro de pendiente \(\beta_{j}\) indica el cambio en el valor esperado de \(Y\) debido a un aumento unitario en la covariable \(x_{j}\) cuando todas las demás variables predictoras se mantienen constantes. Sean \(x_{i,j} = (1,x_{i1},\ldots,x_{ij},\ldots,x_{i,p-1})\) y \(x_{i,j+1} = (1,x_{i1},\ldots,x_{ij}+1,\ldots,x_{i,p-1})\). A partir de (2.2), tenemos: \[ E(Y|x_{i,j}) = \beta_{0} + \beta_{1}x_{i1} + \ldots + \beta_{j}x_{ij} + \ldots + \beta_{p-1} x_{i,p-1}, \] y \[ E(Y|x_{i,j+1}) = \beta_{0} + \beta_{1}x_{i1} + \ldots + \beta_{j}(x_{ij}+1) + \ldots + \beta_{p-1} x_{i,p-1}. \] De aquí tenemos que: \[ E(Y|x_{i,j+1}) - E(Y|x_{i,j}) = \beta_{j}. \] Es conveniente escribir el modelo de regresión múltiple (2.1) de forma matricial: \[ \boldsymbol y= \boldsymbol X\boldsymbol \beta+ \boldsymbol \varepsilon, \] donde: \[\begin{gather} \begin{aligned} \boldsymbol y= \begin{pmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{pmatrix}, & \boldsymbol X= \begin{pmatrix} 1 & x_{11} & x_{12} & \ldots & x_{1,p-1} \\ 1 & x_{21} & x_{22} & \ldots & x_{2,p-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \ldots & x_{n,p-1} \end{pmatrix}, \boldsymbol \beta= \begin{pmatrix} \beta_{0} \\ \beta_{1} \\ \beta_{2} \\ \vdots \\ \beta_{p-1} \end{pmatrix}, & \boldsymbol \varepsilon= \begin{pmatrix} \varepsilon_{1} \\ \varepsilon_{2} \\ \vdots \\ \varepsilon_{n} \end{pmatrix}. \end{aligned} \nonumber \end{gather}\] Además, los supuestos sobre los errores se pueden expresar como \(\boldsymbol \varepsilon\sim N(\boldsymbol 0, \sigma^{2}\boldsymbol I)\), donde \(\boldsymbol 0\) es un vector con todas las entradas iguales a cero, y \(\boldsymbol I\) es la matriz identidad.

2.2 Estimación de los parámetros de regresión

La estimación de \(\boldsymbol \beta\) se hace a través del método de mínimos cuadrados ordinarios. Por lo tanto, debemos encontrar el vector \(\widehat{\boldsymbol \beta}\) que minimice: \[ S(\boldsymbol \beta) = \sum_{i=1}^{n}\left(y_{i} - \boldsymbol x_{i}'\boldsymbol \beta\right)^2 = \sum_{i=1}^{n}e_{i}^2. \] En forma matricial, tenemos: \[\begin{equation} \begin{split} S(\boldsymbol \beta) &= \boldsymbol e'\boldsymbol e= (\boldsymbol y- \boldsymbol X\boldsymbol \beta)'(\boldsymbol y- \boldsymbol X\boldsymbol \beta) \\ &= \boldsymbol y'\boldsymbol y- \boldsymbol \beta'\boldsymbol X'\boldsymbol y- \boldsymbol y'\boldsymbol X\boldsymbol \beta+ \boldsymbol \beta'\boldsymbol X'\boldsymbol X\boldsymbol \beta\\ &= \boldsymbol y'\boldsymbol y- 2\boldsymbol \beta'\boldsymbol X'\boldsymbol y+ \boldsymbol \beta'\boldsymbol X'\boldsymbol X\boldsymbol \beta. \end{split} \nonumber \end{equation}\] Por lo tanto, \(\widehat{\boldsymbol \beta}\) debe satisfacer: \[ \left. \frac{\partial S}{\partial \boldsymbol \beta} \right|_{\widehat{\boldsymbol \beta}} = - 2\boldsymbol X'\boldsymbol y+ 2\boldsymbol X'\boldsymbol X\widehat{\boldsymbol \beta}= \boldsymbol 0. \] A partir de aquí obtenemos las ecuaciones normales: \[ \boldsymbol X'\boldsymbol X\widehat{\boldsymbol \beta}= \boldsymbol X'\boldsymbol y. \] En más detalle: \[\begin{gather} \begin{pmatrix} n & \sum x_{i1} & \sum_{i=1}^{n}x_{i2} & \ldots & \sum_{i=1}^{n}x_{i,p-1} \\ \sum x_{i1} & \sum x_{i1}^2 & \sum x_{i1}x_{i2} & \ldots & \sum x_{i1}x_{i,p-1} \\ \sum x_{i2} & \sum x_{i1}x_{i2} & \sum x_{i2}^2 & \ldots & \sum x_{i2}x_{i,p-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \sum x_{i,p-1} & \sum x_{i1}x_{i,p-1} & \sum x_{i2}x_{i,p-1} & \ldots & \sum x_{i,p-1}^{2} \\ \end{pmatrix} \begin{pmatrix} \widehat{\beta}_{0} \\ \widehat{\beta}_{1} \\ \vdots \\ \widehat{\beta}_{p-1} \end{pmatrix} = \begin{pmatrix} \sum y_{i} \\ \sum x_{i1}y_{i} \\ \vdots \\ \sum x_{i,p-1}y_{i} \end{pmatrix} \nonumber \end{gather}\] Por lo cual, el estimador por mínimos cuadrados es: \[ \widehat{\boldsymbol \beta}= (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y. \] Note que es necesario que \(\boldsymbol X\) sea de rango completo, \(\mbox{rango}(\boldsymbol X) = p \leq n\). Esta restricción es necesaria para asegurar que \(\boldsymbol X'\boldsymbol X\) sea no singular. Si \(\boldsymbol X'\boldsymbol X\) es singular, implica que existe una combinación lineal entre las columnas de \(\boldsymbol X\), o que \(\mbox{rango}(\boldsymbol X) < p\).

El valor ajustado de \(y\) para el vector de covariables \(\boldsymbol x_{i}\) es \(\widehat{y}_{i}= \boldsymbol x_{i}'\widehat{\boldsymbol \beta}\). Definiendo \(\widehat{\boldsymbol y}= (\widehat{y}_{1},\widehat{y}_{2},\ldots,\widehat{y}_{n})\), tenemos que: \[ \widehat{\boldsymbol y}= \boldsymbol X\widehat{\boldsymbol \beta}= \boldsymbol X(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y= \boldsymbol H\boldsymbol y. \] La matriz \(\boldsymbol H= \boldsymbol X(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\) es llamada matriz hat (sombrero) y desempeña un papel importante en el análisis de regresión.

Los residuos del modelo \((e_{i}=y_{i}-\widehat{y}_{i})\) también se pueden expresar en forma matricial como: \[ \boldsymbol e= \boldsymbol y- \boldsymbol X'\widehat{\boldsymbol \beta}= \boldsymbol y- \boldsymbol X(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y= \boldsymbol y- \boldsymbol H\boldsymbol y= (\boldsymbol I_{n} - \boldsymbol H)\boldsymbol y. \]

2.2.1 Estimación de \(\sigma^{2}\)

Al igual que en la regresión simple, el estimador de \(\sigma^{2}\) es el cuadrado medio del error, definido como: \[ MS_{res} = \frac{SS_{res}}{n-p}, \] donde: \[\begin{equation} \begin{split} SS_{res} &= \sum_{i=1}^{n}e^{2}_{i} = \boldsymbol e'\boldsymbol e= (\boldsymbol y- \boldsymbol X\widehat{\boldsymbol \beta})'(\boldsymbol y- \boldsymbol X\widehat{\boldsymbol \beta}) \\ &= (\boldsymbol y- \boldsymbol H\boldsymbol y)'(\boldsymbol y- \boldsymbol H\boldsymbol y) = \boldsymbol y'(\boldsymbol I_{n}-\boldsymbol H)'(\boldsymbol I_{n}-\boldsymbol H)\boldsymbol y= \boldsymbol y'(\boldsymbol I_{n} - \boldsymbol H)\boldsymbol y. \end{split} \nonumber \end{equation}\] Se puede demostrar que \(MS_{res}\) es un estimador insesgado de \(\sigma^{2}\), es decir \(E(MS_{res})=\sigma^{2}\). Para esto debemos calcular el valor esperado de \(SS_{res}\).

Sabemos que \(E(\boldsymbol y) = \boldsymbol X\boldsymbol \beta\) y \(V(\boldsymbol y) = \sigma^{2}\boldsymbol I_{n}\), entonces: \[ E(SS_{res}) = E\left[\boldsymbol y'(\boldsymbol I_{n} - \boldsymbol H)\boldsymbol y\right] = \sigma^{2}\mbox{tr}\left( \boldsymbol I_{n} - \boldsymbol H\right) + \boldsymbol \beta'\boldsymbol X'(\boldsymbol I_{n} - \boldsymbol H)\boldsymbol X\boldsymbol \beta= (n-p)\sigma^{2}. \] Por lo tanto, \(E(MS_{res}) = E(SS_{res})/(n-p) = \sigma^{2}\).

2.2.2 Bajo peso al nacer - estimación de parámetros

Para ajustar el modelo: \[ \mbox{weight}_{i} = \beta_{0} + \beta_{1}\mbox{age}_{i} + \beta_{2}\mbox{mppwt}_{i} + \varepsilon_{i}, \mbox{ para }i=1,\ldots,42, \] con \(\varepsilon_{i}\sim N(0,\sigma^{2})\), y \(cov(\varepsilon_{j},\varepsilon_{k})=0\) para todo \(j\neq k\), usamos la función lm de R:

mod = lm(weight ~ age + mppwt, data=birthweight)
mod

## 
## Call:
## lm(formula = weight ~ age + mppwt, data = birthweight)
## 
## Coefficients:
## (Intercept)          age        mppwt  
##    -3.97750      0.16746      0.01142

De aquí temenos que: \[ E(\mbox{weight} | \mbox{age}, \mbox{mppwt})= -3.978+0.167\mbox{age}+0.011\mbox{mppwt}. \] Aquí vemos que ambas covariables tienen un efecto positivo sobre el peso del bebé al nacer. Especificamente, tenemos que:

• Si la edad gestacional aumenta en una semana y el peso de la madre se mantiene constante, el valor esperado del peso al nacer crece 167 gramos.
• Por cada incremento de un kilogramo en el peso de la madre y manteniendo la edad gestacional constante, el peso al nacer medio aumenta 11 gramos.

Además, la estimación de \(\sigma^{2}\) es:

 sqrt(sum(mod$residuals^2)/39)

## [1] 0.4356247

Note que al adicionar la covariable mppwt se redujo el \(MS_{res}\).

2.2.3 Propiedades de los estimadores por MCO

El valor esperado de \(\widehat{\boldsymbol \beta}\) es: \[\begin{equation} \begin{split} E(\widehat{\boldsymbol \beta}) =& E\left[ (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y\right] = E\left[ \boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'(\boldsymbol X\boldsymbol \beta+ \boldsymbol \varepsilon) \right] \\ =& E\left[ (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol X\boldsymbol \beta+ (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol \varepsilon\right] = \boldsymbol \beta \end{split} \nonumber \end{equation}\] Por lo tanto, \(\widehat{\boldsymbol \beta}\) es un estimador insesgado de \(\boldsymbol \beta\) (si el modelo está bien espeficado).

La matriz de varianzas-covarianzas de \(\widehat{\boldsymbol \beta}\) es: \[\begin{equation} \begin{split} V(\widehat{\boldsymbol \beta}) &= V\left[ (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y\right] = (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'V(\boldsymbol y)\boldsymbol X(\boldsymbol X'\boldsymbol X)^{-1} \\ &= \sigma^{2}(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol X(\boldsymbol X'\boldsymbol X)^{-1} = \sigma^{2}(\boldsymbol X'\boldsymbol X)^{-1}. \end{split} \nonumber \end{equation}\] Si \(\boldsymbol C=(\boldsymbol X'\boldsymbol X)^{-1}\), entonces \(V(\widehat{\beta}_{j}) = \sigma^{2}c_{jj}\) y \(Cov(\widehat{\beta}_{j},\widehat{\beta}_{k})=\sigma^{2}c_{jk}\), donde \(c_{jk}\) es la entrada \((j,k)\) de la matriz \(\boldsymbol C\).

Teorema de Gauss-Markov

Si, \(E(\boldsymbol \varepsilon) = \boldsymbol 0\) y \(V(\boldsymbol \varepsilon) = \sigma^{2}\boldsymbol I_{n}\), el estimador por MCO, \(\widehat{\boldsymbol \beta}= (\boldsymbol X'\boldsymbol X)\boldsymbol X'\boldsymbol y\), es el mejor estimador lineal insesgado de \(\boldsymbol \beta\). Esto quiere decir que es el estimador con menor varianza entre la clase de estimador insesgados que son combinaciones lineales de \(y\). Para la demostración, ver Sección C4 de Montgomery, Peck, and Vining (2012).

Además, si \(\boldsymbol \varepsilon\sim N(\boldsymbol 0, \sigma^{2}\boldsymbol I_{n})\), el estimador por MCO coincide con el estimador por máxima verosimilitud.

2.3 Pruebas de hipótesis

Después de estimar el modelo podemos preguntarnos:

• ¿el modelo hace un buen ajuste de los datos?
• ¿cuales regresores específicos parecen importantes?

Para resolver estas preguntas podemos realizar pruebas de hipótesis. Generalmente, estos test requieren que \(\boldsymbol \varepsilon\sim N(\boldsymbol 0,\sigma^{2}\boldsymbol I_{n})\).

2.3.1 Análisis de varianza

Para probar la significancia del modelo (determinar si que la relación entre \(y\) y algunas de las covariables es lineal) se plantean las siguientes hipótesis: \[\begin{equation} \begin{split} H_{0}:& \beta_{1}=\beta_{2}=\ldots=\beta_{p-1} = 0 \\ H_{1}:& \beta_{j}\neq 0 \mbox{ para al menos un }j. \end{split} \tag{2.3} \end{equation}\] El rechazo de esta hipótesis nula implica que al menos uno de los regresores \(x_1, x_2,\ldots , x_{p-1}\) contribuye significativamente al modelo.

Igual que en la regresión simple, el estadístico de prueba se encuentra a partir de la partición de la suma de cuadrados totales: \[ SS_{T} = SS_{R} + SS_{res}, \] donde:

• \(SS_{R} = \sum_{i=1}^{n}(\widehat{y}_{i}-\bar{y})^{2} = (\boldsymbol H\boldsymbol y- \frac{1}{n}\boldsymbol 1\boldsymbol 1'\boldsymbol y)'(\boldsymbol H\boldsymbol y- \frac{1}{n}\boldsymbol 1\boldsymbol 1'\boldsymbol y)=\boldsymbol y'(\boldsymbol H- \frac{1}{n}\boldsymbol 1\boldsymbol 1')\boldsymbol y\),
• \(SS_{res} = \sum_{i=1}^{n}(y_{i}-\widehat{y}_{i})^{2} = (\boldsymbol y- \boldsymbol H\boldsymbol y)'(\boldsymbol y- \boldsymbol H\boldsymbol y)=\boldsymbol y'(\boldsymbol I_n-\boldsymbol H)\boldsymbol y\),

y \(\boldsymbol 1\) es un vector cuyas entradas son iguales a \(1\).

Se tiene que, \(\frac{SS_{R}}{\sigma^2} \sim \chi^2_{r,\lambda}\), con: \[\begin{equation} \lambda = \frac{\boldsymbol \beta^{*'}\boldsymbol X_{c}'\boldsymbol X_{c}\boldsymbol \beta^{*}}{\sigma^{2}}, \tag{2.4} \end{equation}\] donde donde \(\boldsymbol \beta^{*} = (\beta_{1},\beta_{2},\ldots,\beta_{p-1})'\) y \[ \boldsymbol X_{c} = \begin{pmatrix} x_{11} - \bar{x}_{1} & x_{12} - \bar{x}_{2} & \ldots & x_{1,p-1} - \bar{x}_{p-1} \\ x_{21} - \bar{x}_{1} & x_{22} - \bar{x}_{2} & \ldots & x_{2,p-1} - \bar{x}_{p-1} \\ \vdots & \vdots & \ddots & \vdots \\ x_{i1} - \bar{x}_{1} & x_{i2} - \bar{x}_{2} & \ldots & x_{i,p-1} - \bar{x}_{p-1} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} - \bar{x}_{1} & x_{n2} - \bar{x}_{2} & \ldots & x_{n,p-1} - \bar{x}_{p-1} \\ \end{pmatrix}. \] De igual forma, \(\frac{SS_{res}}{\sigma^2} \sim \chi^2_{n-p}\). Finalmente, se puede probar que \(SS_{R}\) y \(SS_{res}\) son independientes.

Si \(H_{0}\) es cierta, tenemos que: \[ \frac{SS_{res}}{\sigma^{2}}\sim\chi^{2}_{n-p} \mbox{ y } \frac{SS_{R}}{\sigma^{2}} \sim \chi^{2}_{p-1}. \] Por lo tanto, \[ F_{0} = \frac{SS_{R}/(p-1)}{SS_{res}/(n-p)} = \frac{MS_{R}}{MS_{res}} \sim F_{p-1,n-p}. \]

Si \(H_{0}\) no es cierta, tenemos que \(F_{0}\) sigue una distribución \(F\) no-central con \(p-1\) y \(n-p\) grados de libertad y parámetro de no centralidad (2.4).

Estos nos resultados nos indican que si el valor \(F_{0}\) es grande, entonces al menos un \(\beta_{j}\) es diferente de cero.

Por lo tanto, para probar las hipótesis (2.3) calculamos el estadístico de prueba \(F_{0} = \frac{MS_{R}}{MS_{res}}\), y rechazamos \(H_{0}\) si \(F_{0} > F_{1-\alpha,p-1,n-p}\).

A partir de las sumas de cuadrados podemos calcular el coeficiente de determinación: \[ R^{2} = 1-\frac{SS_{res}}{SS_{T}}. \] A medida que agregamos mas covariables al modelo el \(R^{2}\) aumenta (o permanece igual), sin importar si la covariable agregada tiene una contribución importante en el ajuste. Esto hace que sea difícil determinar si el incremento en el \(R^{2}\) al agregar una covariable sea relevante. Por esta razón, también podemos usar el coeficiente de determinación ajustado: \[ R^{2}_{adj} = 1-\frac{SS_{res}/(n-p)}{SS_{T}/(n-1)} = 1 - \frac{MS_{res}}{SS_T/(n-1)}. \] Aunque no tiene interpretación, el \(R^{2}_{adj}\) puede usarse para comparar modelos al agregar covariables. Dado que \(SS_{T}/(n-1)\) es constante, el \(R^{2}_{adj}\) solo aumentará al agregar una covariable nueva al modelo si la adición de la covariable reduce el \(MS_{res}\).

2.3.2 Pruebas individuales sobre los coeficientes

Al rechazar \(H_{0}\) de la prueba de hipótesis (2.3) concluimos que al menos un coeficiente es diferente de cero. Por lo tanto, una o más covariables tienen un aporte significativo en el modelo. El paso que sigue es identificar estas covariables.

Para esto podemos plantear las siguientes hipótesis individuales sobre los coeficientes del modelo: \[ H_{0}: \beta_{j} = 0 \qquad H_{1}: \beta_{j} \neq 0. \] El estadística de prueba es: \[ t_{0} = \frac{\widehat{\beta}_{j}}{se(\widehat{\beta}_{j})} = \frac{\widehat{\beta}_{j}}{\sqrt{MS_{res}c_{jj}}}, \] donde \(c_{jj}\) es la entrada \((j,j)\) de la matriz \(\boldsymbol C= (\boldsymbol X'\boldsymbol X)^{-1}\). Rechazamos \(H_{0}\) si \(|t_{0}| > t_{1-\alpha/2,n-p}\).

Este es una prueba parcial, puesto que estamos evaluando la significancia de \(x_{j}\) cuando las demás covariables \(x_{k}\), para \(k\neq j\), ya están incluidas en el modelo. Por lo tanto, si no rechazamos \(H_{0}\), podemos concluir que, cuando los demás regresores están en el modelo, la covariable \(x_{j}\) no tiene un aporte significativo. Por lo tanto, podríamos retirarla del modelo.

2.3.3 Pruebas sobre subconjuntos de coeficientes

Para probar la significancia de un subconjunto de coeficientes del modelo hacemos uso de la suma de cuadrados extra. Primero, consideremos el siguiente modelo de regresión: \[ \boldsymbol y= \boldsymbol X\boldsymbol \beta+ \boldsymbol \varepsilon, \] donde \(\boldsymbol X\) es una matrix \(n \times p\) y \(\boldsymbol \beta\) es el vector de coeficientes de longitud \(p\). Queremos probar si un subconjunto \(r < p\) de covariables tienen un aporte significativo en el modelo. Para esto hacemos la siguiente partición del vector \(\boldsymbol \beta\): \[ \boldsymbol \beta= \begin{pmatrix} \beta_{0} \\ \beta_{1} \\ \vdots \\ \beta_{p-r-1} \\ \hline \beta_{p-r} \\ \beta_{p-r+1} \\ \vdots \\ \beta_{p} \end{pmatrix} = \begin{pmatrix} \boldsymbol \beta_{1} \\ \hline \boldsymbol \beta_{2}\end{pmatrix}, \] donde \(\boldsymbol \beta_{1}\) y \(\boldsymbol \beta_{2}\) son vector de dimensión \((p-r)\) y \((r)\), respectivamente. Por lo tanto, queremos realizar la siguiente prueba de hipótesis: \[\begin{equation} H_{0}: \boldsymbol \beta_{2} = \boldsymbol 0\qquad H_{1}: \boldsymbol \beta_{2} \neq \boldsymbol 0. \tag{2.5} \end{equation}\] El modelo anterior se puede re-escribir de la siguiente forma: \[ \boldsymbol y= \boldsymbol X\boldsymbol \beta+ \boldsymbol \varepsilon= \boldsymbol X_{1}\boldsymbol \beta_{1}+ \boldsymbol X_{2}\boldsymbol \beta_{2} + \boldsymbol \varepsilon, \] donde \(\boldsymbol X_{1}\) es la matriz \(n\times (p-r)\) que contiene las columnas de \(\boldsymbol X\) asociadas con \(\boldsymbol \beta_{1}\), y \(\boldsymbol X_{2}\) es la matriz \(n\times r\) que contiene las columnas de \(\boldsymbol X\) asociadas con \(\boldsymbol \beta_{2}\). Este es llamado el modelo completo.

Para el modelo completo tenemos:

• Estimador de \(\boldsymbol \beta\): \[ \widehat{\boldsymbol \beta}= (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y. \]
• Suma de cuadrados del modelo: \[ SS_{R}(\boldsymbol \beta) = \boldsymbol y'(\boldsymbol H- \frac{1}{n}\boldsymbol 1\boldsymbol 1')\boldsymbol y. \]
• Cuadrado medio del error: \[ MS_{res} = \frac{\boldsymbol y'(\boldsymbol I- \boldsymbol H)\boldsymbol y}{n-p}. \]

Para evaluar la contribución de los regresores asociados a \(\boldsymbol \beta_{2}\), ajustamos el modelo asumiendo que \(H_{0}\) es cierta. De esta forma tenemos el modelo reducido: \[ \boldsymbol y= \boldsymbol X_{1}\boldsymbol \beta_{1} + \boldsymbol \varepsilon. \] Para el modelo reducido tenemos:

• Estimador de \(\boldsymbol \beta_{1}\): \[ \widehat{\boldsymbol \beta}_{1} = (\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'\boldsymbol y. \]
• Suma de cuadrados del modelo: \[ SS_{R}(\boldsymbol \beta_{1}) = \boldsymbol y'(\boldsymbol H_1 - \frac{1}{n}\boldsymbol 1\boldsymbol 1')\boldsymbol y, \] con \(\boldsymbol H_1 = \boldsymbol X_1(\boldsymbol X_1'\boldsymbol X_1)^{-1}\boldsymbol X_1'\).

Entonces, la suma de cuadrados debido a \(\boldsymbol \beta_{2}\) dado que \(\boldsymbol \beta_{1}\) ya está en el modelo es: \[ SS_{R}(\boldsymbol \beta_{2}| \boldsymbol \beta_{1}) = SS_{R}(\boldsymbol \beta) - SS_{R}(\boldsymbol \beta_{1}), \] Esta suma de cuadrados es llamada la suma de cuadrados extra debido a \(\boldsymbol \beta_2\) puesto que mide el incremento en la suma de cuadrados de la regresión como resultado de adicionar los regresores \(\boldsymbol X_{2}\) en el modelo que ya contiene \(\boldsymbol X_{1}\).

Se puede probar que \(SS_{R}(\boldsymbol \beta_{2}| \boldsymbol \beta_{1})\) y \(MS_{res}\) son independientes. Por lo tanto, podemos utilizar el siguiente estadístico de prueba: \[ F_{0} = \frac{SS_{R}(\boldsymbol \beta_{2}|\boldsymbol \beta_{1})/r}{MS_{res}}. \] Si \(H_{0}\) es cierta entonces \(F_{0} \sim F_{r,n-p}\). Si \(H_{0}\) no es cierta, entonces \(F_{0}\) sigue una distribución \(F\) no-central con parámetro de no centralidad igual a: \[ \lambda = \frac{1}{\sigma^{2}}\boldsymbol \beta_{2}'\boldsymbol X_{2}'\left[ \boldsymbol I_{n} - \boldsymbol X_{1}(\boldsymbol X_{1}'\boldsymbol X_{1})^{-1}\boldsymbol X_{1}'\right]\boldsymbol X_{2}\boldsymbol \beta_{2}. \] Note que si hay una relación casi colineal entre \(\boldsymbol X_{1}\) y \(\boldsymbol X_{2}\) (multicolinealidad), \(\lambda\) es cercano a cero pesar que \(\boldsymbol \beta_{2}\) sea marcadamente distinto de cero. Es decir, que la prueba tiene poca capacidad de indicar diferencias (poco poder) en presencia de multicolinealidad. Caso contrario, el máximo poder se alcanza cuando \(\boldsymbol X_{1}\) y \(\boldsymbol X_{2}\) son ortogonales (es decir \(\boldsymbol X_{2}'\boldsymbol X_{1} = \boldsymbol 0\)).

Entonces, si \(F_{0} > F_{1-\alpha,r,n-p}\) rechazamos \(H_{0}\) y concluimos que al menos un coeficiente en \(\boldsymbol \beta_{2}\) es diferente de cero. Consecuentemente, al menos una de las covariables en \(\boldsymbol X_{2}\) tiene un aporte significativo dentro del modelo.

Ejemplo

Considere el modelo: \[ y_{i} = \beta_{0} + \beta_{1}x_{i1} + \beta_{2}x_{i2} + \beta_{3}x_{i3} + \varepsilon_{i}. \] La suma de cuadrados del modelo se puede descomponer de la siguiente forma: \[ SS_{R}=SS_{R}(\beta_{1},\beta_{2},\beta_{3}| \beta_{0}) = SS_{R}(\beta_{1}|\beta_{0}) + SS_{R}(\beta_{2}|\beta_{0},\beta_{1}) + SS_{R}(\beta_{3}|\beta_{0},\beta_{1},\beta_{2}), \] donde cada suma de cuadrados en el lado derecho tiene un grado de libertad. Además, el order de los regresores en estos componentes marginales es arbitrario. Por lo que la siguiente descomposición alternativa es también válida: \[ SS_{R}(\beta_{1},\beta_{2},\beta_{3}| \beta_{0})=SS_{R}(\beta_{2}|\beta_{0}) + SS_{R}(\beta_{3}|\beta_{0},\beta_{2}) + SS_{R}(\beta_{1}|\beta_{0},\beta_{2},\beta_{3}). \]

Sin embargo, la siguiente partición de la suma de cuadrados de la regrsión es generalmente inválida: \[ SS_{R}(\beta_{1},\beta_{2},\beta_{3}| \beta_{0})\neq SS_{R}(\beta_{1}|\beta_{0},\beta_{2},\beta_{3}) + SS_{R}(\beta_{2}|\beta_{0},\beta_{1},\beta_{3}) + SS_{R}(\beta_{3}|\beta_{0},\beta_{1},\beta_{2}). \]

2.4 Prueba de hipótesis lineal general

Suponga que estamos interesados en las siguientes hipótesis: \[\begin{equation} H_{0}: \boldsymbol T\boldsymbol \beta=\boldsymbol 0\qquad H_{1}: \boldsymbol T\boldsymbol \beta\neq \boldsymbol 0, \tag{2.6} \end{equation}\] donde \(\boldsymbol T\) es una matriz \(m \times p\) de constantes, tal que \(r\) de las \(m\) ecuaciones de \(\boldsymbol T\boldsymbol \beta=\boldsymbol 0\) son independientes.

El modelo completo (FM) es: \[ \boldsymbol y=\boldsymbol X\boldsymbol \beta+\boldsymbol \varepsilon, \] El estimador de \(\boldsymbol \beta\) es \(\widehat{\boldsymbol \beta}= (\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y\), y la suma de cuadrados de los residuos es \(SS_{res}(FM)\) (con \(n-p\) grados de libertad).

El modelo reducido (RM) se obtiene al resolver las \(r\) ecuaciones independientes de \(\boldsymbol T\boldsymbol \beta= \boldsymbol 0\) para los \(r\) coeficientes en el modelo completo en términos de los \(p-r\) coeficientes restantes. Esto lleva al siguiente RM: \[ \boldsymbol y=\boldsymbol Z\boldsymbol \gamma+\boldsymbol \varepsilon, \] donde \(\boldsymbol Z\) es una matriz \(n\times (p-r)\) y \(\boldsymbol \gamma\) es un vector de dimiensión \((p-r)\) de coeficientes de regresión. La suma de cuadrados de los residuos de este modelo es \(SS_{res}(RM)\) (con \(n-p+r\) grados de libertad).

Dado que el modelo reducido tiene menos parámetros que el modelo completo, \(SS_{res}(RM) \geq SS_{res}(FM)\). Para probar (2.6) usamos la diferencia entre las sumas de cuadrados de los residuos: \[ SS_{H} = SS_{res}(RM) - SS_{res}(FM), \] con \(r\) grados de libertad. \(SS_{H}\) es llamado la suma de cuadrados debido a \(H_{0}:\boldsymbol T\boldsymbol \beta=\boldsymbol c\). El estadístico de prueba es: \[ F_{0} = \frac{SS_{H}/r}{SS_{res}(FM)/(n-p)} = \frac{\widehat{\beta}'\boldsymbol T[\boldsymbol T(\boldsymbol X'\boldsymbol X)\boldsymbol T']^{-1}\boldsymbol T\widehat{\boldsymbol \beta}/r}{SS_{res}(FM)/(n-p)}. \] Rechazamos \(H_{0}\) si \(F_{0} > F_{1-\alpha,r,n-p}\).

La hipótesis anterior se puede generalizar de la siguiente forma: \[\begin{equation} H_{0}: \boldsymbol T\boldsymbol \beta=\boldsymbol c\qquad H_{1}: \boldsymbol T\boldsymbol \beta\neq \boldsymbol c, \tag{2.7} \end{equation}\] Para este caso, el estadístico de prueba es: \[ F_{0} = \frac{(\boldsymbol T\widehat{\boldsymbol \beta}-\boldsymbol c)'[\boldsymbol T(\boldsymbol X'\boldsymbol X)\boldsymbol T']^{-1}(\boldsymbol T\widehat{\boldsymbol \beta}-\boldsymbol c)/r}{SS_{res}(FM)/(n-p)}. \] Si \(H_{0}\) es cierta, \(F_{0}\sim F_{r,n-p}\). Por lo tanto, rechazamos \(H_{0}\) si \(F_{0} > F_{1-\alpha,r,n-p}\).

ejemplo

Considere el modelo: \[ y_{i} = \beta_{0} + \beta_{1}x_{i1}+ \beta_{2}x_{i2}+ \beta_{3}x_{i3}+ \beta_{3}x_{i3} + \varepsilon_{i}, \] y queremos probar las siguientes hipótesis: \[\begin{align*} H_{0}:& \beta_{1}=0 & H_{1}:&\beta_{1}\neq 0 \\ & 2\beta_{2}-\beta_{3}=3 & &2\beta_{2}-\beta_{3}\neq 3 \\ \end{align*}\] De aquí tenemos que: \[ \boldsymbol T= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 2 & -1 & 0 \\ \end{pmatrix} \mbox{ y } \boldsymbol c= \begin{pmatrix} 0 \\ 3 \end{pmatrix}. \] Si no rechazamos \(H_{0}\), podríamos estimar \(\boldsymbol \beta\) sujo a las restricciones impuestar por la hipótesis nula (usando mínimos cuadrados restringidos).

Bajo peso al nacer - pruebas de hipótesis

Los resultados de las pruebas de hipótesis individuales sobre los coeficientes, análisis de varianza y coeficientes de determianción se obtiene a partir del resumen del modelo:

summary(mod)

## 
## Call:
## lm(formula = weight ~ age + mppwt, data = birthweight)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.79566 -0.34083  0.05415  0.26504  0.88930 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -3.977501   1.053336  -3.776 0.000531 ***
## age          0.167456   0.026585   6.299 1.99e-07 ***
## mppwt        0.011416   0.009756   1.170 0.249032    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4356 on 39 degrees of freedom
## Multiple R-squared:  0.5503, Adjusted R-squared:  0.5273 
## F-statistic: 23.87 on 2 and 39 DF,  p-value: 1.703e-07

A partir de estos resutados tenemos que \(F_{0}=23.8665\) con un valor-\(p\) asociado de \(0.000\), es decir que al menos uno de los coeficientes de regresión es diferente de cero. Además, el \(55\)% de la variabilidad del peso al nacer es explicada por la edad gestacional y el peso de la madre antes del embarazo \((R^{2}=0.5503)\). Note que hubo un incremento leve en el \(R^{2}\) respecto al modelo que solo incluye la edad gestacional como covariable (\(R^{2} = 0.535\)).

A partir de las pruebas de hipótesis individuales, podemos decir que el peso de la madre antes del embarazo no tiene un aporte significativo cuando el modelo ya incluye la covariable edad gestacional (\(t_{0}=1.17\) con un valor-\(p\) asociado de 0.249). Por otro lado, el efecto de la edad gestacional si es significativo (\(t_{0}=6.3\) con un valor-\(p\) asociado de 0).

Ahora consideremos un modelo ingresando dos covariables más: \[ y_{i} = \beta_{0} + \beta_{1}\mbox{age}_{i} + \beta_{2}\mbox{mppwt}_{i} + \beta_{3}\mbox{motherage}_{i} + \beta_{2}\mbox{mnocig}_{i} + \varepsilon_{i}, \] donde \(\mbox{motherage}_{i}\) y \(\mbox{mnocig}_{i}\) es la edad (en años) y el número medio de cigarrillos fumados por mes de la \(i\)-ésima madre, respectivamente. El resumen del modelo ajustado es:

mod.completo = lm(weight~age + mppwt + motherage + mnocig,data=birthweight)
summary(mod.completo)

## 
## Call:
## lm(formula = weight ~ age + mppwt + motherage + mnocig, data = birthweight)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.78765 -0.35948  0.09209  0.35024  0.75018 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -4.104029   1.011723  -4.056 0.000247 ***
## age          0.168027   0.024916   6.744 6.24e-08 ***
## mppwt        0.014838   0.009530   1.557 0.127966    
## motherage    0.001751   0.012335   0.142 0.887900    
## mnocig      -0.014417   0.005421  -2.660 0.011493 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4073 on 37 degrees of freedom
## Multiple R-squared:  0.627,  Adjusted R-squared:  0.5867 
## F-statistic: 15.55 on 4 and 37 DF,  p-value: 1.5e-07

Respecto al modelo anterior, hay un aumento del \(R^{2}\) y el \(R^{2}_{adj}\). Por lo cuál podemos concluir que al ingresar estas covariables el ajuste mejoró. Aunque, los efectos del peso y la edad de la madre no son significativos a partir de las pruebas individuales.

Esto no necesariamente quiere decir que podemos eliminar estas dos covariables del modelo, recordemos que las pruebas \(t\) son individuales (se evalúa el efecto de la covariable cuando el modelo ya incluye las restantes). Para determinar si podemos eliminar mppwt y motherage del modelo, realizamos la siguiente prueba de hipótesis: \[ H_{0}: \beta_{2} = \beta_{3} = 0 \qquad H_{0}: \beta_{j} \neq 0 \mbox{ para algún }j=2,3. \] En R podemos hacer esto a través de la función anova:

mod.reducido = lm(weight~age + mnocig,data=birthweight)
anova(mod.reducido,mod.completo)

## Analysis of Variance Table
## 
## Model 1: weight ~ age + mnocig
## Model 2: weight ~ age + mppwt + motherage + mnocig
##   Res.Df    RSS Df Sum of Sq      F Pr(>F)
## 1     39 6.5912                           
## 2     37 6.1386  2   0.45258 1.3639 0.2682

Aquí vemos que \(F_{0}= 1.364\) con un valor-\(p\) asociado de \(0.2682\). Por lo tanto, no tenemos evidencia suficiente para rechazar \(H_{0}\) y podemos retirar las dos covariables del modelo.

2.5 Intervalos de confianza

Al igual que en caso del modelo lineal simple, también podemos hacer estimaciones por intervalos de confianza para los coeficientes del modelo, valor esperado de \(Y\) y observaciones futuras.

Para que los intervalos de confianza sean válidos se requiere que se cumplan todos los supuestos del modelo, esto es \(\boldsymbol \varepsilon\sim N(\boldsymbol 0, \sigma^{2}\boldsymbol I_{n})\).

2.5.1 Intervalos de confianza para \(\beta_{j}\)

El intervalo de confianza de \(\beta_{j}\) parte de: \[ \frac{\widehat{\beta}_{j} - \beta_{j}}{\sqrt{V(\widehat{\beta}_{j})}} = \frac{\widehat{\beta}_{j} - \beta_{j}}{\sqrt{MS_{res}c_{jj}}} \sim t_{n-p}, \] donde \(c_{jj}\) es la entrada \((j,j)\) de la matriz \(\boldsymbol C=(\boldsymbol X'\boldsymbol X)^{-1}\). Entonces, el intervalo del \((1-\alpha)100\%\) de confianza para \(\widehat{\beta}_{j}\) es: \[ \widehat{\beta}_{j} \pm t_{1-\alpha/2,n-p}\sqrt{MS_{res}c_{jj}}. \]

2.5.2 Intervalos de confianza para el valor esperado de \(Y\) y una observación futura

Ahora queremos construir un intervalo de confianza para la respuesta media de \(Y\) para un punto particular \(\boldsymbol x_{0}=(1,x_{01},x_{02},\ldots,x_{0,p-1})\). La estimación puntual en \(\boldsymbol x_{0}\) es: \[ \widehat{\mu}_{Y|\boldsymbol x_0} = \boldsymbol x_{0}'\widehat{\boldsymbol \beta}. \] Además, tenemos que \(\widehat{\mu}_{Y|\boldsymbol x_0} \sim N[\boldsymbol x_{0}'\boldsymbol \beta, V(\widehat{\mu}_{Y|\boldsymbol x_0})]\) con: \[ V(\widehat{\mu}_{Y|\boldsymbol x_0}) = \sigma^{2}\boldsymbol x_{0}'(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol x_{0}. \] Por lo tanto, el intervalo del \((1-\alpha)100\%\) de confianza para \(E(Y|\boldsymbol x_{0})\) es: \[ \widehat{\mu}_{Y|\boldsymbol x_0} \pm t_{1-\alpha/2,n-p}\sqrt{MS_{res}\boldsymbol x_{0}'(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol x_{0}}. \] De igual forma, el intervalo del \((1-\alpha)100\%\) de confianza para una observación futura en \(\boldsymbol x_{0}\) es: \[ \widehat{\mu}_{Y|\boldsymbol x_0} \pm t_{1-\alpha/2,n-p}\sqrt{MS_{res}\left[1+ \boldsymbol x_{0}'(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol x_{0}\right]}. \]

Bajo peso al nacer - intervalos de confianza

Siguiendo con el modelo inicial \(y_{i}=\beta_{0}+\beta_{1}\mbox{age}_{i}+\beta_{2}\mbox{mppwt}_{i}+\varepsilon_{i}\), los intervalos del 95% de confianza para los coeficientes son:

confint(mod)

##                    2.5 %     97.5 %
## (Intercept) -6.108074493 -1.8469278
## age          0.113682140  0.2212300
## mppwt       -0.008317269  0.0311501

Si peso de la madre permance constante, por cada aumento de una semana en la edad gestacional, el peso medio del recién nacido incrementa entre \(114\) y \(221\) gramos con un nivel de confianza del 95%. Note que el intervalo de confianza para el coeficiente asociado al peso de la madre contiene el valor \(0\) (recordemos que no rechazamos la hipótesis nula de la prueba \(t\) sobre \(\beta_{2}\)).

Queremos determinar el peso medio de los recién nacidos en la semana gestacional \(36\) y de madres que pesan 50 kilogramos. Es decir \(E(Y|\mbox{age}=36, \mbox{mppwt}=50)\). Para esto podemos contruir un intervalo del 95% de confianza:

x0 = data.frame(age=36,mppwt=50)
predict(mod,x0,interval='confidence')

##        fit      lwr      upr
## 1 2.621739 2.386238 2.857239

Por lo tanto, el peso medio de los recién nacidos en la semana gestacional 36 y de madres que pesan 50 kilogramos está entre \(2.39\) y \(2.86\) kilogramos con un nivel de confianza del 95%.

Ahora, estamos interesados en predecir el peso de un recién nacido en la semana \(38\) y cuya madre peso \(65\) kilogramos. Por lo cuál construimos un intervalo del 95% de predicción:

x0pred = data.frame(age=38,mppwt=65)
predict(mod,x0pred,interval='prediction')

##        fit     lwr      upr
## 1 3.127897 2.21775 4.038044

El peso del recién nacido con estas caracteristica está entre \(2.22\) y \(4.04\) kilogramos con un nivel de confianza del 95%.

2.6 Extrapolación oculta en regresión múltiple

Al igual que en regresión simple, al pronosticar una nueva respuesta en un punto dado \(\boldsymbol x_{0}\) se debe tener cuidado de no extrapolar fuera de la región de los datos originales. En regresión múltiple es fácil extrapolar inadvertidamente, puesto que la región que contiene los datos está definida de forma conjunta por los valores que toman las covariables y no por el rango individual de cada covariable.

La Figura 2.2 muestra un ejemplo de extrapolación en el caso de un modelo de regresión con dos covariables. Se quiere hacer una predicción en el punto \((x_{01},x_{02})\) que está dentro del rango de ambos regresores, pero que fuera de la región conjunta de los datos (región roja en la figura). Por lo tanto, al realizar la predicción en este punto estaríamos extrapolando.

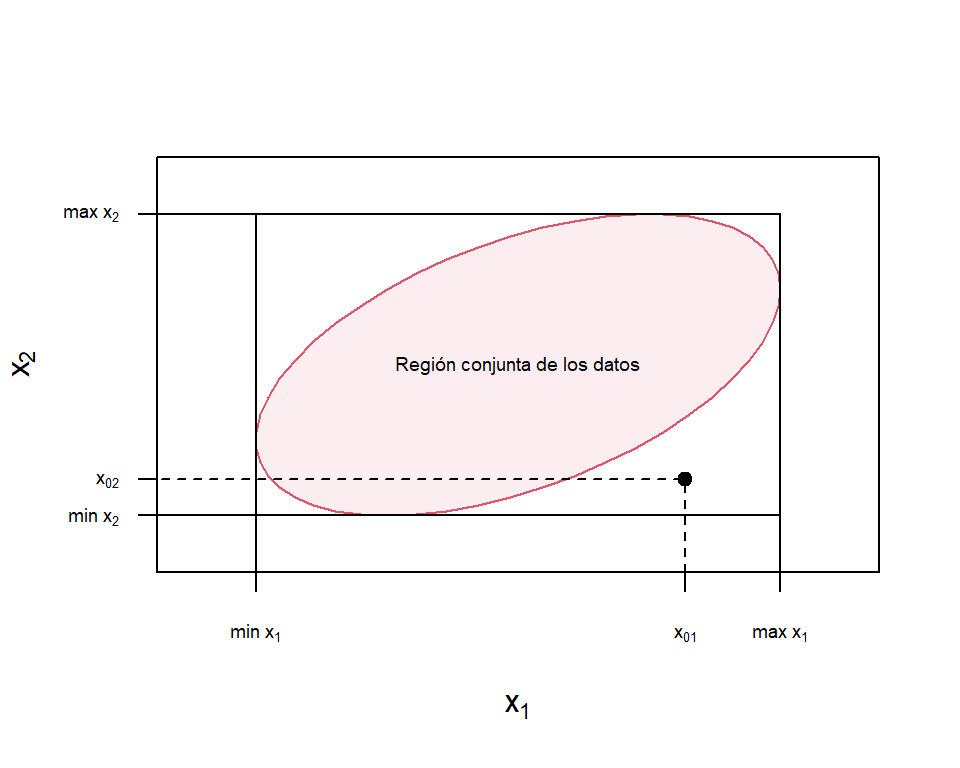
Figure 2.2: Ejemplo de extrapolación en regresión múltiple

Determinar la región conjunta de los datos en regresión múltiple no es fácil, lo que hace díficil saber si se está extrapolando a la hora de hacer de una predicción. Por lo tanto, se ha propuesto determinar la región conjunta de los datos a partir del conjunto convexo mínimo que contiene todos los \(n\) datos originales, \((x_{i1}; x_{i2},\ldots,x_{i,p-1})\), para \(i = 1,2,\ldots,n\), como la envolvente de las covariables (RVH). Entonces, si un punto \((x_{01},x_{02}, \ldots,\ldots, x_{0,p-1})\) está dentro o en la frontera de la RVH, una prediccón o una estimación implica interpolación, mientras que si está fuera de la RVH, se está extrapolando.

Una aproximación de la RVH es a través de la matriz \(\boldsymbol H\). El conjunto de puntos \(\boldsymbol x\) que satisfacen, \(\boldsymbol x'(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol x\leq \max(h_{ii})\), prudcen un elipsoide que encierra todos los puntos dentro de la \(RVH\). Entonces, un punto de predicción \(\boldsymbol x_{0}\) está fuera de la RVH si \(h_{00} > \max{h_{ii}}\), donde: \[ h_{00} = \boldsymbol x'_{0}(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol x_{0}. \]

Bajo peso al nacer - interpolación

Suponga que se quiere hacer una predicción para recién nacidos con las características que muestra la Tabla 2.1.

Table 2.1: Bajo peso al nacer. Punto de predicción.

	1	2	3	4
Edad gestacional (semanas)	34	36	38	46
Peso de la madre (kg)	75	50	60	55

La Figura 2.3 muestra el gráfico de dispersión de las covariables, donde los puntos rojos indican los valores donde se quieren hacer predicciones. Aquí vemos que en los puntos \(\boldsymbol x_{02}\) y \(\boldsymbol x_{03}\) no estaríamos extrapolando. Pero, es difícil de determinar para los puntos \(\boldsymbol x_{01}\) y \(\boldsymbol x_{04}\). Para esto vamos a calcular las aproximaciones de la RVH y verificar si en estos puntos estaríamos extrapolando.

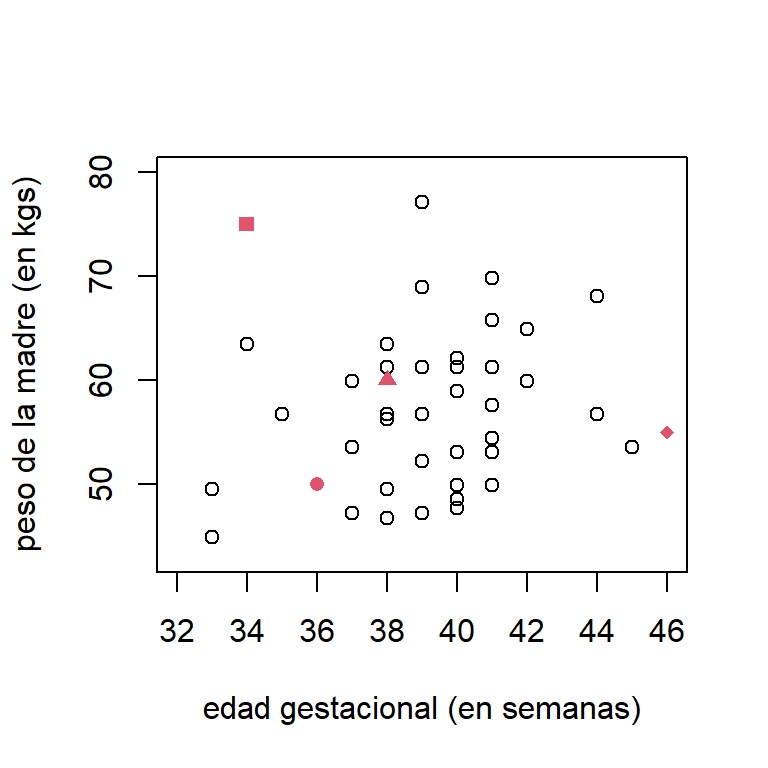
Figure 2.3: Bajo peso al nacer. Gráfico de dispersion de la edad gestacional y el peso de la madre antes del embarazo. Los puntos donde se quiere hacer predicción están en rojo.

newPoints = cbind(x0=rep(1,4),x1=c(34,36,38,46),x2=c(75,50,60,55))
X = model.matrix(mod)
XtX.inv = solve(t(X)%*%X)
h.values = hatvalues(mod)
hmax = max(h.values)
h0 = apply(newPoints,1,function(x){t(x)%*%XtX.inv%*%x})
h0 >hmax

## [1]  TRUE FALSE FALSE FALSE

Para la predicción en el punto \(\boldsymbol x_{01}\), tenemos que \(h_{0} = (1, 34, 77)(\boldsymbol X'\boldsymbol X)^{-1}(1, 34, 77)' = 0.3487\) \(>\) \(h_{max} = 0.2276\). Por lo tanto, aquí se estaría extrapolando. Para el resto de punto no hay problemas de extrapolación.

2.6.1 Coeficientes normalizados de regresión

Los coeficientes de regresión están influenciados por las unidades de medida de las covariables. Exactamente las unidades de medida de \(\beta_{j}\) es: \[ \frac{\mbox{la unidad de medida de }y }{\mbox{la unidad de medida de }x_{j}}. \] Dado que, por lo general, las covariables están medidas en unidades diferenes, la comparación de los coeficientes es complicada. En el ejemplo de los datos de los recién nacidos, la edad gestacional está en semanas y el peso de la madre en kilogramos.

Por esta razón, en algunas ocasiones es útil escalar los valores de las covariables y la respuesta para calcular los coeficientes de regresión adimensionales. Hay varias formas de hacer este escalamiento, aquí nos centraremos en el escalamiento de longitud unitaria.

2.6.1.1 Escalamiento de longitud unitaria

Una opción es hacer un escalamiento de longitud unitaria a las covariables: \[ z_{ij} = \frac{x_{ij}-\bar{x}}{\sqrt{S_{jj}}}, i=1,2,\ldots,n \quad j=1,2,\ldots,p-1, \] y la variable respuesta: \[ y_{i}^{*} = \frac{y_{i}-\bar{y}}{\sqrt{SS_{T}}}, \] donde: \[ S_{jj} = \sum_{i=1}^{n}(x_{ij} - \bar{x}_{j})^{2}. \] Con estas variables transformadas, se puede ajustar el modelo: \[ y_{i}^{*} = b_{1}z_{i1} + b_{2}z_{i2} + \ldots + b_{p-1}z_{i,p-1} = \boldsymbol z_{i}'\boldsymbol b+ \boldsymbol \varepsilon. \] El estimador por MCO es: \[ \widehat{\boldsymbol b}= (\boldsymbol Z'\boldsymbol Z)^{-1}\boldsymbol Z'\boldsymbol y^{*}. \] Note que con este escalamiento, la matriz \((\boldsymbol Z'\boldsymbol Z)\) es igual a la matriz de correlación de las covariables. Esto es: \[ (\boldsymbol Z'\boldsymbol Z) = \boldsymbol R= \begin{pmatrix} 1 & r_{12} & r_{13} & \ldots & r_{1,p-1} \\ r_{12} & 1 & r_{23} & \ldots & r_{2,p-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ r_{1,p-1} & 1 & r_{2,p-1} & \ldots & 1 \\ \end{pmatrix}, \] donde \(r_{jk}\) es la correlación entre las covariables \(x_{j}\) y \(x_{k}\). Además, la matriz \(\boldsymbol Z'\boldsymbol y^{*}\) es el vector de correlación entre la variable respuesta y cada covariable. Esto es: \[ \boldsymbol Z'\boldsymbol y^{*} = (r_{1y},r_{2y},r_{3y},\ldots,r_{p-1,y})', \] donde \(r_{jy}\) es la correlación entre la variable respuesta y la covariable \(x_j\).

Bajo peso al nacer - coeficientes de regresión con variables escaladas

Para estimar los coeficientes de regresión escalados, primero debemos escalar las variables:

y = birthweight$weight
Z = apply(X[,-1],2,function(x){(x-mean(x))/sqrt(sum((x-mean(x))^2))})
ys = (y-mean(y))/sqrt(sum((y-mean(y))^2))

Ahora procedemos a estimar el modelo con las variables escaladas:

mod.std = lm(ys~Z-1)
summary(mod.std)

## 
## Call:
## lm(formula = ys ~ Z - 1)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.19612 -0.08401  0.01335  0.06533  0.21920 
## 
## Coefficients:
##        Estimate Std. Error t value Pr(>|t|)    
## Zage     0.6986     0.1095   6.379 1.39e-07 ***
## Zmppwt   0.1298     0.1095   1.185    0.243    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.106 on 40 degrees of freedom
## Multiple R-squared:  0.5503, Adjusted R-squared:  0.5279 
## F-statistic: 24.48 on 2 and 40 DF,  p-value: 1.142e-07

Las estimaciones de los coeficientes son ahora adimensionales y podemos comparar sus magnitudes. Por lo tanto, parece que la covariable edad gestacional es más importante para determinar el peso al nacer que la covariable peso de la madre. Note que, al escalar las variables, los resultados de las pruebas de hipótesis, estimación de \(\sigma^{2}\), y los coeficientes de determinación no se ven alterados.

2.7 Multicolinealidad

Un problema que puede afectar enormente el ajuste de un modelo de regresión es la multicolinealidad. Este se presenta cuando hay una dependencia casi lineal entre las covariables.

Recordemos que el estimador por MCO es \(\widehat{\boldsymbol \beta}=(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y\). Por lo tanto es necesario que la matriz \(\boldsymbol X'\boldsymbol X\) sea no singular. En caso contrario, no es posible encontrar la inversa y las ecuaciones normales no tendrán una única solución. Cuando sucede esto se debe a que hay al menos una columna de \(\boldsymbol X\) linealmente dependiente.

En regresión se utiliza las palabras multicolinealidad cuando hay una dependencia aproximada en las columnas de \(\boldsymbol X\). Es decir que al menos una covariable puede representarse, de forma aproximada, como una relación lineal de las otras: \[ x_{ij} \approx c_{0} + c_{1}x_{i1} + \ldots + c_{j-1}x_{i,j-1} + c_{j+1}x_{i,j+1} + \ldots + + c_{p-1}x_{i,p-1}, \] para \(i=1,\ldots,n\).

Hay que aclarar que la falta de ortogonalidad no es necesariamente un inconveniente, el problema es cuando la relación lineal entre los regresores es casi perfecta, lo que provoca problemas en las inferencias que se hagan. Uno de estos problemas se ilustra a continuación con un ejemplo.

ejemplo

Considere el siguiente modelo de regresión: \[ y_{i} = \beta_{0} + \beta_{1}x_{i1} + \beta_{2}x_{i2} + \varepsilon_{i}, \mbox{ con }\varepsilon_{i}\sim N(0,\sigma^{2}), \] y se plantean dos posibles matrices de diseño: \[ \boldsymbol X_{1} = \begin{pmatrix} 1& 1 \\ 1 & 5 \\ 2 & 1 \\ 2 & 5 \\ \end{pmatrix} \mbox{ y } \boldsymbol X_{2} = \begin{pmatrix} 1& 1 \\ 1 & 2 \\ 2 & 4 \\ 2 & 5 \\ \end{pmatrix}. \] Haciendo el escalamiento de longitud unitaria a las covariables tenemos que: \[ \boldsymbol Z_{1}'\boldsymbol Z_{1} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \mbox{ y } \boldsymbol Z_{1}'\boldsymbol Z_{1} = \begin{pmatrix} 1 & 0.95 \\ 0.95 & 1 \end{pmatrix}. \] Por lo tanto, la varianza de \(\widehat{\boldsymbol b}\) para ambos casos es: \[ V(\widehat{\boldsymbol b}_{1}) = \sigma^{2}(\boldsymbol Z_{1}'\boldsymbol Z_{1})^{-1} = \sigma^{2} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}^{-1} = \sigma^{2} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}. \] y \[ V(\widehat{\boldsymbol b}_{2}) = \sigma^{2}_{0}(\boldsymbol Z_{2}'\boldsymbol Z_{2})^{-1} = \sigma^{2} \begin{pmatrix} 1 & 0.95 \\ 0.95 & 1 \end{pmatrix}^{-1} = \sigma^{2} \begin{pmatrix} 10 & 9.49 \\ 9.49 & 10 \end{pmatrix}. \] Aquí podemos ver que la varianza de \(\widehat{\boldsymbol b}_{2}\) está inflada debido a la alta correlación entre las columnas de \(\boldsymbol X_{2}\). Es 10 veces mayor que la varianza de \(\widehat{\boldsymbol b}_{1}\) (las columnas de \(\boldsymbol X_{1}\) son independientes).

En el ejemplo anterior vemos que los valores de la diagonal de la matriz \((\boldsymbol Z'\boldsymbol Z)^{-1}\) nos indican en cuanto aumenta la varianza de las estimaciones de los coeficientes debido a la multicolinealidad. Por esta razón, estos valores toman el nombre de factores de inflación de varianza (VIFs) y son uno de los indicadores para el diagnostico de este problema.

Se puede demostrar que el VIF de \(\beta_{j}\) se puede calcular como: \[ \mbox{VIF}_{j} = \frac{1}{1-R^{2}_{j}}, \] donde \(R^{2}_{j}\) es el coeficiente de determinación obtenido ajustado una regresión de \(x_{j}\) sobre las demás covariables. Si \(x_{j}\) es casi linealmente dependiente de algunos de los otros regresores, entonces \(R^{2}_{j}\) será cercano a uno y el \(VIF_{j}\) será muy alto. Generalmente, un VIF mayor de 10 indica problemas graves de multicolinealidad.

En un capítulo posterior ahondaremos más en este problema.

2.7.1 Bajo peso al nacer - factores de inflación de varianza

En el caso del peso de los recién nacidos, tenemos que los VIFs son:

library(car)
vif(mod)

##     age   mppwt 
## 1.06696 1.06696

Lo que nos indica que la varianza de las estimaciones de los coeficientes no se inflan debido a multicolinealidad. Recordemos que la correlación entre las dos covariables no es alta (0.2505155).

References

Montgomery, Douglas C., Elizabeth A. Peck, and G. Geoffrey Vining. 2012. Introduction to Linear Regression Analysis. 5th ed. Wiley.