Capítulo 5 Evaluación de puntos influyentes y atípicos
5.1 Datos de la ONU
Retomemos los datos de la ONU (UN11 de la librería alr4). El modelo propuesto es:
\[\begin{equation}
\log \mbox{fertility}_{i} = \beta_{0} + \log \mbox{ppgdp}_{i}\beta_{1} + \mbox{pctUrban}_{i}\beta_{2} + \varepsilon_{i},
\tag{5.1}
\end{equation}\]
donde \(\varepsilon_{i}\sim N(0,\sigma^{2})\) y \(cov(\varepsilon_{j},\varepsilon_{k})=0\).
El análisis de los residuos (ver Figura 5.1) muestra que el modelo está bien especificado y no hay problemas de heterocedasticidad. Sin embargo, podemos observar que algunos residuos presentan valores muy altos. La estimación de la \(\log \mbox{fertility}\) para Guinea Ecuatorial es considerablemente baja en comparación con el valor observado. Caso contrario pasa con Corea del Norte, Bosnia y Herzegovina, y Moldavia.
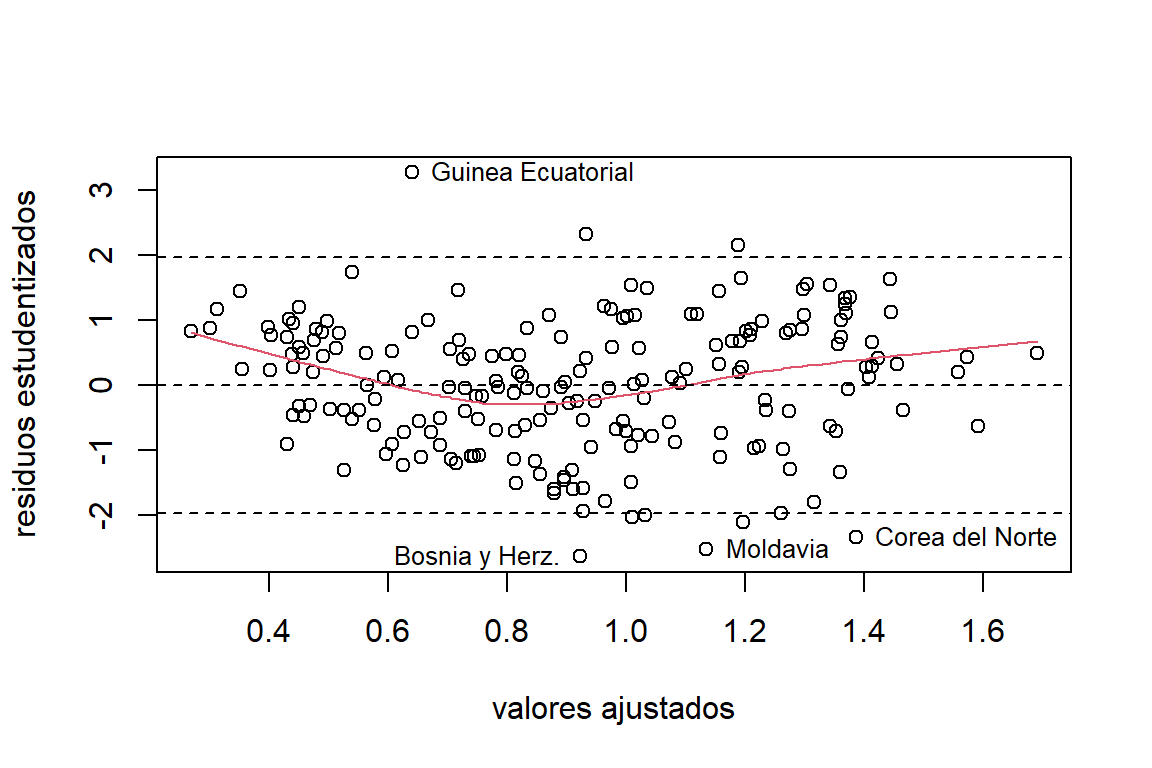
Figure 5.1: Datos de la ONU. Gráfico de los residuos estudentizados.
5.2 Importancia de detectar valores influyentes y atípicos
En el análisis de datos pueden observarse algunos valores atípicos. Como atípicas nos referimos a las observaciones que no siguen el patrón de la mayoría de los datos. En un análisis de regresión, pueden presentarse valores atípicos sobre la variable respuesta y/o sobre algunas covariables. Por lo tanto, se podría identificar diferentes tipos de puntos ``atípicos’’. Estos se pueden identificar en la Figura 5.2 para el caso de una regresión simple:
- \(A\) es un punto atípico: valor que no se ajusta bien en \(Y\), pero regular en \(X\).
- \(B\) es un punto de balanceo: observación que se ajusta bien en \(Y\), pero es inusual en \(X\).
- \(C\) es un punto de influyente: medición que no se ajusta bien en \(Y\) y es inusual en \(X\).
Estos puntos inusuales pueden ser problemáticos a la hora de ajustar un modelo lineal por MCO, ya que pueden tener mucha influencia en los resultados, y su presencia puede ser una señal de que el modelo no captura caraterísticas importantes de los datos.

Figure 5.2: Diferentes tipos de datos. A: Punto atípico, B: punto de balanceo, C: punto influyente.
En la Figura 5.3(a) vemos que un punto atípico no tiene un efecto grande en la estimación de la recta de regresión. Sin embargo, dado que los puntos atípicos generan valores altos (en valor absoluto) para los residuos, estas observaciones inflan la varianza de las estimaciones y afectan las inferencias. En este caso, la estimación de la varianza con todos los datos es de \(\widehat{\sigma}^{2}=6.37\), y si se omite el dato \(A\), tenemos que \(\widehat{\sigma}^{2}=1.55\). Como vemos en la Figura @ref{fig:puntosAIw}(b) los puntos de balanceo tampoco tienen mucha influencia sobre las estimaciones por MCO ya que estos están en línea con el resto de los datos.
Por el otro lado, en la Figura 5.3(c) vemos que los puntos influyentes afectan notablemente las estimaciones por MCO. Además, también inflan considerablemente la variabilidad. Con todos los datos tenemos que \(\widehat{\sigma}^{2}=3.09\). Mientras que \(\widehat{\sigma}^{2}=1.55\) al eliminar la observación C.
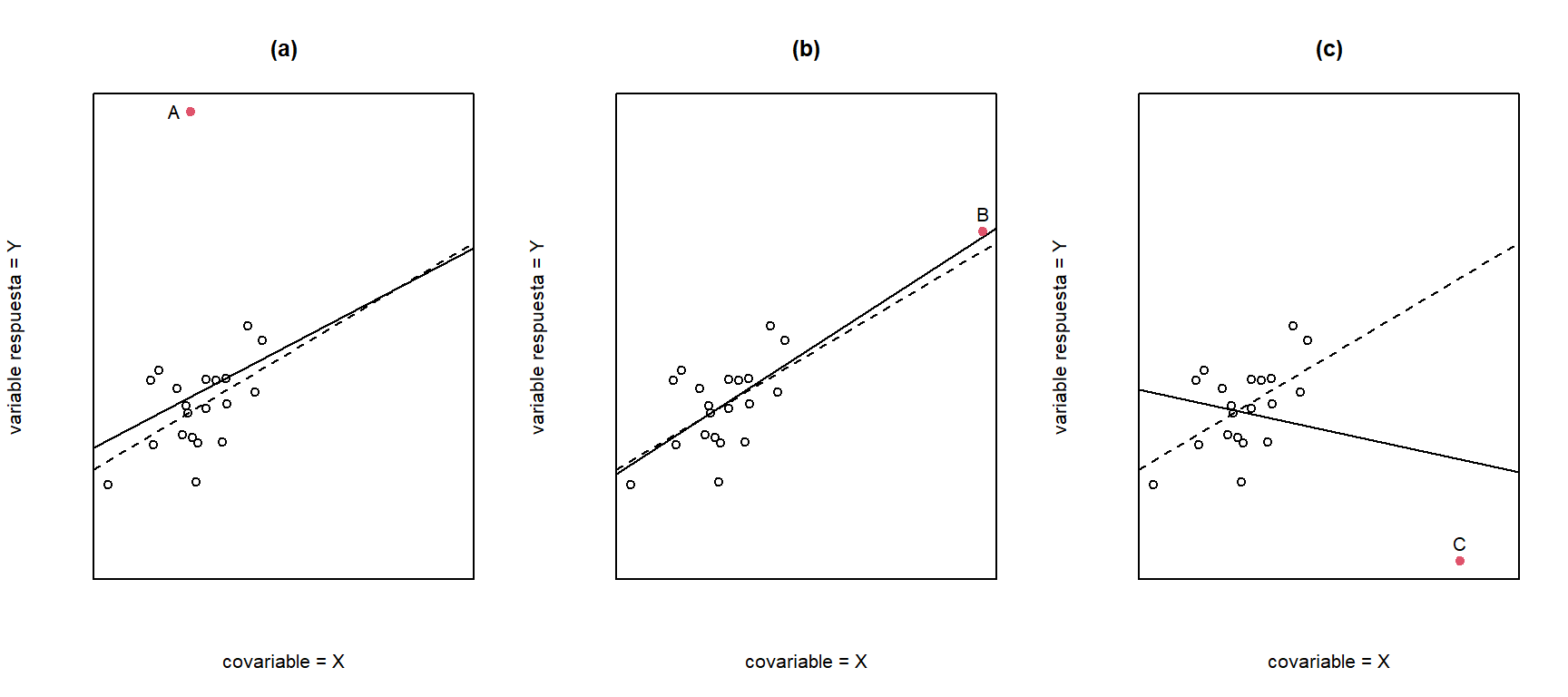
Figure 5.3: Efecto de los puntos inusuales. En cada gráfico, la línea continua es la estimación por MCO con todos los datos, mientras que la línea discontinua es la estimación por MCO omitiendo el punto inusual (circulo rojo). Izquierda: efecto de un punto atípico. Centro: efecto de un punto de balanceo. Derecha: efecto de un punto influyente.
5.3 Valores atípicos
Para identificar valores atípicos podemos hacer uso de los residuos del ajuste. Recordemos que, aunque los errores tenga varianza constante y sean incorrelacionados, los residuos no cumplen con estas propiedades. Por lo tanto, es recomendado usar los residuos estudentizados (o los residuos R-Student): \[ r_{i} = \frac{e_{i}}{\sqrt{\widehat{\sigma}^{2}(1-h_{ii})}}, i=1,\ldots,n, \] o los residuos R-Student: \[ t_{i} = \frac{e_{i}}{\sqrt{\widehat{\sigma}^{2}_{(i)}(1-h_{ii})}} = r_{i} \sqrt{\frac{n-p-1}{n-p-r_{i}^{2}}}, \] donde \(\widehat{\sigma}^{2}_{(i)}\) es la estimación de \(\sigma\) usando todas las observaciones excepto la \(i\)-ésima.
Si se cumplen los supuestos del modelo, se puede demostrar que \(r_{i}\sim t_{n-p-1}\). Los residuos estudentizados siguen también está distribución pero de forma aproximada. Por lo tanto, se pueden identificar posibles valores atípicos haciendo un gráfico de los R-Student (o residuos estudentizados) contra los valores ajustados y trazar líneas de referencia en los percentiles \(0.025\) y \(0.975\) de la distribución \(t\) con \(n-p-1\) grados de libertad.
Esta verificación no es estrictamente una prueba de hipótesis. Puesto que estamos haciendo múltiplescomparaciones de los residuos R-Student con los valores criticos de la distribución \(t\). Por lo que es necesario hacer una corrección utilizando el método de Bonferroni.
Datos de la ONU - valores atípicos
En la Figura 4.2 podemos observar que hay varios residuos que sobrepasan los puntos de corte. Particularmente, la observación de Guinea Ecuatorial presenta un residuo muy alto.5.4 Puntos de balanceo
Recordemos que la estimación de la recta de regresión es un promedio ponderado de las observaciones: \[ \widehat{\boldsymbol y}= \boldsymbol X\widehat{\boldsymbol \beta}= \boldsymbol X(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y= \boldsymbol H\boldsymbol y. \] Para la observación \(y_{i}\) tenemos que \(\widehat{y}_{i} = h_{ii}y_{i} + \sum_{k\neq i}h_{ik}y_{j}\). Particularmente, el elemento \(h_{ij}\) pueden ser visto como la cantidad de balanceo o palanqueo ejercido por la j-ésima observación \((y_i)\) sobre el \(i\)-ésimo valor ajustado (\(\widehat{y}_{i}\)).
Entonces, para detectar valores influyentes vamos a centrarnos en la matriz \((\boldsymbol H)\). El elemento \(h_{ij}\) de esta matriz se calcula como: \[\begin{equation} h_{ij} = \boldsymbol x_{i}'(\boldsymbol X'\boldsymbol X)\boldsymbol x_{j}. \tag{5.2} \end{equation}\] Algunas propiedades de la matriz \(\boldsymbol H\) son:Además, la diagonal de la matriz \(\boldsymbol H\) es una medida estandarizada de la distancia de las observaciones al centro (centroide) del espacio de \(\boldsymbol x\). Por lo tanto, valores altos en la diagonal de \(\boldsymbol H\) pueden indicarnos observaciones que son potencialmente influyentes porque están alejadas en el espacio de las covariables. Viendo (5.2), si \(h_{ii}\) es muy cercano a uno, \(\widehat{y}_{i}\) estará muy cerca de \(y_{i}\) (dado que el peso de las demás observaciones será casi cero).
Dado que \(\bar{h} = p/n\), observaciones con \(h_{ii}\) superiores a \(2p/n\) son considerados puntos de balanceo (y posibles puntos influyentes). Note que, si \(2p/n > 1\), el punto de corte no aplica.
Datos de la ONU - diagonal de la matrix hat
La Figura 5.4(a) muestra los valores de la diagonal de la matrix \(\boldsymbol H\). Aquí podemos observar que algunos países presentan valores más altos del punto de corte (\(2\frac{p}{n} = 0.0302\)). Comparado con los demás valores, el valor asociado a Trinidad y Tobago es muy alto. Por lo cuál este país lo podemos considerar como un punto de balanceo.
library(alr4)
data(UN11)
Names = rownames(UN11)
mod.UN11 = lm(log(fertility)~log(ppgdp)+pctUrban,data=UN11)
hii = hatvalues(mod.UN11)
par(mfrow=c(1,2))
plot(hii,type='h',xlab='índice',ylab='valores de la diagonal de la matrix hat')
abline(h=2*3/199,lty=2)
hii[hii>2*3/199]## Djibouti Liberia Nauru North Korea Somalia
## 0.03105290 0.03747901 0.03708513 0.03105839 0.04390710
## Sri Lanka Trinidad and Tobago
## 0.03334886 0.07590435plot(log(UN11$ppgdp),UN11$pctUrban,xlab='log del PNB per cápita',
ylab='% de población urbanas')
points(log(UN11$ppgdp)[Names=='Trinidad and Tobago'],
UN11$pctUrban[Names=='Trinidad and Tobago'],col=2,pch=19)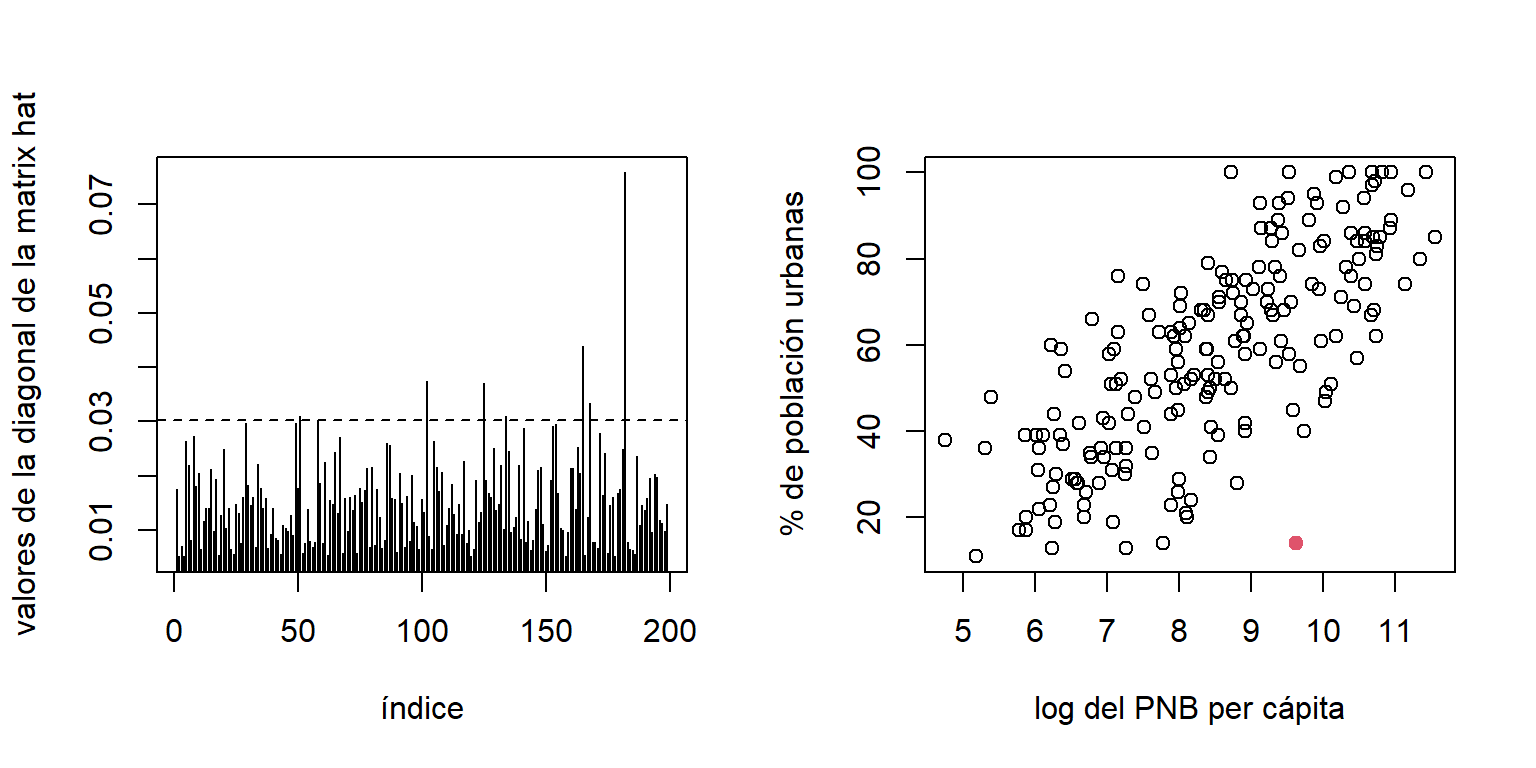
Figure 5.4: Datos de la ONU. (a) Valores de la diagonal de lam matriz hat. (b) Diagrama de dispersión de las covariables (derecha). El punto rojo indica a Trinidad y Tobago.
En laFigura 5.4(b) podemos observar que Trinidad y Tobago tiene un porcentaje muy pequeño de población en áreas urbanas y valor del PNB per cápita relativamente alto. Por esta razón el valor \(h_{ii}\) asociado es alto.
La Figura 5.5 muestra los valores de la diagonal de \(\boldsymbol H\) contra los residuos estudentizados. Aquí vemos que aunque Trinidad y Tobago tiene un valor \(h_{ii}\) alto, el R-Student asociado es bajo. Por lo que no se puede considerar como un punto influyente. Por el contrario, Guinea Ecuatorial y Corea del Norte presentan ambos valores altos (residuos y \(h_{ii}\)), por lo que se pueden considerar como puntos influyentes. Las observaciones que tienen residuos altos pero valores \(h_{ii}\) bajos se consideran como atípicos.
rstud.UN11 = res.UN11*sqrt( (199-3-1)/(199-3-res.UN11^2) )
plot(hii,rstud.UN11,ylab='r Student',
xlab='valores de la diagonal de la matrix hat')
abline(h=0,lty=2)
abline(h= c(-1,1)*qt(0.975,199-3-1),lty=2)
abline(v=2*3/199,lty=2)
text(hii[Names=="Trinidad and Tobago"],
rstud.UN11[Names=='Trinidad and Tobago'],'Trinidad y Tobago',pos=2,cex=0.8)
text(hii[Names=="Equatorial Guinea"],
rstud.UN11[Names=='Equatorial Guinea'],'Guinea Ecuatorial',pos=4,cex=0.8)
text(hii[Names=="North Korea"],
rstud.UN11[Names=='North Korea'],'Corea del Norte',pos=4,cex=0.8)
text(hii[Names=="Somalia"],
rstud.UN11[Names=='Somalia'],'Somalia',pos=4,cex=0.8)
text(hii[Names=="Bosnia and Herzegovina"],
rstud.UN11[Names=='Bosnia and Herzegovina'],'Bosnia y Herz.',pos=4,cex=0.8)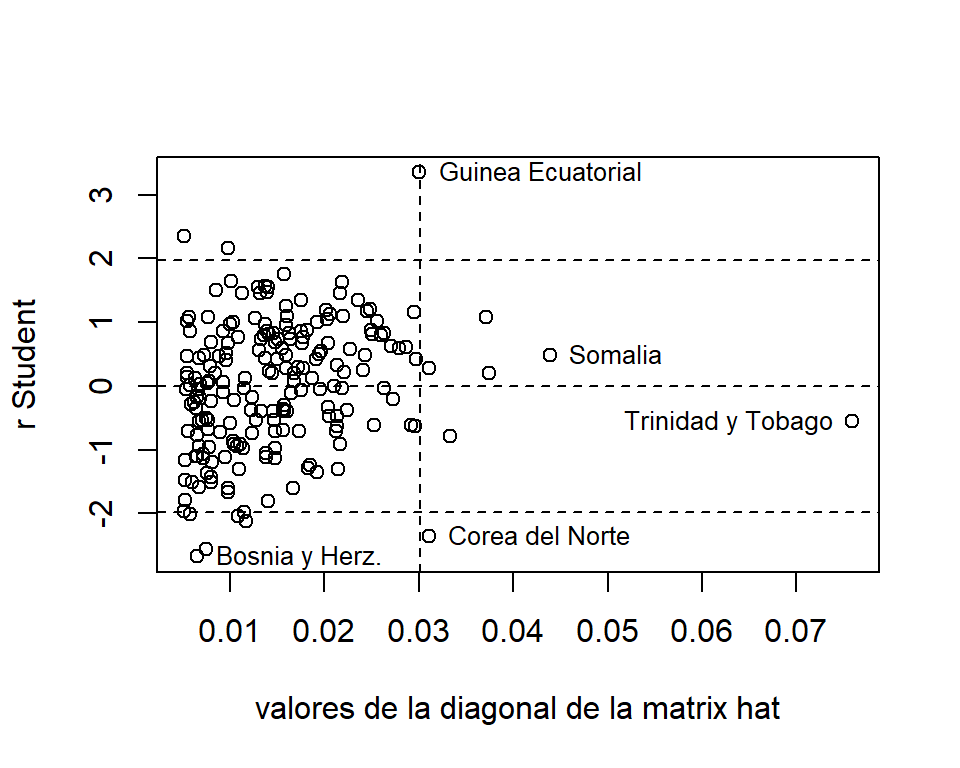
Figure 5.5: Datos de la ONU. Gráfico de valores influyentes
5.4.1 Medidas de influencia
El procedimiento para determinar si un punto es influyente se puede hacer evaluando los cambios que ocurren en el modelo ajustado cuando se elimina dicha observación.
Por ejemplo, la Figura 5.6 muestra cuanto cambian las estimaciones de \(\beta_{1}\) y \(\beta_{2}\) al eliminar un país a la vez. Aquí vemos que los cambios mas grandes ocurren cuando se eliminan a Guinea Ecuatorial o a Corea del Norte. Mientras que los países que identificamos como puntos de balanceo (Trinidad y Tobago y Somalia) o atípicos (Bosnia y Herzegovina) no tienen mucha influencia sobre las estimaciones. ….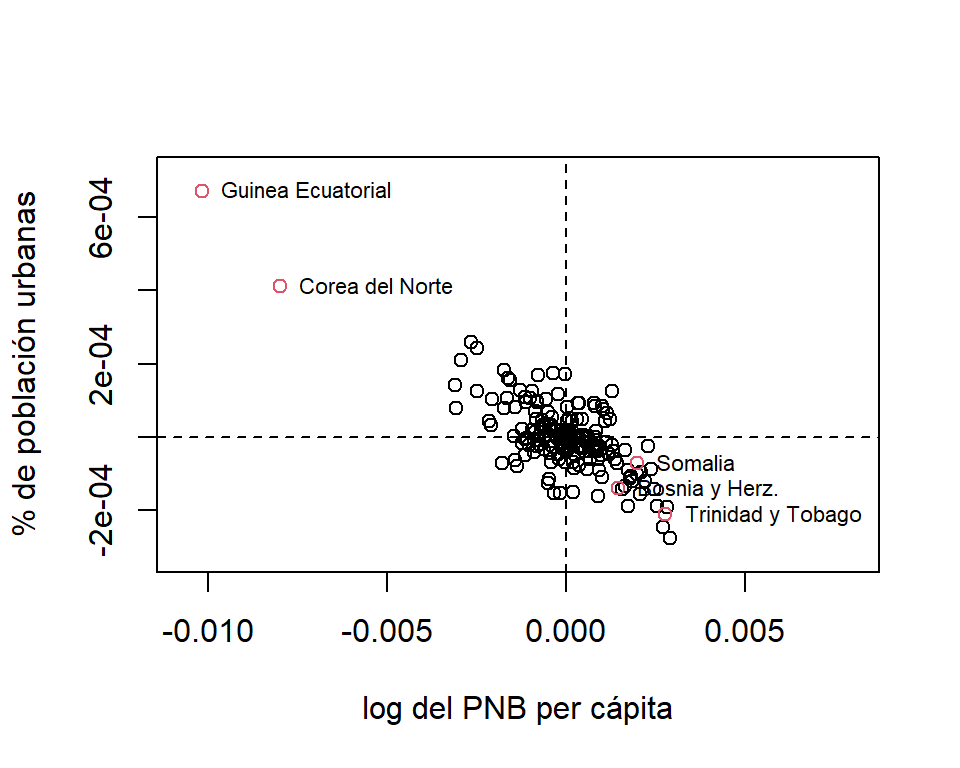
Figure 5.6: Datos de la ONU. Diferencias entre las estimaciones con todos los datos y las estimaciones obtenidas al eliminar una observación a la vez
De igual forma se podría evaluar cuanto cambian las estimaciones de \(E(y|\boldsymbol x_{i})\) o las varianzas de los coeficientes \(V(\beta_{j})\) al eliminar observaciones una a una.
A continuación se presentan algunos indicadores estadísticos para detectar puntos influyentes:
5.4.1.1 Distancia de Cook
Esta es una medida de la distancia entre las estimaciones por MCO basado en los \(n\) puntos (\(\hat{\boldsymbol \beta}\)), y el estimado obtenido eliminando el \(i\)-ésimo punto (\(\hat{\boldsymbol \beta}_{(i)}\)). Es decir que es un indicador global de cuanto cambian todas las estimaciones de los coeficientes de regresión en conjunto. Esta medida se expresa de la siguiente forma:
\[\begin{equation} \begin{split} D_{i} &= \frac{(\hat{\boldsymbol \beta}_{(i)}-\hat{\boldsymbol \beta})'\boldsymbol X'\boldsymbol X(\hat{\boldsymbol \beta}_{(i)}-\hat{\boldsymbol \beta})'}{p \hat{\sigma}^{2}} \\ &= \frac{(\hat{\boldsymbol y}_{(i)} - \hat{\boldsymbol y} )'(\hat{\boldsymbol y}_{(i)} - \hat{\boldsymbol y} )}{p\hat{\sigma}^{2}} = \frac{r_{i}^{2}}{p}\frac{h_{ii}}{1-h_{ii}}, \qquad i=1,2,\ldots,n. \end{split} \nonumber \end{equation}\]
Aquí podemos observar que \(D_{i}\) consta de dos componentes, uno asociado a el residuo \((r_{i})\) y otro a la distancia del vector \(\boldsymbol x_{i}\) al centroide de la matriz de las covariables. Ambos (o alguno de ellos) puede contribuir a valores altos de este indicador.
Entonces, los puntos asociados a valores altos de \(D_{i}\) tienen gran influencia sobre la estimación de \(\boldsymbol \beta\) por MCO. Se considera como un punto influyente si tiene asociado un \(D_{i} > 4/n\) (algunos textos sugieren \(D_{i} > 1\)).
5.4.1.2 DFBETAS
Esta medida indica cuánto cambia el coeficiente de regresión \(\hat{\beta}_{j}\), en unidades de desviaciones estándar, si se omitiera la \(i\)-ésima observación. Se calcula como: \[ DFBETAS_{(i,j)} = \frac{\hat{\beta}_{j} - \hat{\beta}_{j(i)}}{\hat{\sigma}^{2}_{(i)}C_{jj}} = \frac{r_{(j,i)}}{\sqrt{\boldsymbol r_{j}'\boldsymbol r_{j}}}\frac{t_{i}}{\sqrt{1-h_{ii}}}, \]
donde \(C_{jj}\) es el \(j\)-ésimo valor de la diagonal de \((\boldsymbol X'\boldsymbol X)^{2}\). \(\boldsymbol r_{j}\) es la \(j\)-ésima fila de \(\boldsymbol R=(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X\).
Un valor grande de \(DFBETAS_{(j,i)}\) indica que la observación \(i\) tiene gran influencia sobre el \(j\)-ésimo coeficiente de regresión. Se sugiere que si \(|DFBETAS_{(j,i)}| > 2/\sqrt{n}\) es necesario examinar la \(i\)-ésima observación.
5.4.1.3 DFFITS
Una medida que indica la influencia de la observación \(i\)-ésima sobre el valor ajustado (\(\hat{y}_{i}\)). Esta se calcula así:
\[ DFFITS_{i} = \frac{\hat{y}_{i} - \hat{y}_{(i)}}{\hat{\sigma}_{(i)}^{2}h_{ii}} = \sqrt{ \frac{h_{ii}}{1-h_{ii}} }t_{i}. \]
El \(DFFITS_{i}\) puede ser grande si el dato es atípico (\(t_{i}\) grande) o si el dato tiene gran balanceo (\(h_{ii}\) grande). Se sugiere que si \(|DFFITS_{(j,i)}| > 2\sqrt{p/n}\) es necesario examinar la \(i\)-ésima observación.
5.4.1.4 COVRATIO
Los diagnósticos anteriores permiten ver el efecto de las observaciones sobre \(\hat{\boldsymbol \beta}\) o \(\hat{\boldsymbol y}\). Pero no proporcionan información sobre la precisión general de la estimación. Una medida global de la precisión es la varianza generalizada:
\[ GV(\hat{\boldsymbol \beta}) = | Var(\hat {\boldsymbol \beta}) | = |\sigma^{2}(\boldsymbol X'\boldsymbol X)^{-1}|.\]
Para determinar la influencia de la \(i\)-ésima observación en la precisión de la estimación se define la razón de covarianzas:
\[ COVRATIO_{i} = \frac{|(\boldsymbol X'_{(i)}\boldsymbol X_{(i)})^{-1}\hat{\sigma}_{(i)}^{2}|}{| (\boldsymbol X'\boldsymbol X)^{-1}\hat{\sigma}^{2} |}= \left( \frac{S^{2}_{(i)}}{S^{2}} \right)^{p} \left( \frac{1}{1-h_{ii}} \right). \]
Si \(COVRATIO_{i} > 1 + 3p/n\) o \(COVRATIO_{i} > 1 - 3p/n\) se debería considerar a la \(i\)-ésima observación como influyente para la precisión de \(\widehat{\boldsymbol \beta}\).
Datos de la ONU - medidas de influencia
En R las medidas de influencia se pueden calcular usando la función influence.measures. Aunque también se pueden calcular cada indicador de forma independiente.
La distancia de Cook se observa en la Figura 5.7. Aquí vemos que Guinea Ecuatorial y Corea del Norte son los países que más influyen en las estimaciones de los parámetros del modelo. Lo demás países presentan valores de la distancia de Cook mucho más bajos. Note que aunque observamos que Trinidad y Tobago es un punto de balanceo, este país no es influyente (valor de la distancia de Cook de \(0.0082\)).
CD.UN11 = cooks.distance(mod.UN11)
OrderCD.UN11 = order(CD.UN11,decreasing = T)
plot(CD.UN11,type='h',ylab = 'distancia de Cook',xlab='índice')
text(OrderCD.UN11[1:2],CD.UN11[OrderCD.UN11[1:2]],Names[OrderCD.UN11[1:2]],pos=4,cex=0.6)
abline(h=4/199,lty=2)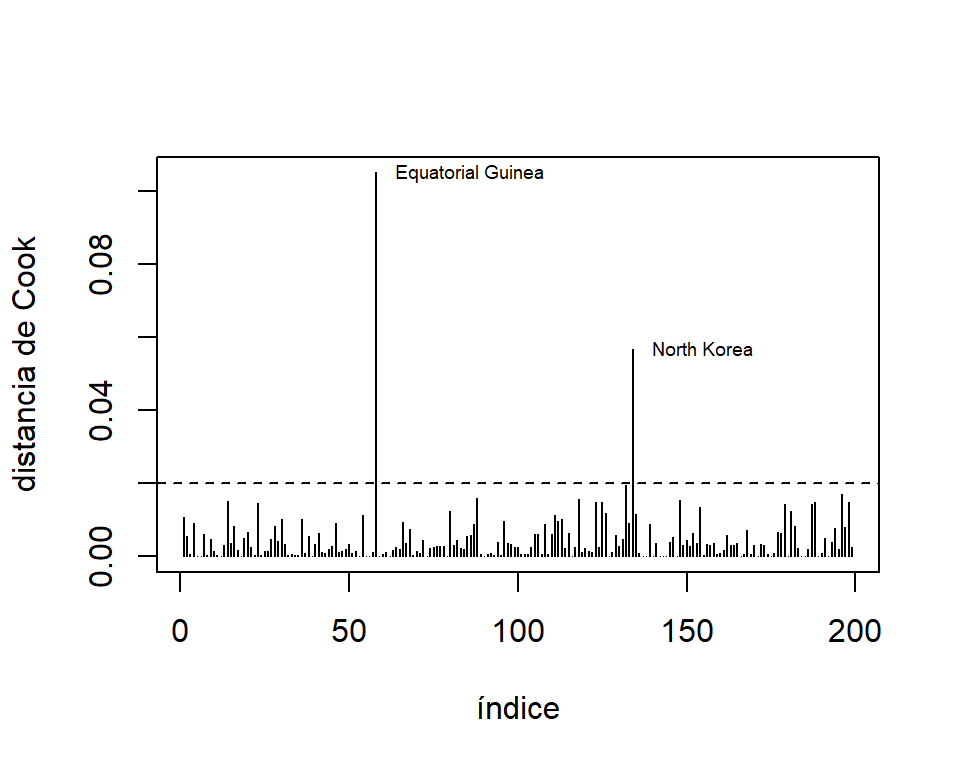
Figure 5.7: Datos de la ONU. Distancia de Cook.
Ya identificamos que Guinea Ecuatorial y Corea del Norte son influyentes y pueden afectar considerablemente las estimaciones de los coeficientes de regresión. Pero esta influencia puede ser solamente sobre algún o algunos parámetros. Para ver la influencia sobre cada parámetro, la Figura 5.8 muestra los DFBETAS para los coeficientes \(\beta_{1}\) y \(\beta_{2}\). En ambos gráficos podemos ver que estos dos países son influyentes para ambos parámetros. También se pude observar que otros pocos países tienen cierta influencia en la estimación de \(\beta_{2}\), aunque los valores de los DFBETAS están muy cerca de los puntos de corte.
DFBetas.UN11 = dfbetas(mod.UN11)
OrderDB1.UN11 = order(abs(DFBetas.UN11[,2]),decreasing = T)
OrderDB2.UN11 = order(abs(DFBetas.UN11[,3]),decreasing = T)
par(mfrow=c(1,2))
plot(DFBetas.UN11[,2],ylab=quote('DFBETA'~(beta[1])),xlab='índice',main='(a)')
text(OrderDB1.UN11[1:2],DFBetas.UN11[OrderDB1.UN11[1:2],2],
Names[OrderDB1.UN11[1:2]],pos=4,cex=0.6)
abline(h = c(-1,1)*2/sqrt(199),lty=2)
plot(DFBetas.UN11[,3],ylab = quote('DFBETA'~(beta[2])),xlab='índice',main='(b)')
text(OrderDB2.UN11[1:2],DFBetas.UN11[OrderDB2.UN11[1:2],3],
Names[OrderDB2.UN11[1:2]],pos=4,cex=0.6)
abline(h = c(-1,1)*2/sqrt(199),lty=2)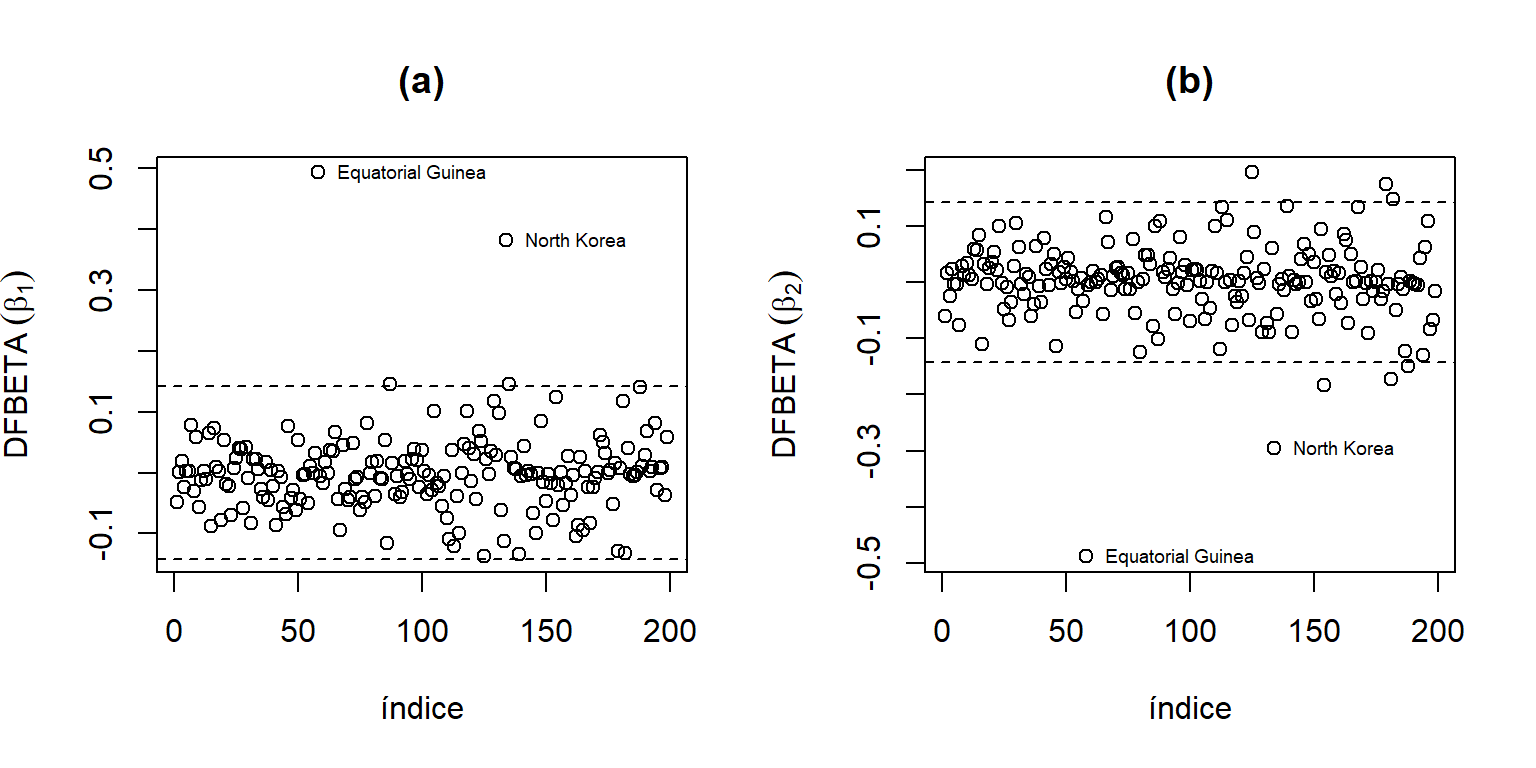
Figure 5.8: Datos de la ONU. DFBetas.
Los DFFITS y COVRATIO se observan en la Figura 5.9. A partir de los DFFITS se puede concluir que Guinea Ecuatorial y Corea del Norte también tienen gran influencia sobre las predicciones. A partir de los COVRATIO vemos que Trinidad y Tobago, Guinea Ecuatorial, Bosnia y Herzegovina, y Moldavia tienen gran influencia en la varianza de las estimaciones de los coeficientes de regresión. Note que aunque Corea del Norte fue influyente para las estimaciones, este país no influye en la varianza de estas.
DFfits.UN11 = dffits(mod.UN11)
OrderDFF.UN11 = order(abs(DFfits.UN11),decreasing = T)
Covratio.UN11 = covratio(mod.UN11)
OrderCR.UN11 = order(abs(1-Covratio.UN11),decreasing = T)
par(mfrow=c(1,2))
plot(DFfits.UN11,ylab='DFFITS',xlab='índice',main='(a)')
text(OrderDFF.UN11[1:2],DFfits.UN11[OrderDFF.UN11[1:2]],
Names[OrderDFF.UN11[1:2]],pos=4,cex=0.6)
abline(h = c(-1,1)*2*sqrt(3/199),lty=2)
plot(Covratio.UN11,ylab = 'COVRATIO',xlab='índice',main='(b)')
text(OrderCR.UN11[1:4],Covratio.UN11[OrderCR.UN11[1:4]],
Names[OrderCR.UN11[1:4]],pos=c(4,2,4,4),cex=0.6)
abline(h = 1+c(-1,1)*3*3/199,lty=2)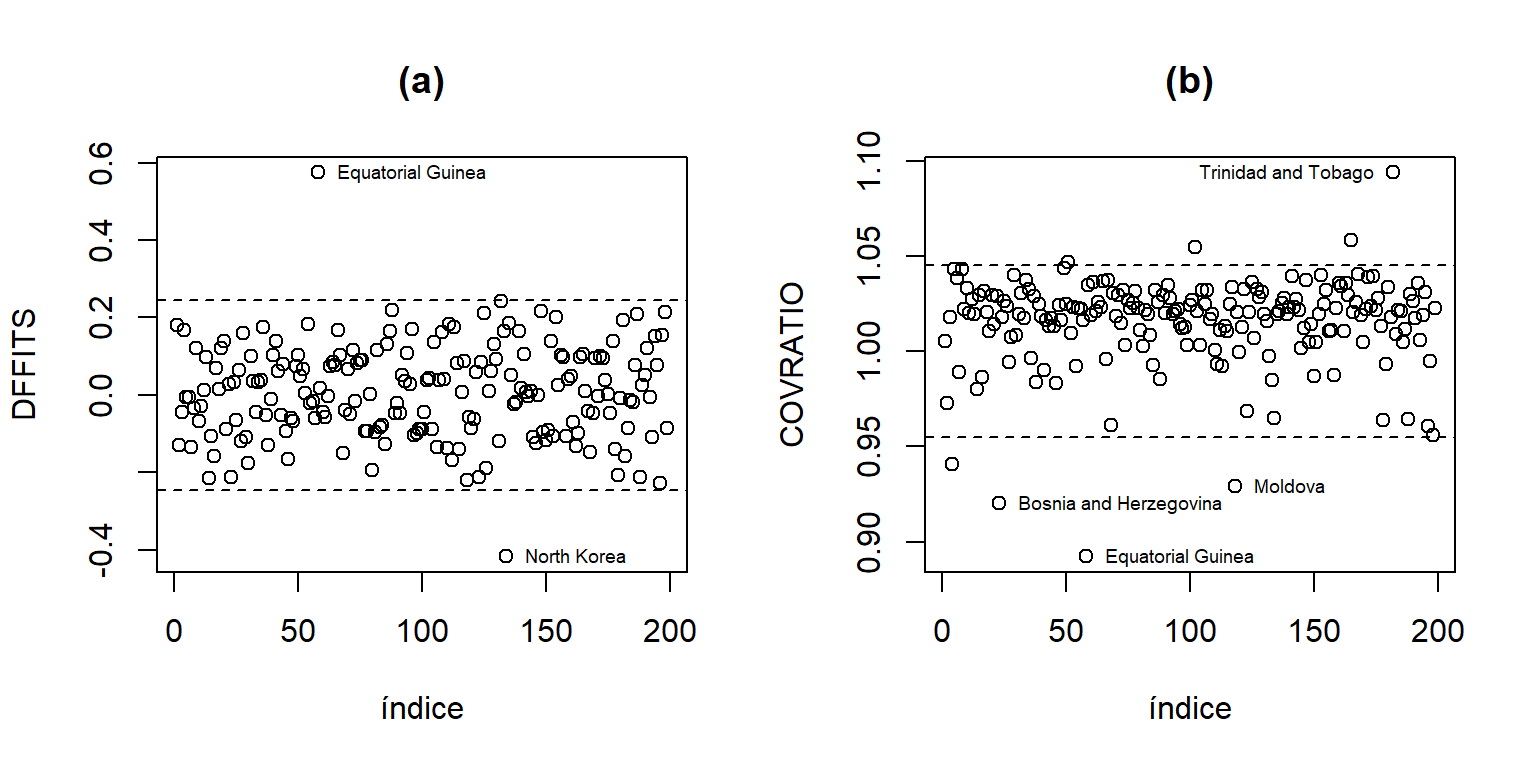
Figure 5.9: Datos de la ONU. DFFITS y COVRATIO.
A partir de estos indicadores encontramos que Guinea Ecuatorial y Corea del Norte son observaciones influyentes en la estimación del modelo (5.1). Particularmente, Guinea Ecuatorial tiene una tasa de fertilidad (4.98) muy superior a la estimada por el modelo. Esto se debe que los países con PNB y porcentaje de población urbana similares a este país tienen tasas de fertilidad más baja. Caso contrario pasa con Corea del Norte.
Para disminuir la influencia de estos países se pueden incorporar nuevas covariables dentro del modelo que ayuden a explicar estas discrepancias. Por ejemplo se podría ingresar una covariable asociada al continente.5.5 Comentarios finales
- Dentro de la literatura hay muchos puntos de corte diferentes para los indicadores de observaciones influyentes. Esto es porque es difícil de determinar las distribuciones muestrales. Por lo que se recomienda verificar si hay algunas observaciones que tenga valores muy altos con respecto a los demás.
- Las observaciones influyentes o atípicas se deben descartar si estas corresponden a errores de medición o si son inválidas (por ejemplo, si pertenecen a otra población).
- Pero si las observaciones influyentes o atípicas son válidas, no hay justificación para eliminarla. Lo que se puede hacer es incluir nuevas covariables que puedan explicar mejor los datos y reducir la influencia de estas observaciones. En los datos de la ONU podríamos incluir covariables relacionadas con el continente.